[ICML 2024] DSG: 基于球面高斯约束引导的条件扩散模型

本文介绍我们组发表在ICML 2024关于Diffusion Model的工作《Guidance with Spherical Gaussian Constraint for Conditional Diffusion》。本工作旨在利用预训练的扩散模型实现损失函数引导的、无需训练的条件生成任务。本工作上海科技大学2023级研究生杨凌霄为第一作者，由石野教授指导完成。

论文地址：

Guidance with Spherical Gaussian Constraint for Conditional Diffusion​arxiv.org/abs/2402.03201

代码链接：

摘要

最近的Guidance方法试图通过利用预训练的扩散模型实现损失函数引导的、无需训练的条件生成。虽然这些方法取得了一定的成功，但它们通常会损失生成样本的质量，并且只能使用较小的Guidance步长，从而导致较长的采样过程。

在本文中，我们揭示了导致这一现象的原因，即采样过程中的流形偏离（Manifold Deviation） 。我们通过建立引导过程中估计误差的下界，从理论上证明了流形偏离的存在。

为了解决这个问题，我们提出了基于球形高斯约束的Guidance方法（DSG），通过解决一个优化问题将Guidance步长约束在中间数据流形内，使得更大的引导步长可以被使用。

此外，我们提出了该DSG的闭式解（Closed-Form Solution）, 仅用几行代码，就能够使得DSG可以无缝地插入(Plug-and-Play)到现有的无需训练的条件扩散方法，在几乎不产生额外的计算开销的同时大幅改善了模型性能。我们在各个条件生成任务（Inpainting, Super Resolution, Gaussian Deblurring, Text-Segmentation Guidance, Style Guidance, Text-Style Guidance, and FaceID Guidance）中验证了DSG的有效性。

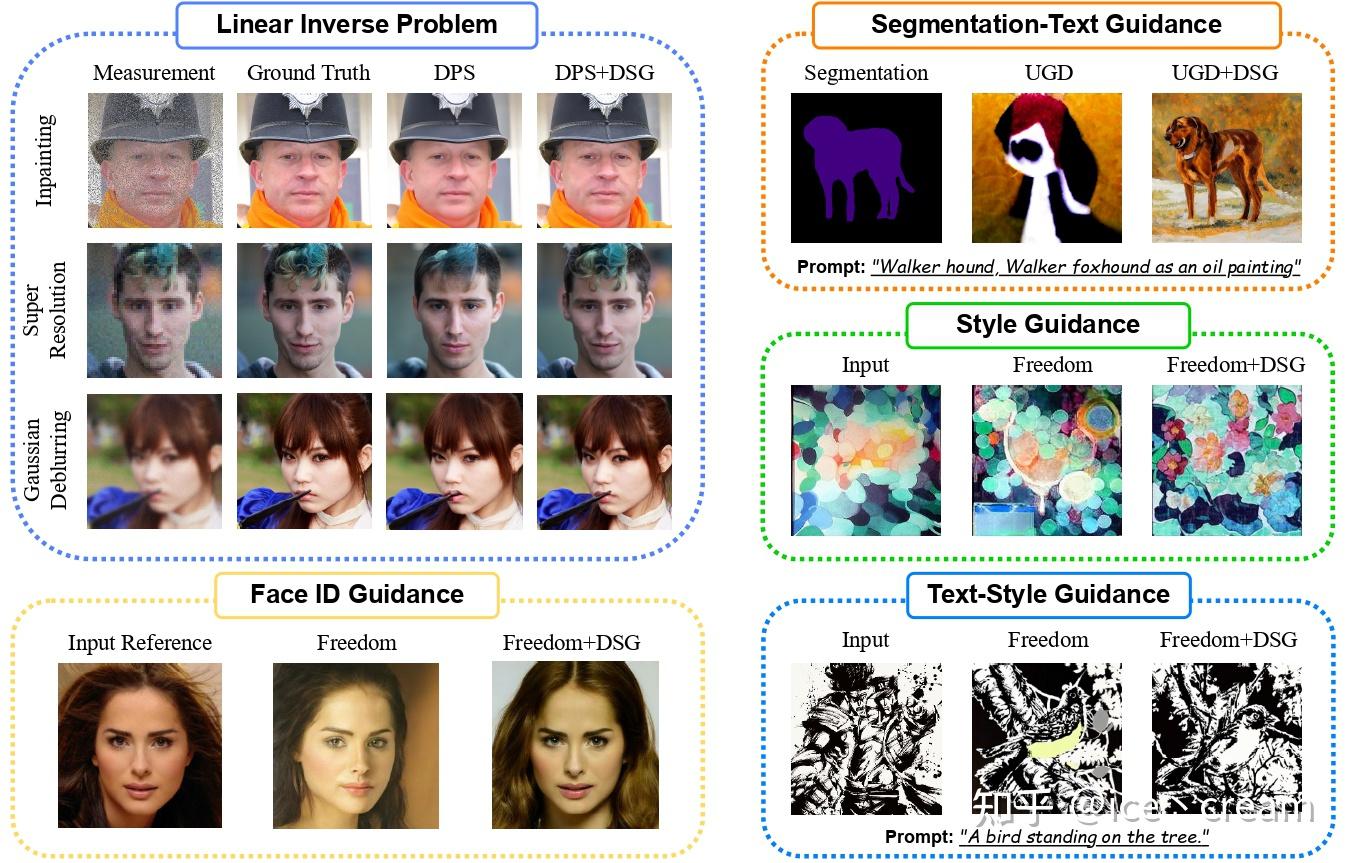
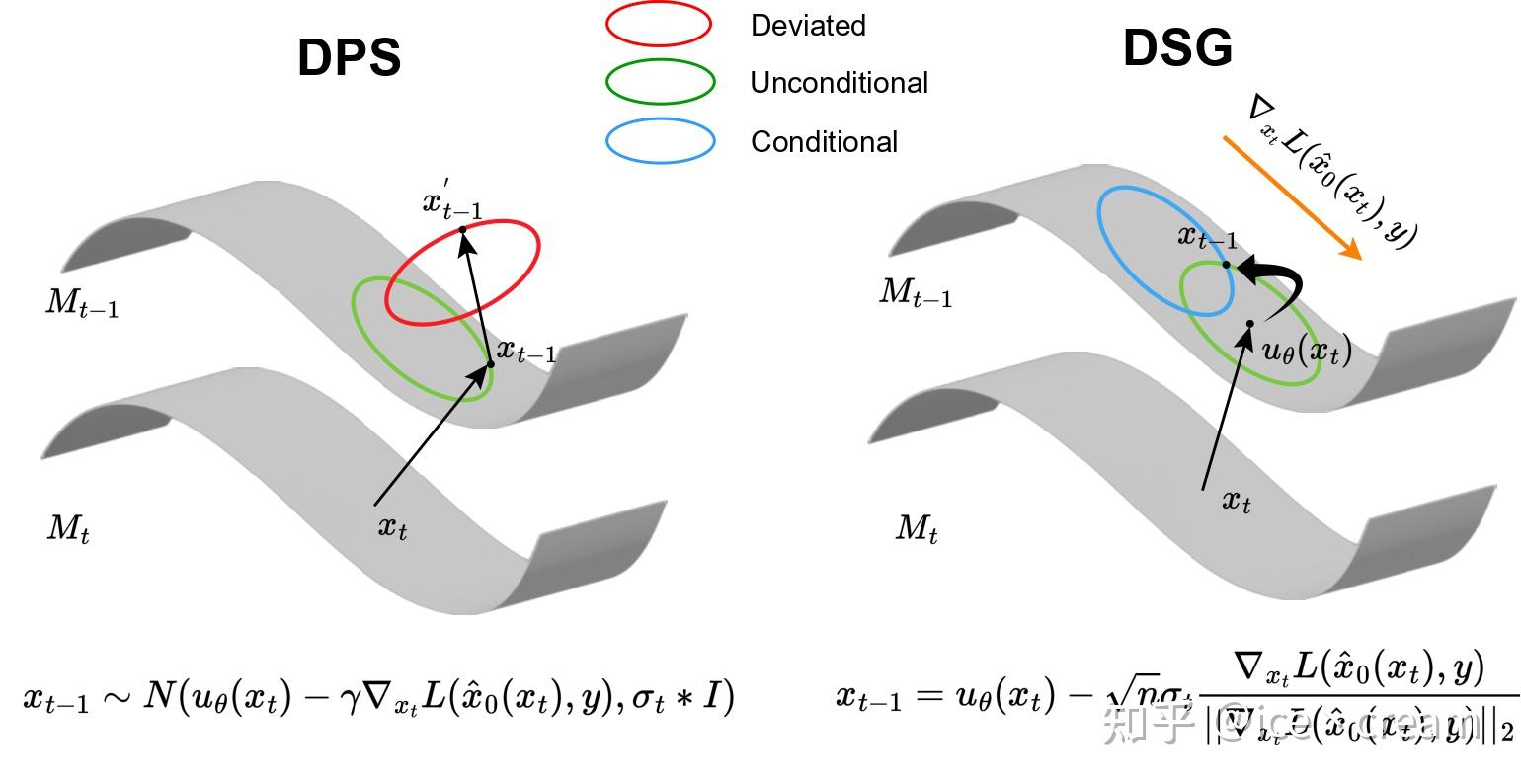
背景：无需训练的条件扩散模型

Classifier guidance首先提出使用预训练的扩散模型进行条件生成。它利用贝叶斯公式 $p(x|y)=p(y|x)p(x)/p(y)$p(x|y)=p(y|x)p(x)/p(y) ，通过引入额外的似然项 $p(x_t|y)$p(x_t | y) 来实现条件生成：

${\mathrm{\nabla }}_{x_t}\log p(x_t|y)={\mathrm{\nabla }}_{x_t}\log p(x_t)+{\mathrm{\nabla }}_{x_t}p(y|x_t),$\nabla_{x_t} \log p(x_t | y) = \nabla_{x_t} \log p(x_t) + \nabla_{x_t} p(y | x_t),

然而，这种方法需要训练一个time-dependent classifier来估计 ${\mathrm{\nabla }}_{x_t}p(y|x_t)$\nabla_{x_t} p(y | x_t) ，会造成额外的训练成本，如需要收集成对的数据(x,y)，需要精细地设计time-dependent classifier的网络结构，或是需要针对超参数进行额外的调参。Classifier-free guidance同样也用于条件生成，但是它在训练diffusion model的时候就加入了条件，也会导致上述的训练成本。

因此，目前无需训练的方法是基于Classifier guidance，将time-dependent classifier替换成某个定义在 $x_0$x_0 上的可微损失函数 $L(x_0,y)$L(x_0,y) ，并利用Tweedie's formula求解额外的似然项 ( 使用Tweedie's formula的原因是，损失函数 $L(x_0,y)$L(x_0,y) 是定义在干净的数据流形 $x_0$x_0 上的，直接将噪声数据 $x_t$x_t代入Loss并不make sense )：

$\begin{array}{rl}{\mathrm{\nabla }}_{x_t}\log p(y|x_t)& \approx {\mathrm{\nabla }}_{x_t}\log p(y|{\hat{x}}_0(x_t)),\\ & =\gamma {\mathrm{\nabla }}_{x_t}L({\hat{x}}_0(x_t),y)\end{array}$\begin{align} \nabla_{x_t} \log p(y | x_t) &\approx \nabla_{x_t} \log p(y | \hat{x}_0(x_t)), \\ &= \gamma \nabla_{x_t} L(\hat{x}_0(x_t),y) \end{align}

这里 $x_t\sim \mathcal{N}(a_t{x}_0,b_t^{2}I)$x_t \sim \mathcal{N}(a_t x_0, b_t^2 I) 表示加噪t步的data， $\gamma$\gamma 表示引导步长。因此，总体的采样过程可以被写成

$x_{t-1}=\underset{\text{sampling step}}{\underbrace{DDIM(x_t,{ϵ}_{\theta }(x_t,t))}}-\underset{\text{correction step}}{\underbrace{\gamma {\mathrm{\nabla }}_{x_t}L({\hat{x}}_0(x_t),y)}}.$x_{t-1} = \underbrace{DDIM(x_t, \epsilon_\theta(x_t,t))}_{\text{sampling step}} - \underbrace{\gamma \nabla_{x_t} L(\hat{x}_0(x_t),y)}_{\text{correction step}}.

因此，目前无需训练的方法只使用了pretrained unconditional diffusion model的知识，利用一个额外的损失函数 $L(x_0,y)$L(x_0,y) 就能够实现条件生成。

损失函数引导过程中的流形偏离（Manifold Deviation）

尽管先前的工作由于其灵活的特性在各种条件生成任务中取得了巨大成功，但它们会牺牲生成样本的质量。在本文中，我们提出这种现象产生的原因是线性流形假设（Linear Manifold Assumption）和Jensen Gap导致的流形偏离：

1. 线性流形假设：线性流形假设是一个相当强的假设，因此在实践中通常会引入误差。
2. Jensen Gap：在实际情况下， $p(x_0|x_t)$p(x_0 | x_t)​ 的分布是未知的，将其简单地用Tweedie’s formula的估计均值替代会引入Jensen Gap： $\mathcal{J}(f,x\sim p(x))=\mathbb{E}[f(x)]-f(\mathbb{E}[x])={\mathbb{E}}_{x_0|x_t}[L(x_0)]-L({\hat{x}}_0(x_t))$\mathcal{J}(f,x \sim p(x)) = \mathbb{E}[f(x)] - f(\mathbb{E}[x]) = \mathbb{E}_{x_0|x_t}\left[L(x_0)\right] - L(\hat{x}_0(x_t))

本文指出，即使DPS提供了Jensen Gap的上界，它仍然具有下界，也会引入估计误差：

$\mathcal{J}\ge \frac{1}{2}\beta \sum _{i=1}^n{\lambda }_i.$\mathcal{J} \ge \frac{1}{2}\beta \sum_{i=1}^n \lambda_i.

基于球面高斯约束引导的条件扩散模型（DSG）

既然无论Jensen Gap还是线性流形假设都会不可避免地引入估计误差，那么为什么不在已经无条件的中间数据流形（Intermediate Data Manifold）中，找到那个最接近条件采样的点呢？

因此，我们提出了DSG(Diffusion with Spherical Gaussian constraint),一种在无条件中间流形M_t的高置信区间内进行Guidance的优化方法：

$\begin{array}{rl}\underset{x^{\prime }}{\arg min}& {[{\mathrm{\nabla }}_{x_t}L({\hat{x}}_0(x_t),y)]}^T(x^{\prime }-x_t)\\ \text{s.t.}& x^{\prime }\in C{I}_{1-\delta }\end{array}$\begin{align} \mathop{\arg\min}\limits_{x'} & \left[\nabla_{x_t} L(\hat{x}_0(x_t),y)\right]^T (x'-x_t) \\ \text{s.t.}& \;x' \in CI_{1-\delta} \end{align}

这里 $C{I}_{1-\delta }$CI_{1-\delta} 表示高斯分布的概率为(1- $\delta$\delta)的置信区间。在这个优化问题中目标函数倾向于让采样过程在梯度下降方向进行，约束则是将采样约束在高斯分布的高置信区间。

然而，当高置信区间包含n维空间中时，优化问题就变得具有挑战性。幸运的是，高维各向同性高斯分布的高置信区间集中在一个超球上，我们可以通过用这个超球近似它来简化约束，称为球面高斯约束(Spherical Gaussian Constraint):

$\begin{array}{rl}\underset{x^{\prime }}{\arg min}& {[{\mathrm{\nabla }}_{x_t}L({\hat{x}}_0(x_t),y)]}^T(x^{\prime }-x_t)\\ \text{s.t.}& x^{\prime }\in S_{{\mu }_{\theta }(x_t),\sqrt{n}{\sigma }_t}^n\end{array}$\begin{align} \mathop{\arg\min}\limits_{x'} & \left[\nabla_{x_t} L(\hat{x}_0(x_t),y)\right]^T (x'-x_t) \\ \text{s.t.}& \;x' \in S^n_{\mu_\theta(x_t),\sqrt{n}\sigma_t} \end{align}

这里 $S_{\mu ,r}^n=S_{{\mu }_{\theta }(x_t),\sqrt{n}\sigma }^n=\{x\in {\mathbb{R}}^n:||x-{\mu }_{\theta }(x_t)|{|}_2^2=r^2=n{\sigma }_t^2\}$S^n_{\mu,r}=S^n_{\mu_\theta(x_t),\sqrt{n}\sigma}=\{x \in \mathbb{R}^n: ||x-\mu_\theta(x_t)||_2^2= r^2=n \sigma_t^2 \} 表示n维高斯分布近似的超球。通过这种近似方法，我们能够得到优化问题的闭式解：

$x_{t-1}^{\ast }={\mu }_{\theta }(x_t)-\sqrt{n}{\sigma }_t\frac{{\mathrm{\nabla }}_{x_t}L({\hat{x}}_0(x_t),y)}{||{\mathrm{\nabla }}_{x_t}L({\hat{x}}_0(x_t),y)|{|}_2}.$x^*_{t-1} = \mu_\theta(x_t) - \sqrt{n}\sigma_t \frac{\nabla_{x_t} L(\hat{x}_0(x_t),y)}{||\nabla_{x_t} L(\hat{x}_0(x_t),y)||_2}.

这个闭式解的求得能够表明，DSG可以无缝插入目前的无需训练的条件扩散模型，如DPS、Freedom、UGD，而不造成额外的计算复杂度。并且，只需要修改几行代码就能够产生更好的样本和达到更快的推理速度。

另外，从另一个角度看，DSG也可以看成在预测均值 ${\mu }_{\theta }(x_t)$\mu_\theta (x_t) 上进行梯度下降。而且，由于 ${\sigma }_t$\sigma_t 与 $t$t 正相关，DSG可以看作是自适应的梯度下降方法，在一开始下降步长大，在最后下降步长小。在实验中，我们发现DSG最大的步长能够达到DPS的400倍，因此能够在更小的DDIM steps下相比于DPS更加鲁棒。

此外，我们发现DSG虽然增强了对齐能力和真实性，但是在多样性方面有所损失。因此，我们对原始采样方向和梯度下降方向的进行加权，就像Classifier-free Guidance那样:

$d_m=d^{sample}+g_r(d^{\ast }-d^{sample}).$d_m = d^{sample} + g_r(d^*-d^{sample}).

$x_{t-1}={\mu }_{\theta }(x_t)+r\frac{d_m}{||d_m||}.$x_{t-1} = \mu_\theta (x_t) + r \frac{d_m}{||d_m||}.

这里 $d^{sample}={\sigma }_t{ϵ}_t$d^{sample}=\sigma_t \epsilon_t 表示无条件采样方向， $d^{\ast }=-\sqrt{n}{\sigma }_t\cdot \frac{{\mathrm{\nabla }}_{x_t}L({\hat{x}}_0(x_t),y)}{||{\mathrm{\nabla }}_{x_t}L({\hat{x}}_0(x_t),y)||}$d^*=- \sqrt{n}\sigma_t \cdot \frac{\nabla_{x_t}L(\hat{x}_0(x_t),y)}{||\nabla_{x_t}L(\hat{x}_0(x_t),y)||} 表示最速梯度下降方向。另外， $d_m$d_m 会被缩放以满足球面高斯约束。

算法流程图如下：

实验结果

我们验证了DSG在各个任务上的性能都能够显著地超过baseline。

Linear Inverse Problems in FFHQ with DDIM steps=1000

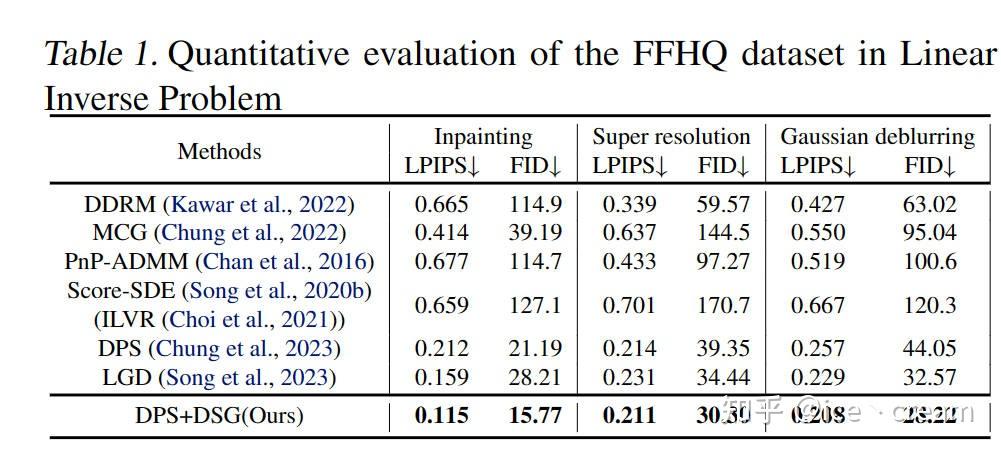
Linear Inverse Problems in FFHQ with DDIM steps=100,50,20

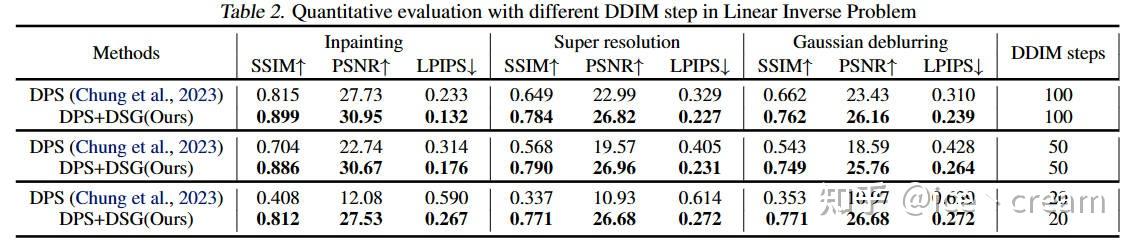
可以看到，DPS+DSG在DDIM steps=1000,100,50,20都远超DPS，并且在DDIM steps较小的时候能够观察到与DPS更大的性能差距。这种现象可归因于DPS的局限性，即为了不远离流形使用的小步长。因此，随着guidance步数的减少，测量结果的对齐变得越来越具有挑战性。相比之下，我们的模型在性能上只有轻微的下降。这是因为DSG允许更大的步长，同时仍然保留在中间流形上。因此，即使减少了去噪步骤，我们仍然可以在生成真实样本的同时实现与测量结果的精确对齐，如图6所示。

FaceID Guidance in Celeba-HQ

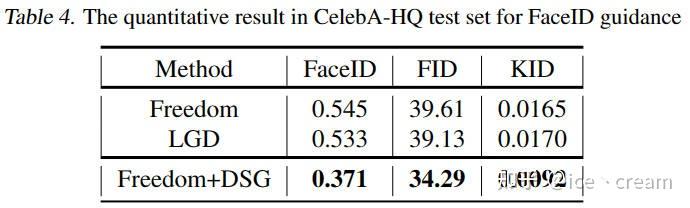
Style Guidance

Text-Style Guidance

Other Tasks

由于篇幅限制，更多实验结果、实验设置请查看原文以获取更多细节。

总结

在本文中，我们揭示了无需训练的条件扩散模型中的一个关键问题：在使用基于损失函数的引导时，在采样过程中会出现流形偏移现象。为解决这一问题，我们提出了一种 基于球面高斯约束引导的条件扩散（DSG）方法，灵感来源于高维高斯分布中的集中现象。DSG通过优化有效地限制引导步骤在中间数据流形内，从而减轻流形偏移问题，并能够使用更大的引导步长。此外，我们为基于球形高斯约束的DSG去噪过程提供了一个封闭形式的解决方案。值得注意的是，DSG可以作为一个即插即用的模块，用于无需训练的条件扩散模型（CDM）。将DSG整合到这些CDM中，仅涉及修改几行代码，几乎不增加额外的计算成本，但却显著提高了性能。我们已将DSG整合到几个最新的CDM中，用于各种条件生成任务。实验结果验证了DSG在样本质量和时间效率方面的优越性和适应性。