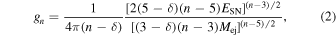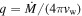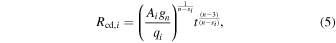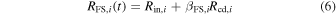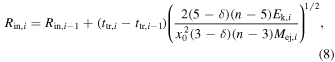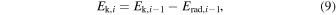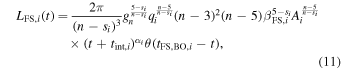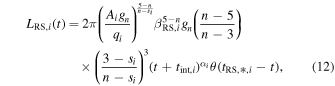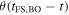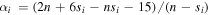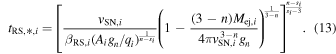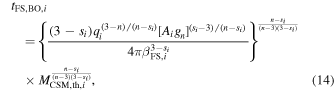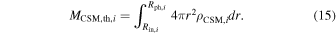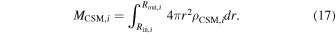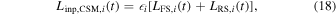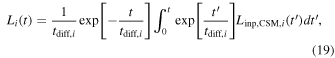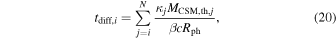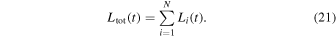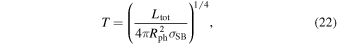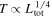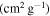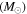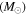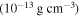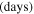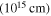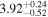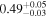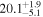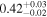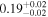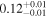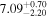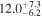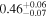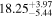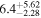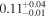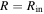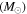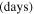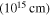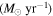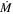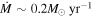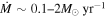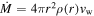多重喷射星周介质相互作用模型及其对超亮超新星iPTF15esb和iPTF13dcc的影响

在过去的十年中，快速发展的非目标超新星（SN）勘测计划发现了一类新的不寻常的SNe，其峰值绝对星等为M_峰亮度大于−21等。这些非常明亮的SNe被称为超亮超新星（SLSNe）;Quimby 等人，2011 年;Gal-Yam 2012 年）。

看来，SLSNe可以简单地分为两个亚类，即I型和II型。SLSNe I 在缺乏氢吸收线的峰周围有光谱，它们的光曲线 （LC） 可能由对不稳定性 SNe 解释（Rakavy & Shaviv 1967;Heger & Woosley 2002;Heger et al. 2003），⁵⁶镍动力模型，磁星动力模型（Kasen & Bildsten 2010;伍斯利 2010;Inserra 等人，2013 年;Wang et al. 2015a， 2015b， 2016a;Dai 等人，2016 年;Liu 等人，2017 年;Yu et al. 2017），或喷射物-星周介质（CSM）相互作用模型（Chevalier & Irwin 2011;Chatzopoulos 等人，2012 年，2013 年;金茨堡和巴尔伯格 2012;Nicholl 等人，2014 年;Chen 等人，2015 年）。

另一方面，SLSNe II峰周围的光谱显示出较强的氢发射特征，并且几乎所有峰都显示出窄和中等宽度的Balmer发射线，与正常的SNe IIn相似。以前的研究（Smith & McCray 2007;Moriya 等人，2011 年，2013 年;Chatzopoulos et al. 2012， 2013）认为，SLSNe IIn的LCs可能由SN喷射物与致密、富氢和光学厚的CSM之间的相互作用提供动力。

然而，一些SLSNe I（例如，iPTF13ehe、iPTF15esb和iPTF16bad）的晚期光谱显示Hα发射线（Yan等人，2015,2017）使分类方案复杂化。 Yan等人（2015）估计，15%的SLSNe I可能具有这些光谱特征。在这些具有晚期Hα发射谱线的SLSNe I中，iPTF15esb以0.224的红移z爆炸，是最引人注目的。其后期光谱显示强而宽的Hα发射线，表明SN喷射物与SN祖细胞周围的富氢CSM壳层之间的相互作用。此外，其LC有两个峰，其光度彼此大致相等（L_峰≈ 4 × 10⁴³ERG S⁻¹）和持续约40天的平台期。其后期 LC 衰减为 L_波尔∝ 吨^−2.5.另一个有趣的案例是 iPTF13dcc（Vreeswijk 等人，2017 年），其 LC 显示初始缓慢下降，持续时间为 ∼30 天，然后重新变亮并达到第二个峰值。

iPTF15esb 和 iPTF13dcc 的 LC 都挑战了上述所有模型。由⁵⁶完全捕获γ射线的Ni级联衰变为每天0.0098等，由磁星驱动的晚期LC（完全捕获γ射线）可以用L来描述_inp，mag∝ 吨⁻².磁星模型，以及⁵⁶镍级联衰变伴γ射线泄漏（Clocchiatti & Wheeler 1997;Chen 等人，2015 年;Wang等人，2015a）能够解释iPTF15esb的晚期LC，但该模型无法产生显示两个明亮峰和一个平台的LC。似乎需要一个涉及多次能量注入的能量源模型来解释iPTF15esb的奇异LC。Wang等人（2016b）提出了一个三重能源模型（⁵⁶Ni加磁星加相互作用），并用它来解释iPTF13ehe的LC。然而，该模型仅涉及喷射物和 CSM 壳之间的一次碰撞，并且不能产生波动的 LC。Vreeswijk等人（2017）采用的包含冷却发射和磁星自旋或喷射-CSM相互作用的模型来拟合iPTF13dcc的双峰LC，还不能重现iPTF15esb的LC中看到的波动。

然而，正如Yan等人（2017）所指出的那样，光谱和LC似乎有利于SN喷射物与不同半径的多个CSM壳或CSM团块之间的相互作用。在这里，我们提出了一个涉及SN喷射与多个壳层和恒星风之间相互作用的喷射-CSM相互作用模型，并使用该模型拟合iPTF15esb的LC。双重相互作用模型也有望解释iPTF13dcc的LC。

本文的结构如下。在第 2 节中，我们详细介绍了该模型，并将其应用于第 3 节中 iPTF15esb 和 iPTF13dcc 的 LC。最后，我们讨论了我们的结果，并在第4节中提出了我们的结论。

在本节中，我们将正常的喷射物-CSM相互作用模型推广为涉及多个CSM壳和风的更复杂的模型。该模型的基本物理情况如下所述。喷射物与预先存在的CSM的相互作用导致形成两种冲击波：通过CSM传播的前向激波（FS）和扫过SN喷射物的反向激波（RS）（Chevalier 1982;Chevalier&Fransson，1994年）。这种相互作用通过将动能转化为辐射来提供强大的能量来源。

基于SN爆炸的数值模拟，可以采用SN喷射密度的破幂律分布（Matzner&McKee 1999）。外部喷射物的密度分布为

其中 n 是外侧喷射物的斜率，取决于 SN 祖星，g_n是密度分布缩放参数，由（Chevalier & Fransson 1994;Chatzopoulos 等人，2012 年)

where δ is the inner density profile slope. Here, E_SN is the total SN energy, and M_ej is the total mass of the SN ejecta. The relation between E_SN and M_ej can be written as (Chatzopoulos et al. 2012)

where x₀ denotes the dimensionless radius of a break in the supernova ejecta density profile from the inner component to the outer component.

Before the SN explosion, the mass loss of a massive star could erupt several gas shells surrounding the progenitor. We assume that the density of a circumstellar shell or wind is

where q_i is a scaling constant, and s_i is the power-law index for a CSM density profile and therefore s_i = 2 indicates stellar winds, while s_i = 0 indicates uniform density shells. The subscript "i" denotes the ith collision between the ejecta and the CSM shell. For a steady wind (s_i = 2) with a constant pre-explosion mass loss rate and wind velocity v_w, we have .

The shocked CSM and shocked ejecta are separated by a contact discontinuity. The radius of the contact discontinuity R_cd can be described by a self-similar solution (Chevalier 1982)

where A_i is a constant. The radii of the FS and RS are given by

and

where R_in,i is the initial radius of the ith interaction (which is equal to the inner radius of the CSM density profile), β_FS and β_RS are constants representing the ratio of the shock radii to the contact-discontinuity radius R_cd. The values of β_FS and β_RS are determined by the values of n and s_i. They are given in Table 1 of Chevalier (1982). For n = 7 and s_i = 2, we can obtain β_FS = 1.299, β_RS = 0.970, and A = 0.27; for n = 7 and s_i = 0, we have β_FS = 1.181, β_RS = 0.935, and A = 1.2.

The interaction radii that are equal to the inner radii of the CSM density profile are given by

where t_tr,i is the trigger time of the ith interaction relative to the time zero-point. Here, we set the first interaction between ejecta and the CSM as the time zero-point. The kinetic energy of the ith interaction is

where E_rad is the energy loss due to radiation. The ejecta mass of the ith interaction is

The interaction between the ejecta and the CSM would convert the kinetic energy to radiation. The luminosity input function of the FS is (Chatzopoulos et al. 2012)

while the RS's input luminosity is (Wang et al. 2017)⁶

where and represent the Heaviside step function that controls the end times of FS and RS, respectively, and t_int,i ≈ R_in,i/v_SN,i is the time when the ejecta-CSM interaction begins. The temporal index is . Here, we fix n = 7. Consequently, we have α_i = −0.143 for the shell (s_i = 0), and α_i = −0.6 for the steady wind (s_i = 2).

The RS termination timescale t_RS,* is the time once the RS sweeps up all available ejecta (Chatzopoulos et al. 2012, 2013)

Under the same assumption, the FS terminates when the optically thick part of the CSM is swept up. The termination timescale of the FS, being approximately equal to the time of FS breakout t_FS,BO, is given by (Chatzopoulos et al. 2012, 2013)

where M_CSM,th,i is the mass of the optically thick CSM

Here, R_ph,i denotes the photospheric radius of the ith CSM shell, located at the optical depth τ = 2/3 under Eddington's approximation. R_ph,i is given by

where κ is the optical opacity of the CSM and R_out,i is the radius of the outer boundary of the CSM. R_out,i can be determined by

Both the FS and the RS heat the interacting material. The total luminosity input from the FS and RS can be written as

where _i is the conversion efficiency from the kinetic energy. Chatzopoulos et al. (2012) assumed that  = 100%, which is unrealistic in the actual situation, especially in the M_CSM ≪ M_ej case. Due to poor knowledge of the process of converting the kinetic energy to radiation, for simplicity, we set _i as a free parameter.

Because the expansion velocity of the CSM is much lower than the typical velocity of the SN ejecta, Chatzopoulos et al. (2012) assumed a fixed photosphere inside the CSM. Under this assumption, the output bolometric LC can be written as

where t_diff,i is the diffusion timescale in the optically thick CSM. The diffusion timescales of the ith interaction can be written as

where β = 4π³/9 ≃ 13.8 is a constant (Arnett 1982), and c is the speed of light.

In this multiple-interaction model, the theoretical bolometric LC of N times interactions can be described as

We assume that the bolometric luminosity comes from the blackbody emission from the photosphere whose radius is R_ph, and therefore the temperature in our model can be estimated by

where σ_SB is the Stefan–Boltzmann constant. By assuming a stationary photosphere, we have .

In this section, we use the model described above to fit the bolometric LCs of iPTF15esb and iPTF13dcc. In order to derive the best-fitting parameters and determine the ranges of relevant parameters, we develop a Markov Chain Monte Carlo method that can minimize the values of χ² divided by the number of degrees of freedom (χ²/dof) for the multiple ejecta-CSM interaction model, and adopt this model to fit the LCs of iPTF15esb and iPTF13dcc.

To reduce the number of free parameters in our calculations, we fix several parameters. We adopt the power-law index of the outer density profile n = 7 as an approximation for Type I SNe (Chevalier 1982), and the inner density slope δ = 0.

The free parameters in our model are the opacities of the CSM shells and winds κ, the mass of the SN ejecta M_ej, the total mass of the CSM M_CSM, the density of the CSM at the interaction radius ρ_CSM,in, the interaction radius (the inner radius of CSM) R_in, the conversion efficiency from the kinetic energy to radiation , the time of the collision between the SN ejecta and the CSM shells t_tr.

The opacities of the CSM shells and winds κ are related to their composition and temperatures. For hydrogen-poor matter, the dominant source of opacity is electron scattering, κ = 0.06–0.2 cm² g⁻¹ (see the references listed in Wang et al. 2015b). For hydrogen-rich matter, κ = 0.33 cm² g⁻¹, which is the Thomson electron scattering opacity for fully ionized material with the solar metallicity (Moriya et al. 2011; Chatzopoulos et al. 2012).

3.1. iPTF15esb

It is reasonable to assume that there are at least three collisions between the SN ejecta and the CSM shells, since the LC of iPTF15esb shows two prominent peaks and a plateau. In this scenario, the interaction between the SN ejecta and the stellar wind (i.e., s₁ = 2) powers the first peak of the LC of iPTF15esb, while the second peak and the plateau are powered by the interactions between the SN ejecta and CSM shells (s₂ = s₃ = 0) at different radii.

The composition of the first and second CSM shells cannot be well constrained, since no hydrogen emission lines in the early-time spectra of iPTF15esb have been detected. On the other hand, the strong, broad Hα emission at ∼70 days after the first LC peak might be prompted by the interaction between the ejecta and a hydrogen-rich shell. Therefore, the values of the opacity of the first and second CSM shells κ₁ and κ₂ can be fixed to be 0.06–0.2 or 0.33 cm² g⁻¹, and the value of the opacity of the third CSM shell κ₃ is supposed to be 0.33 cm² g⁻¹. By analyzing the Fe ii 5169 Å line, Yan et al. (2017) found that the photospheric velocity around the first peak of iPTF15esb is v_ph ≈ 17,800 km s⁻¹ which can be set to be the value of the characteristic velocity v_SN of the SN ejecta.

The theoretical LC of iPTF15esb is shown in Figure 1. The best-fitting parameters and the corresponding confidence contour corners of iPTF15esb are shown in Table 1 and Figure 2, respectively. We find that the multiple-interaction model can explain the bumpy LC of iPTF15esb well (χ²/dof = 1.71) and the parameters are reasonable. The derived physical parameters of the CSM shells and the wind are listed in Table 2. The masses of the optically thick part of the CSM shells M_CSM,th, which are close to their total mass, can be calculated. The termination timescales of the FS and the RS can also be determined. The optical depth of CSM τ_CSM > 1, indicating that these shells are opaque.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Table 1.  The Fitting Parameters for iPTF15esb and iPTF13dcc

	ith	s	κ	Mej	MCSM	ρCSM,ina	b	ttr	Rin
	Interaction
iPTF15esb
	1	2	0.2					−8.5
	2	0	0.2	4.41c				5.2	2.11d
	3	0	0.33	5.87c				24.2	5.15d
iPTF13dcc
	1	0	0.2					−73.79
	2	0	0.2	21.31c				−24.69	6.85d

Notes.

^aρ_CSM,in is the density of the CSM at radius . ^b is the conversion efficiency from the kinetic energy to radiation. ^cM_ej,2 and M_ej,3 are not fitting parameters, but were calculated by Equation (10). ^dR_in,2 and R_in,3 are not fitting parameters, but were calculated by Equation (8).

Download table as:  ASCIITypeset image

Table 2.  The Derived Physical Parameters

	ith Interaction	MCSM,tha	tFS,BO	tRS,*	tdiff	τCSMb	Rout	teruptc
iPTF15esb
	1	0.47	9.53	178.7	10.0	78.8	0.97	...	0.19–1.9
	2	1.35	16.8	39.7	9.0	10.1	2.25	6.69	...d
	3	1.77	39.6	120.0	6.2	4.1	5.5	16.34	...d
iPTF13dcc
	1	7.04	12.7	29.6	38.9	225.5	1.42	1.55	...d
	2	17.23	25.5	44.67	27.6	12.14	6.94	21.72	...d

Notes.

^aM_CSM,th is the mass of the optically thick CSM. ^bτ_CSM is the optical depth of the CSM. ^ct_erupt is the time of the progenitor star erupting the CSM shells before explosion. Here, we assume the velocity of the progenitor wind v_w = 100–1,000 km s⁻¹ and the shell expansion velocities v_shell = 100 km s⁻¹. ^dThe shells were promptly expelled by some instability process and their mass-loss rates cannot be calculated.

Download table as:  ASCIITypeset image

Provided that the velocity of the shells v_shell is ∼100 km s⁻¹ and using t_shell ≈ R_in/v_shell, we can obtain the time when the progenitor expelled the CSM shells before explosion. We infer that the progenitor of iPTF15esb has undergone at least two violent shell eruption processes at 6.69 and 16.34 years before the SN explosion, respectively, then experienced a wind-like mass loss whose mass-loss rate () is 0.19–1.9 M_⊙ yr⁻¹.⁷

3.2. iPTF13dcc

Vreeswijk et al. (2017) used a model combining the cooling emission from a shock-heated extended envelope (Piro 2015) and energy injection from a magnetar or an ejecta-CSM interaction to fit the LC of iPTF13dcc. While this model is plausible, we suggest that the double-collision model is also a possible model that can account for the LC of iPTF13dcc. In our scenario, the early-time bump of iPTF13dcc might be powered by the first collision between the ejecta and the CSM shell, while the second collision at a larger radius powers the late-time rebrightening of iPTF13dcc.

The early bump and the late-time rebrightening of iPTF13dcc are powered by the interactions between the SN ejecta and CSM shells at different radii, in which s₁ = s₂ = 0 is adopted. In our fitting, we adopt the expansion velocity v_SN = 10,000 km s⁻¹, which is the same as Vreeswijk et al. (2017). We assume the opacities of the first and second CSM shells κ₁ = κ₂ = 0.2 cm² g⁻¹.

The theoretical LC of iPTF13dcc is shown in Figure 3. The best-fitting parameters and the corresponding confidence contour corners of iPTF13dcc are shown in Table 1 and Figure 4, respectively. The multiple-collision model can match the unusual light curve of iPTF13dcc (χ²/dof = 2.25). The ejecta mass is M_ej = 14.2M_⊙, and the masses of CSM shells associated with the first and second collisions are 7.1M_⊙ and 18.3 M_⊙, respectively. Adopting t_shell ≈ R_in/v_shell and v_shell ∼ 100 km s⁻¹, we can infer that the two shells had been expelled at 1.55 and 21.72 years before the explosion, respectively.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Due to the lack of data before the maximum brightness of the early bump of iPTF13dcc, it is difficult to determine the rise time of the first bump. Based on Table 2 and Figure 3, we find that the rise time of the early bump depends on the forward-shock termination timescale of the first interaction t_FS,BO = 17.8 days, while the decline rate of the late-time LC is determined by the RS of the second collision.

3.3. The Factors Influencing the LC Features

Massive stars could be unstable and experience mass losses in the form of eruptions in the final stage of their lives (see, Smith 2014 and the references therein). Ofek et al. (2014) pointed out that more than 50% of the progenitors of type IIn SNe have experienced at least one pre-explosion eruption. In several cases, the progenitors of SNe could expel at least two shells and/or winds. Thus, it is expected that the interactions between the ejecta and multiple shells/winds would power bumpy LCs showing two or more peaks.

In this paper, we have studied two such bumpy SNe, iPTF15esb and iPTF13dcc, which show the undulation features that clearly deviate from the smooth rising and fading. The LC of iPTF15esb has two peaks and a post-peak plateau, while the LC of iPTF13dcc shows an early-time bump and a late-time rebrightening. All the previous energy-source models cannot account for these exotic features. We suggested that the LC undulations of iPTF15esb could arise from SN ejecta interacting with multiple dense CSM shells, which may be expelled by the eruptions of the progenitors. The interaction model for the LC of iPTF15esb is also favored by the broad Hα emission lines in the late-time spectra, which might be produced by the interaction of SN ejecta with a hydrogen-rich CSM shell located at a large distance from the progenitor star and was ejected by the progenitor star about 16.4 years before explosion.

To solve these problems, we generalize the "single" ejecta-CSM interaction model to the multiple-interaction model involving multiple CSM shells and/or winds. By employing this new model to fit the LC of iPTF15esb, we achieved rather good results and found that the first peak of the LC of iPTF15esb might be powered by the interaction between the SN ejecta and stellar wind, while both the second peak and the plateau might be powered by the two CSM shells at different radii. By fitting the LC, we found that the masses expelled by the progenitor of iPTF15esb are 0.49 and 1.46 M_⊙ and that the mass-loss rate () of the wind is 0.19–1.9 M_⊙ yr⁻¹, which is comparable to that of SN 1994W (, Chugai et al. 2004), SN 1995G (, Chugai & Danziger 2003), and iPTF13z (, Nyholm et al. 2017).

Furthermore, we also fitted the observed double-peaked LC of iPTF13dcc using this model and got rather satisfactory results. In this fit, the LC of iPTF13dcc was powered by the interactions between the ejecta and two CSM shells whose masses are 18.3 and 7.1 M_⊙, respectively. This positive result suggests that this model is also promising to account for the LCs of several double-peak SLSNe/SNe (e.g., Nicholl et al. 2016; Roy et al. 2016; Vreeswijk et al. 2017).

It is necessary to discuss the origins of the shells expelled by the progenitors of iPTF15esb and iPTF13dcc. Several models have been proposed to explain the violent pre-supernova eruptions. Woosley et al. (2007) and Woosley (2017) suggested that a very massive progenitor may undergo several episodes of pulsational pair instabilities and eject several massive shells before the SN explosion. The second possible origin is related to the binary interaction in which the shells ejected by the progenitor are supposedly formed by the large mass ejections from the progenitor interacting with its companion star (Podsiadlowski et al. 1992). In these successive collisions, the masses of the CSM shells decrease from the outermost shell (the first eruption) to the innermost shells (the final eruption), but their density increases (since the densities of the interiors of the progenitors are larger than that of the exterior). This property is consistent with the variation trend of our inferred densities of the ejected shells and the winds of the progenitors of iPTF15esb and iPTF13dcc.

The mass loss of the progenitor of an SN is an important process of stellar evolution. However, our understanding of the stellar mass loss mechanism remains incomplete. Further investigations for SLSNe/SNe like iPTF15esb and iPTF13dcc should shed light on the nature of the mass-loss histories of their progenitors.

We thank the anonymous referee for constructive suggestions that have allowed us to improve our manuscript significantly. We also thank Hai Yu, Weikang Zheng, Bing Zhang, Can-Min Deng, and Xue-Feng Wu for helpful discussions. This work was supported by the National Basic Research Program ("973" Program) of China (grant No. 2014CB845800), the National Key Research and Development Program of China (grant No. 2017YFA0402600), and the National Natural Science Foundation of China (grant No. 11573014). L.J.W. was also supported by the National Program on Key Research and Development Project of China (grant no. 2016YFA0400801). L.D.L. and S.Q.W. are supported by the China Scholarship Program to conduct research at UNLV and UCB, respectively.