利用基于子图的图注意网络解密单细胞分辨率下的空间转录组学细胞间通讯

细胞间通讯 （CCC） 是一个基本的生物过程，在免疫合作、器官发育、干细胞生态位和其他生物现象中起着至关重要的作用 ^1,2,3。单细胞转录组学的进步，尤其是单细胞 RNA 测序 （scRNA-seq），彻底改变了单个细胞的研究，为了解其组成、功能和动力学提供了前所未有的见解⁴。已经开发了 CellPhoneDB⁵、CellChat⁶、NicheNet⁷、CytoTalk⁸、scTensor⁹、iTALK¹⁰、ICELLNET¹¹、SingleCellSignalR¹² 和 Scriabin¹³ 等计算工具来推断和破译 CCC 网络¹⁴.例如，CellPhoneDB 和 CellChat 等工具提供了对配体-受体相互作用 （LRI） 的深入见解，这对于理解不同细胞类型的信号转导至关重要。这些工具采用创新方法和统计测试来量化每次相互作用的概率，有助于评估零假设和推断细胞间通讯中涉及的特定细胞类型。此外，NicheNet 和 CytoTalk 揭示了细胞内响应外部刺激的复杂基因-基因相互作用，而 scTensor 则采用超图来揭示高阶细胞间通讯的复杂性，并可视化复杂的相互作用网络。其他工具，如 iTALK、ICELLNET 和 SingleCellSignalR，为分析配体-受体 （L-R） 相互作用提供了进一步的功能和资源。 值得注意的是，Scriabin 能够在单细胞水平上检查细胞间通讯，揭示细胞相互作用的微妙网络。尽管如此，当前单细胞分析方法的一个显着缺点是它们无法完全捕获空间信息¹⁴。缺乏细胞空间信息增加了假阳性的可能性，导致将物理分离的细胞错误地归类为参与细胞间通讯的细胞¹⁵。因此，应将空间信息纳入 CCC 分析，以推进该领域并增强对这一复杂过程的理解¹⁶。

空间转录组学 （ST） 提供有关包含多个或部分细胞的细胞或斑点的宝贵空间信息 ^{17,18,19,20,21}。这些技术有助于测量具有不同细胞分辨率的二维 （2D） 或三维 （3D） 组织样本中的空间基因表达²²。ST 的加入显著提高了生物学和生物医学中空间 CCC 推理的准确性和可靠性。最近，出现了几种方法来破译空间背景下 CCC 的潜在机制。例如，CellPhoneDBv3（CPDB3） 限制了位于同一微环境中的细胞类型之间的相互作用，这由空间信息²³ 确定。stLearn 将配体和受体基因的共表达与细胞类型的空间多样性相关联²⁴。SVCA²⁵ 和 MISTy²⁶ 分别采用概率和机器学习模型来识别细胞之间空间相关的基因相互作用。NCEM²⁷ 使用函数来拟合细胞类型、空间环境和基因表达之间的关系。相比之下，乔托构建了空间近似图来识别通过膜结合受体结合的 L-R 对之间的相互作用²⁸。此外，SpaOTsc 在 scRNA-seq 和 ST 数据之间执行结构化最佳运输映射，为细胞分配空间位置，并使用细胞间距离作为运输成本来推断介导空间约束的配体-受体信号网络²⁹。 虽然这种方法量化了细胞间相互作用的可能性，但它对基于图像的空间表达数据的特异性和对预定义途径的依赖在一定程度上限制了它的多功能性和适用性。COMMOT³⁰ 是 SpaOTsc 最佳运输框架的扩展，通过对 ST 数据应用最佳运输分析工具来推断通信方向，同时考虑复杂的配体-受体相互作用和有效细胞间通信距离施加的限制。此外，NICHES³¹ 是该工具箱的一个显着补充，它利用空间转录组信息来理解单细胞分辨率的 CCC。事实证明，该工具对于更深入地了解组织内固有的复杂相互作用和组织模式非常宝贵。这些方法为在空间背景下直接分析 CCC 带来了巨大的希望。尽管如此，它们遇到了 ST 数据的基因通量和空间分辨率带来的限制。此外，这些方法中的大多数主要集中在识别配对细胞类型之间的 CCC，而忽略了配对单个细胞之间的 CCC 分析。能够同时克服 ST 数据局限性并以单细胞分辨率推断 CCC 的方法仍然很少，从而限制了我们对各种细胞在生物过程中表现出的协调活动的理解。

在这里，我们开发了 DeepTalk，这是一种创新方法，它结合了细胞特异性基因表达数据和细胞的空间亲和力，以单细胞分辨率预测 CCC。DeepTalk 采用图注意网络 (GAT) ³²以及基于子图的 GAT 来揭示健康和患病组织空间背景下 CCC 背后的复杂机制。通过将 ST 数据与来自相同区域的 scRNA-seq 数据相结合，这有效地克服了 ST 数据基因吞吐量受限和空间分辨率不足带来的限制。使用各种公开可用的数据集进行的广泛评估验证了 DeepTalk 在识别空间 CCC 方面的卓越性能和稳健性。我们的结果表明，DeepTalk 具有巨大潜力，可以在不同条件下发现有意义的 CCC 模式，并为组织内的空间细胞间动力学提供有价值的见解。

DeepTalk 工作流程概述

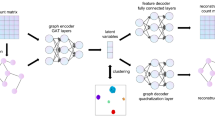
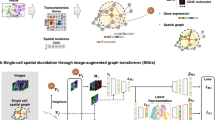
分析 scRNA-seq 和 ST 数据的两个关键任务是确定细胞类型和 CCC，因为这些任务可以深入了解细粒度的组织组织和细胞水平的通信。所提出的深度学习方法 DeepTalk 由两个主要部分组成：（1）DeepTalk-Integration（DT-Integration），它整合 sc/snRNA-seq 和 ST 数据以识别单细胞 ST 数据中的细胞类型并对非单细胞 ST 数据执行反卷积，以及 (2) DeepTalk-CCC (DT-CCC)，它以单细胞分辨率预测处理后的 ST 数据的空间分辨细胞间通信（图 1a）。最初，GAT 被用于“解码”单细胞或基于点的 ST 数据矩阵。这个解码过程涉及利用自注意力机制来关注 scRNA-seq 或 ST 数据中的关系，并利用交叉注意力机制来捕捉 scRNA-seq 数据和 ST 数据之间的联系。通过此解码步骤，生成一个权重矩阵，表示每个细胞或点的细胞类型的最佳比例（图 1b）。细胞被标记为单细胞 ST 数据中权重最大的细胞类型，而不同细胞类型和不同权重的细胞则用于基于点的 ST 数据作为参考，将 scRNA-seq 数据中的细胞投影到空间点上。通过迭代过程，进一步细化细胞的最佳组合，以重建基于点的单细胞 ST 数据（图 1c）。

DeepTalk 将单细胞 RNA 测序（scRNA-seq）数据和空间转录组学（ST）数据作为输入。b 数据中的细胞关系，并利用交叉注意力机制探索 scRNA-seq 和 ST 数据之间的联系，DeepTalk-Integration 生成一个权重矩阵，该矩阵表示每个细胞或点的最佳细胞类型比例。c DeepTalk-Integration 的整合结果。它主要包含对空间测量基因的低质量数据的校正、细胞类型定位和单细胞反卷积。d DeepTalk- 使用基于子图的注意力图神经网络预测细胞间通信。e DeepTalk CCC 为单细胞水平的空间分辨细胞间通信提供可视化输出。 ( )中的组织组件由 BioRender.com 制作，根据 Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International 许可发布。
a DeepTalk 将单细胞 RNA 测序 （scRNA-seq） 数据和空间转录组学 （ST） 数据作为输入。b DeepTalk-Integration 使用注意力图神经网络集成 scRNA-seq 和 ST 数据。通过采用自我注意机制来捕获 scRNA-seq 或 ST 数据中的细胞关系，并利用交叉注意力机制来探索 scRNA-seq 和 ST 数据之间的联系，DeepTalk-Integration 生成了一个权重矩阵，代表每个细胞或斑点的最佳细胞类型比例。c DeepTalk-Integration 的集成结果。它主要包含空间测量基因的低质量数据的校正、细胞类型定位和单细胞反卷积。d DeepTalk-CCC 使用基于子图的注意力图神经网络预测细胞间通信。e DeepTalk-CCC 为单细胞水平的空间分辨细胞间通讯提供可视化输出。（a） 中的组织组件是使用 BioRender.com 创建的，根据 Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International 许可证发布。

全尺寸图像

随后，DT-CCC 通过创建包含距离信息和细胞表达数据的细胞图来建立细胞之间的连接，从而以单细胞分辨率推断 CCC。这种构造考虑了细胞的位置和相似性，反映了它们的空间排列。为每个细胞生成单独的子图，通过子图编码器对其局部特征进行编码。为了捕捉细胞在其空间环境中的局部特征，DT-CCC 使用基于子图的 GAT ³³，这使其能够根据来自相邻细胞的数据评估每个细胞的特征（图 1d）。该模型通过理解局部细胞间关系来掌握细胞位置和相互作用。它整合所有细胞的不同特征，并使用基于注意力的图神经网络破译它们之间的潜在联系。这种方法能够推断 CCC 并在空间层面理解细胞相互作用。此外，为了增强模型的泛化能力，采用了预训练和微调策略³⁴。通过在大规模数据集上进行预训练，该模型学习了细胞间通讯和空间关系的一般模式。随后对特定数据集进行微调可提高模型预测 CCC 的准确性。这种训练方法有助于提高模型推断细胞间通讯的稳健性和准确性。此外，DT-CCC 还提供可视化功能，可以直观地展示细胞类型的组成和空间细胞间通讯（图 1e）。与其他最先进的方法相比，DT-CCC 在应用于基于点的 ST 和单细胞 ST 数据时表现出色。

DeepTalk-Integration 与最先进的集成方法的性能比较

ST 和 scRNA-seq 数据的整合对于准确阐明空间背景下的复杂 CCC 至关重要。为了增强对 CCC 的理解，我们利用空间转录本分布模型对未检测到的转录本的预测能力，并对组织样本进行复杂的细胞类型反卷积分析。为了评估我们方法的整合效率，我们提出了 DT-Integration 并将其与八种尖端技术进行比较，利用由 Li 等人整理的多样化数据集³⁵，该数据集包含 45 组配对的 ST 和 scRNA-seq 数据集。ST 数据集使用各种技术，包括 osmFISH ³⁶、seqFISH ¹⁹、MERFISH ³⁷、STARmap ³⁸、ISS ³⁹、BaristaSeq ⁴⁰、ST ⁴¹、10X Visium ⁴²、Slide-seq ¹⁸和 HDST ⁴³。这些数据集可分为基于图像和基于序列 (seq-based) 的方法⁴⁴。基于图像的 ST 方法（例如原位杂交和荧光显微镜）可以高分辨率和高精度地检测转录本的空间分布；但是，它们可能在检测到的转录本数量方面受到限制。基于 Seq 的 ST 方法使用空间定义的点捕获整个转录组规模的 RNA 表达，并表现出高技术覆盖率但低空间分辨率。此外，Drop-seq ⁴⁵、Smart-seq ⁴⁶和 10X Chromium ⁴⁷等技术用于生成 scRNA-seq 数据集。

首先，我们对 DT-Integration 以及其他八种集成方法的性能进行了严格的评估：Tangram ⁴⁸、gimVI ⁴⁹、SpaGE ⁵⁰、Seurat ⁵¹、SpaOTsc ²⁹、novoSpaRc ⁵²、LIGER ⁵³和 stPlus ⁵⁴。我们的评估重点是预测 ST 数据集内未检测到的 RNA 转录本的空间分布。为了保证严格和可重复的测试，我们对 45 个配对数据集采用了十倍交叉验证⁵⁵技术。为了系统地评估这八种集成方法在预测未检测到的转录本的空间分布方面的能力，我们使用了多个指标：皮尔逊相关系数 (PCC) ⁵⁶、结构相似性指数 (SSIM) ⁵⁷、均方根误差 (RMSE) ⁵⁸、Jensen-Shannon 散度 (JSD) ⁵⁹和准确度得分 (AS) ³⁵。这些指标对 45 组配对数据集的预测准确性、结构相似性、误差幅度、发散度和总体性能提供了稳健的评估（图 2a，补充图 1和2）。因此，DT-Integration 被证明是最好的方法，在基于图像和基于序列的数据集中都超越了其他方法。

a Boxplots showcasing the Accuracy Score of nine different integration methods across all 45 paired datasets, encompassing 28 sequence-based and 17 image-based datasets. The boxplots display data distribution where the box spans from the first to the third quartile, marking the median with a distinct line. The whiskers reach out to the maximum range within 1.5 times the interquartile range, and individual outliers are denoted by separate dots. b A STARmap slide from the STARmap dataset (mouse visual cortex), annotated with various cell types. Each grid portrays a simulated spot encompassing multiple cells. c Illustration of the proportion of Layer 4 (L4) excitatory neurons within simulated spots from the STARmap dataset, alongside predictions from eight integration methods. d Boxplots presenting the PCC, SSIM, RMSE, and JSD for eight integration methods, specifically analyzed for the STARmap dataset. The boxplots display data distribution where the box spans from the first to the third quartile, marking the median with a distinct line. The whiskers reach out to the maximum range within 1.5 times the interquartile range; n = 189 predicted spots. e A seqFISH+ slide from the seqFISH+ dataset (mouse cortex), annotated with cell types. Analogous to the STARmap slide, each grid symbolizes a simulated spot with multiple cells. f Depiction of the proportion of L4 excitatory neurons in simulated spots from the seqFISH+ dataset, accompanied by predictions from eight integration techniques. g Boxplots exhibiting the metrics of PCC, SSIM, RMSE, and JSD for the eight integration methods tested on the seqFISH+ dataset. The boxplots display data distribution where the box spans from the first to the third quartile, marking the median with a distinct line. The whiskers reach out to the maximum range within 1.5 times the interquartile range; n = 72 predicted spots. Source data are provided as a Source Data file.

Full size image

Second, we evaluate the performances of DT-Integration and seven other integration methods (Tangram, Cell2location⁶⁰, SpatialDWLS⁶¹, RCTD⁶², Stereoscope⁶³, DestVI⁶⁴, and SPOTlight⁶⁵) for cell-type deconvolution. For the purpose of comparing their performances, we utilize the STARmap and seqFISH+ datasets as our baselines. Additionally, we simulate a “grid” that represents low spatial resolution datasets, following a precedent established in previous research³⁵. In these simulated low-resolution datasets, each “spot” within the grid contains a varying number of cells, ranging from 1 to 18, much like the ST datasets that are generated using techniques such as 10X Visium or ST methods. The STARmap dataset captures 1549 cells corresponding to 15 cell types³⁸ (Fig. 2b). After grid transformation, the simulated dataset comprises 189 spots, each containing 1–18 cells. In identifying the positions of L4 excitatory neurons, DT-Integration demonstrated high accuracy and consistency, achieving a Pearson correlation coefficient (PCC) of 0.88, the highest among all methods. RCTD and Stereoscope closely followed with a PCC of 0.87 (Fig. 2c). For a broader analysis, we also plotted the positions of Layer 2/3(L2/3) and L5 excitatory neurons (Supplementary Fig. 3).

Additionally, we used metrics like PCC, SSIM, RMSE, and JSD to assess the accuracy of these eight integration methods in predicting cell-type composition within the simulated grid dataset (Fig. 2d). Our evaluations consistently showed that DT-Integration surpassed the other seven methods. We extended this analysis to the seqFISH+ dataset, which included 72 simulated spots¹⁹ (Fig. 2e). Using the true positional values of L4 excitatory neurons, we found that DT-Integration achieved the highest PCC value of 0.69 (Fig. 2f). We also mapped the positions of L5/6 excitatory neurons for clarity (Supplementary Fig. 4). Across all cell types, DT-Integration excelled in terms of PCC, SSIM, RMSE, and JSD (Fig. 2g). To enhance the robustness of our evaluation, we incorporated 32 simulated datasets compiled by Lin et al.³⁵ Once again, DT-Integration proved its superiority over the other methods, consistently outperforming them across multiple metrics (Supplementary Fig. 5).

Identification of spatially resolved CCCs in mouse visual cortex using the MERFISH dataset

DeepTalk was employed to analyze the MERFISH dataset, encompassing measurement data for 268 genes across 2399 cells originating from the VISp (visual cortex) region of the mouse²⁰. To train the DeepTalk- Integration model, a total of 254 genes common to both MERFISH and snRNA-seq datasets were aligned with 11,759 SMART-Seq2 snRNA-seq records from the VISp region⁶⁶. This alignment served to reveal the spatial distribution of various cell types. The derived probability mappings were then fused with cell-type annotations sourced from the snRNA-seq data, resulting in spatial probability distributions for each distinct cell type (Fig. 3a). It’s worth noting that glutamatergic cells demonstrated unique patterns across different cortical layers, while the majority of non-neuronal cells and GABAergic neurons showcased a granular distribution, aligning with established research findings⁴⁸. Furthermore, a deterministic mapping was conducted by assigning the most probable cell types to their respective spatial locations, providing a visualization of the cell type distributions (Fig. 3b).

a snRNA-seq 数据在 MERFISH 数据上的概率映射。为三个主要类别中的每个细胞子集分配一个似然分数，表明它们的潜在细胞类型。b细胞类型的确定性映射。在 MERFISH 幻灯片上显示分割的细胞，根据使用 DeepTalk-Integration 映射的最可能的 snRNA-seq 配置文件进行颜色编码。c使用 MERFISH 数据集对 DeepTalk-CCC (DT-CCC) 进行ROC曲线评估。该曲线说明了 DT-CCC 在真阳性率与假阳性率方面的表现。d CCC 工具评估的DES排名。对各种细胞间通讯工具的比较分析，根据它们在评估过程中的表现进行排名。箱线图显示数据分布，其中箱线跨越从第一四分位数到第三四分位数，用一条明显的线标记中位数。须线延伸到四分位距 1.5 倍以内的最大范围，单个异常值用单独的点表示；n  = 5 次重复独立测试。e相邻和远处细胞类型之间的通讯分数比较。突出显示第 4 层 (L4) 细胞与其他细胞类型（包括 L2/3 端脑内神经元 (IT)、L5 IT、L5 锥体束神经元 (PT) 和 L6 PT）之间基于空间接近度的通讯分数差异。箱线图显示数据分布，其中箱子跨越第一四分位数到第三四分位数，用一条明显的线标记中位数。晶须延伸到四分位距 1.5 倍以内的最大范围，各个异常值用单独的点表示；N：预测的 LR（配体-受体）对的数量。f通过低维嵌入可视化 CCC。图中的每个点代表一个 CCC 事件，其中细胞充当受体细胞。g在单细胞水平上比较空间相邻和远处细胞之间的 CCC 分数。该图在单细胞水平上比较了空间相邻细胞和远距离细胞之间的通信分数，揭示了基于接近度的通信强度差异。箱线图显示数据分布，其中箱线从第一四分位数跨越到第三四分位数，用一条明显的线标记中位数。晶须延伸到四分位数间距的 1.5 倍内的最大范围，单个异常值用单独的点表示；n  = 169 个 L4 细胞。h通过低维嵌入查看局部微环境。该图中的每个点代表一组 CCC 事件，其中感兴趣的细胞作为接收器。i由 Apoe - Grm5 对介导的预测 CCC。它包括谷氨酸能细胞之间由 Apoe - Grm5 对介导的 CCC 得分（左）以及从 L2/3 IT 细胞到 L4 细胞的预测 CCC（右）。源数据以源数据文件的形式提供。

全尺寸图像

随后，DT-CCC 用于预测该 MERFISH 数据集由 L-R 对介导的 CCC。为了评估 DT-CCC 的预测能力，使用 ROC 曲线来表示在 L-R 对介导下 CCC 最多的前 5 个 L-R 对的预测性能（图 D）。基于 DT-CCC 预测结果，由 L-R 对介导的 CCC 的曲线下面积 （AUC） 值在 0.84 和 0.95 之间，表明所提出的方法在评估 L-R 对的影响方面具有较高的准确性和可靠性。此外，将 DT-CCC 与其他预测方法进行了比较，包括统计方法 （例如，CellCall⁶⁷、CellChat、CellPhoneDB、ICELLNET、iTALK 和 SingleCellSignalR）、基于网络的方法 （例如，Connectome 和 NicheNet） 和基于 ST 的方法 （例如，Giotto、CellChatv2⁶⁸、CPDB3、COMMOT 和 stLearn）。距离富集评分 （DES） 作为评估预期空间模式与观察到的 CCC⁶⁹ 之间一致性的基准，评估细胞间空间趋势的一致性。DT-CCC 在 CCC 预测方面被证明是优越的，实现了 0.45 的显着 DES，明显优于其他方法（图 D）。通过整合空间数据，我们改进了 DT-CCC 的预测准确性，基于以下假设：CCCs 在相邻细胞类型中比远处细胞类型更明显。为了展示不同邻近细胞之间 CCC 的范围，我们精心挑选了五种细胞类型——L2/3 端脑内神经元 （IT）、L4、L5 IT、L5 锥体束神经元 （PT） 和 L6 PT——以其在谷氨酸能细胞中的聚集趋势而闻名（图 D）。然后，我们计算了这些细胞之间的空间距离（补充图 D）。6）. 我们的结果表明，L2/3 IT 单元靠近 L4，而 L6 PT 离 L4 最远。以 L4 为基线，我们计算了 L4 和其他细胞组之间的 CCC 概率。与其他 13 种方法（图 .3e 和补充图7），DT-CCC 在区分紧密和远距离相互作用的细胞类型方面明显表现出色。

为了进一步测试 DT-CCC 在单细胞分辨率下的预测能力，我们将其与 NICHES 和 Scrabin 这两种推断细胞间通讯的领先技术进行了基准测试。我们选择了五种特定的细胞类型——L2/3 IT、L4、L5 IT、L5 PT 和 L6 PT——进行分析。通过使用低维嵌入，我们可视化了它们的 CCC 模式，可视化中的每个点都表示一个 CCC 事件，特别关注接收单元（图 D）。这种可视化技术强调了 DT-CCC 在识别各种细胞类型之间细微的通信模式方面的熟练程度。此外，我们比较了单细胞分辨率下的 CCC 强度。DT-CCC 和 NICHES 都同意，与远处细胞相比，空间上邻近的细胞表现出更明显的 CCC，这与之前的假设一致（图 D）。3g）。然而，没有纳入空间数据的 Scrabin 往往会忽略这些空间关系，导致 CCC 模式评估的准确性较低（图 D）。总体而言，DT-CCC 在区分 CCC 模式方面表现出色，强调了空间位置在塑造细胞微环境中的重要性。

我们还选择性地分析了不同空间距离的谷氨酸能细胞，并表明CCC由LR对介导（图 3i，补充图 8和9）。载脂蛋白（Apoe）E ^{70是一种参与脂质代谢和运输的关键蛋白质，它可能通过与代谢型谷氨酸受体5（Grm5） 71}的结合来调节小鼠视觉皮层的神经功能。这种相互作用可能调节突触可塑性和神经连接的稳定性，这对于视觉信号传递和信息处理至关重要。Apoe的存在可能改变Grm5的激活模式，从而影响谷氨酸信号的传递和神经元活动。通过与Grm5结合，Apoe可以通过调节谷氨酸能神经递质的释放和浓度来影响小鼠视觉皮层神经元之间的突触传递，并调节视觉信息处理和感知。此外，Apoe的结合还能调节神经炎症反应和细胞凋亡，对小鼠视觉皮层损伤和疾病发展起到保护作用。Apoe与Grm5的相互作用通过调节谷氨酸信号传递、突触可塑性和神经连接稳定性显著影响小鼠视觉皮层，从而影响视觉信息的正常传递和神经功能。热图可视化显示相邻细胞类型之间发生CCC的频率更高，揭示了细胞距离在促进CCC中的重要性。除了展示与距离相关的CCC模式之外，我们还研究了Apoe-Grm5介导的L2/3和L4细胞之间前50种通讯，旨在从单细胞分辨率上更深入地了解CCC。

使用 10X Visium 数据在单细胞水平上描绘成年小鼠大脑中的空间分辨 CCC

DeepTalk 模型用于分析从成年小鼠大脑获得的低分辨率 ST（10X Visium）数据中的细胞间通讯^{72 。对皮质簇进行了研究和分析}，该数据集提供了对信号传输和细胞间相互作用的洞察。最初，标准 Scanpy 函数用于预处理 Visium 数据^48、73（如方法中所示），识别出 324 个点和 16,562 个基因（图 4a ）。为了克服低分辨率带来的限制，使用^Squidpy函数将细胞分配到每个体素，确保每个细胞的分割切片数量相等。这种确定性方法能够精确映射每个体素内的每个细胞，从而以单细胞分辨率预测细胞定位（图 4b）。这些预测有助于将细胞类型与其空间位置相关联，从而揭示细胞间通讯的重要模式和机制。

条表示映射谷氨酸能细胞的概率。b每个点的细胞数（左）和 10X Visium 载玻片，其中分割的细胞由 DeepTalk-Integration 映射到该位置的最可能的 snRNA-seq 谱的细胞类型注释着色（右）。c从第 5 层端脑内神经元 (L5 IT) 细胞到其他细胞类型的预测细胞间通讯 (CCC) 的分数。d使用 Visium 数据集对 DeepTalk-CCC (DT-CCC) 进行 ROC 曲线评估。该曲线说明了 DT-CCC 在真阳性率与假阳性率方面的表现。e CCC 工具评估的DES排名。对各种 CCC 工具进行比较分析，根据其在评估过程中的表现进行排名。箱线图显示数据分布，其中箱子从第一四分位数跨越到第三四分位数，用一条明显的线标记中位数。晶须延伸到四分位距的 1.5 倍以内的最大范围，各个异常值用单独的点表示；n  = 5 次重复独立检验。f相邻和远处细胞类型之间的通讯分数比较。突出显示 L4 细胞与其他细胞类型（包括 L2/3 IT、L5 IT、L6 IT 和 L6 皮质丘脑神经元 (CT)）之间基于空间接近度的通讯分数差异。箱线图显示数据分布，其中箱子从第一四分位数跨越到第三四分位数，用一条明显的线标记中位数。晶须延伸到四分位距的 1.5 倍以内的最大范围，各个异常值用单独的点表示；N：预测的 LR（配体-受体）对的数量。g通过低维嵌入对 CCC 进行可视化。图中的每个点代表一个CCC 事件，其中细胞充当受体细胞。h在单细胞水平上比较空间相邻和远处细胞之间的 CCC 分数。该图在单细胞水平上比较空间相邻细胞和远处细胞之间的通信分数，揭示了基于接近度的通信强度差异。箱线图显示数据分布，其中箱子从第一四分位数跨越到第三四分位数，用一条明显的线标记中位数。晶须延伸到四分位距 1.5 倍的最大范围，单个异常值用单独的点表示；n  = 600 个 L4 细胞。i通过低维嵌入查看局部微环境。该图中的每个点代表一组 CCC 事件，其中感兴趣的细胞充当接收器。j
scRNA-seq 数据到 10X Visium 数据的概率映射。颜色条表示绘制谷氨酸能细胞的概率。b 每个斑点的细胞数（左）和 10X Visium 玻片，其中分割的细胞由 DeepTalk-Integration 映射到该位置的最可能的 snRNA-seq 谱的细胞类型注释着色（右）。c 从第 5 层端脑内神经元 （L5 IT） 细胞到其他细胞类型的预测细胞间通讯 （CCC） 的分数。d 使用 10X Visium 数据集对 DeepTalk-CCC （DT-CCC） 的 ROC 曲线评估。该曲线说明了 DT-CCC 在真阳性率与假阳性率方面的性能。e CCC 工具评估的 DES 排名。对各种 CCC 工具的比较分析，根据它们在评估过程中的表现进行排名。箱线图显示箱形从第一四分位数跨越到第三四分位数的数据分布，并用一条明显的线标记中位数。须线达到四分位间距 1.5 倍以内的最大范围，单个异常值用单独的点表示;n = 5 次重复独立测试。f 相邻和远距离细胞类型之间的通信分数比较。突出显示 L4 细胞与其他细胞类型（包括 L2/3 IT、L5 IT、L6 IT 和 L6 皮质丘脑神经元 （CT））之间基于空间邻近性的通信评分差异。箱线图显示箱形从第一四分位数跨越到第三四分位数的数据分布，并用一条明显的线标记中位数。须线达到四分位间距 1.5 倍以内的最大范围，单个异常值用单独的点表示;N：预测的 L-R（配体-受体）对的数量。 g 通过低维嵌入实现 CCC 的可视化。图中的每个点都代表一个 CCC 事件，该细胞用作受体细胞。h 单细胞水平空间相邻和遥远细胞之间的 CCC 评分比较。该图在单小区级别比较了空间相邻小区和远距离小区之间的通信分数，揭示了基于邻近度的通信强度的差异。箱线图显示箱形从第一四分位数跨越到第三四分位数的数据分布，并用一条明显的线标记中位数。须线达到四分位间距 1.5 倍以内的最大范围，单个异常值用单独的点表示;n = 600 个 L4 细胞。i 通过低维嵌入观察的局部微环境。此图中的每个点都表示 CCC 事件的集合，其中感兴趣的 cell 充当接收器。j由 Psen1 - Pparg 对介导的预测 CCC。谷氨酸能细胞中由 Psen1 - Pparg 对介导的 CCC 得分（左）和从 L2/3 IT 细胞到 L4 细胞的预测 CCC（右）。源数据以源数据文件的形式提供。

全尺寸图像

为了进一步提高预测精度，我们结合 10X Visium 和 scRNA-seq 数据训练了一个模型，其中包含 1291 个基因⁷⁴。随后，将该模型应用于从成年小鼠皮质区域获得的 scRNA-seq 数据，该数据包含 21,697 个细胞⁶⁶。通过将概率映射结果与从 snRNA-seq 数据获得的细胞类型注释合并，获得空间环境中不同细胞类型的概率分布（图 4a）。基于确定性映射结果，将最可能的细胞类型分配给每个空间位置，以直观地表示细胞类型分布（图 4b）。这种综合方法为细胞定位、细胞类型分类和细胞间通讯网络的整体结构提供了宝贵的见解。

为了研究细胞间通讯机制的细节，我们采用 DT-CCC 模型来预测由各种 LR 对介导的 CCC。由于谷氨酸能细胞之间的空间距离不同，本研究将谷氨酸能细胞作为目标细胞。根据 CCC 与其他谷氨酸能细胞的强度，我们主要探讨了 L5 IT 细胞与前 50 个 LR 对之间的相互作用。这些相互作用对的热图可视化显示，靠近 L5 IT 细胞的细胞表现出更强的通讯（图 4c）。这表明 L5 IT 细胞和谷氨酸能细胞在特定空间位置之间存在密切的联系和通讯。为了评估 DT-CCC 模型的预测能力，我们为参与 CCC 的前 10 个 LR 对生成了 ROC 曲线（图 4d）。根据 DT-CCC 预测，LR 配对介导的 CCC 的最高 AUC 值为 0.96。利用 DES 作为性能指标，我们将 DT-CCC 的功效与其他预测方法进行了比较（图 4e）。

为了了解距离不同细胞之间复杂的通讯模式，我们专门选择了五个谷氨酸能细胞簇 - L2/3 IT、L4、L5 IT、L6 IT 和 L6 皮质丘脑神经元（CT），它们以聚集行为而著称（图 4a）。我们确定了这些细胞之间的空间关系（补充图 11），发现 L2/3 IT 细胞与 L4 紧密相邻，而 L6 CT 细胞距离 L4 最远。以 L4 为参考，我们计算了 L4 与其他细胞类型之间的通讯概率。在与 13 种替代方法的比较分析中（图 4f和补充图 12），DT-CCC 证明了其在区分紧密和远距离通讯的细胞类型方面的优势。

在评估 DT-CCC 在单细胞水平上预测 CCC 的精度时，我们将其与 NICHES 和 Scrabin 进行了比较。我们将重点缩小到五种细胞类型：L2/3 IT、L4、L5 IT、L6 IT 和 L6 CT。利用低维嵌入，我们将每个 CCC 事件表示为一个点，强调接收细胞（图 4g）。这种方法强调了 DT-CCC 区分不同细胞间通讯模式的能力。此外，我们在单细胞水平上评估了 CCC 强度，发现 DT-CCC 和 NICHES 都准确地预测了空间上邻近细胞中更强的 CCC（图 4h）。然而，Scrabin 在这次评估中有所欠缺。为了更深入地了解局部细胞环境，我们使用低维嵌入可视化邻近细胞，每个点代表以特定接收细胞为中心的一组 CCC 事件（图 4i）。 DT-CCC 再次在辨别不同的 CCC 模式方面表现出色。

还展示了由基因对 Psen1-Pparg 介导的谷氨酸能细胞之间的 CCC 结果（图 4j，补充图 13和14）。Psen1（早老素 1）与阿尔茨海默病密切相关，在细胞内信号转导和膜蛋白转运中发挥关键作用⁷⁵。相反，Pparg（过氧化物酶体增殖激活受体γ）属于核受体超家族，作为转录因子发挥作用，监督脂肪细胞分化、葡萄糖代谢和炎症反应等多种生物过程⁷⁶。谷氨酸促进的细胞间通讯本质上依赖于神经递质谷氨酸的细致释放和接收，这一过程受到一系列因素的细致调节，包括细胞内信号级联和调节因子的转录活性。热图可视化有效地展示了这种复杂的关系。此外，我们的分析还确定了观察到 Psen1-Pparg 介导的前 50 对 L2/3 和 L4 细胞。这些结果揭示了细胞间连接的模式和特定条件下的通信强度。深入探索这些 CCC 可以深入了解它们在细胞和组织功能中的重要性，增强我们对神经网络内复杂相互作用的理解。通过阐明这些连接，我们可以更好地理解神经通信的复杂性，并有可能开发出更有针对性的神经系统疾病治疗方法。

综上所述，我们尝试将DT-CCC模型应用于低分辨率ST数据中的细胞间通讯分析，并取得了一些有希望的初步结果。通过该模型对细胞类型定位、概率映射和CCC的预测，我们揭示了细胞间通讯网络的复杂结构和组织。

使用 ST 数据集在人胰腺导管腺癌中以单细胞分辨率进行 CCC 的空间表示

DeepTalk 算法用于分析从人类胰腺导管腺癌 (PDAC) 数据集⁴¹获取的 ST 数据，该数据集使用 ST 技术生成，涵盖各种组织区域，包括癌症、胰腺、导管和基质区域 (图 5a ) ⁴¹。为确保数据的准确性和可靠性，专业组织学专家使用 H&E 染色对这些区域进行了注释。首先，我们重建了单细胞 ST 数据，并对其进行整合和分析，以研究各种 PDAC 细胞类型的分布和基因表达特征 (图 5a )。为了解决任何不确定性，使用来自同一个体的匹配的 scRNA-seq 数据 (PDAC-A) 进行反卷积 (图 5b )。DT-CCC 将不同类型的细胞分配给它们特定的组织区域，从而有助于探索 PDAC 内复杂的细胞组成和空间关系。

a PDAC 数据的注释空间区域（左）与 scRNA-seq 数据到 ST 数据的概率映射（右）并列。b ST 幻灯片展示了分割细胞，根据 DeepTalk-Integration 映射的最可能的 scRNA-seq 图谱着色。c 分数表示癌症克隆 A、癌症克隆 B 和其他细胞类型之间的预测细胞间通讯 （CCC）。d 使用 ST 数据集评估 DeepTalk-CCC （DT-CCC） 的 ROC 曲线。该曲线说明了 DT-CCC 在真阳性率与假阳性率方面的性能。e CCC 工具评估的 DES 排名。对各种 CCC 工具的比较评估，根据它们的评估性能进行排名。箱线图显示箱形从第一四分位数跨越到第三四分位数的数据分布，并用一条明显的线标记中位数。须线达到四分位间距 1.5 倍以内的最大范围，单个异常值用单独的点表示;n = 5 次重复独立测试。f 相邻和远距离细胞类型之间的通信分数比较。突出癌症克隆 A （CCA） 细胞与其他细胞类型（包括癌症克隆 B （CCB）、导管末端 （DT）、导管抗原呈递 （DAP） 和导管中心腺粒 （DC））之间基于空间邻近的通信评分差异。箱线图显示箱形从第一四分位数跨越到第三四分位数的数据分布，并用一条明显的线标记中位数。须线达到四分位间距 1.5 倍以内的最大范围，单个异常值用单独的点表示;N：预测的 L-R（配体-受体）对的数量。g 细胞间通讯的可视化。 将 CCC 事件表示为低维嵌入中的点，并指示接收单元。h 通信分数的单细胞水平比较。比较相邻和远距离单元格之间的通信分数，揭示基于邻近度的强度差异。i 局部微环境可视化。表示 CCC 事件的集合，其中感兴趣的单元在低维嵌入中充当接收器。箱线图显示箱形从第一四分位数跨越到第三四分位数的数据分布，并用一条明显的线标记中位数。须线达到四分位间距 1.5 倍以内的最大范围，单个异常值用单独的点表示;n = 127 个癌症克隆 A 细胞。j 预测由 EFNA5-EPHA2 对介导的 CCC。显示导管细胞和癌细胞之间由 EFNA5-EPHA2 对介导的 CCC 的分数，并预测从癌症克隆 A 细胞到导管末端细胞的 CCC。源数据作为 源数据 文件提供。

全尺寸图像

DT-CCC 用于预测 PDAC 数据集中细胞之间的通讯。生成热图以直观地表示癌症克隆 A、癌症克隆 B 和邻近细胞之间的通信强度，由特定的 L-R 对介导（图 D）。值得注意的是，结果表明预测的相互作用强度与细胞类型之间的空间距离之间存在正相关，这表明距离较近的细胞更有可能进行交流，从而更深入地了解 PDAC 组织中细胞间信息的传递和相互作用机制。

为了评估 DT-CCC 的预测准确性，我们生成了前 10 个 L-R 对的 ROC 曲线，重点是 CCC 准确性（图 D）。我们的 DT-CCC 预测表明，由 LR 配对介导的 CCC 的 AUC 值在 0.82 和 0.93 之间。此外，根据 DES 指标，与其他方法相比，DT-CCC 表现出卓越的 CCC 预测准确性（图 D）。5e）。

为了深入了解各种细胞类型之间根据距离之间的复杂相互作用，我们精心挑选了五个细胞群进行详细分析：癌症克隆 A、癌症克隆 B、导管末端、导管抗原呈递和导管中心腺细胞（图 D）。通过查阅补充图 1 中映射的细胞位置。16 中，我们精确计算了这些细胞之间的空间距离。我们的调查揭示了一个值得注意的模式：癌症克隆 B 细胞与癌症克隆 A 细胞非常接近，而导管中心细胞距离最远。以癌症克隆 A 细胞为基准，我们探讨了与其他细胞群相互作用的可能性。当将 DT-CCC 的预测通信强度与其他 13 种方法进行比较时（图 D）。5f 和补充图17），很明显，DT-CCC 在区分近距离和远距离通信的细胞方面大放异彩。

为了严格评估 DT-CCC 在单细胞水平上 CCC 预测的准确性，我们将其与 NICHES 和 Scrabin 进行了比较。针对我们的五种关键细胞类型，我们采用低维嵌入来可视化它们的 CCC 模式。在此可视化中，每个 CCC 事件都表示为一个点，重点是接收单元（图 D）。5g）。这强调了 DT-CCC 区分各种细胞间通讯模式的非凡能力，尽管细胞亚型之间的相似通讯模式带来了挑战。此外，我们分析了单细胞水平的 CCC 强度，发现 DT-CCC 和 NICHES 都表明空间相邻细胞之间的 CCC 更强烈（图 D）。5h）。虽然 NICHES 反映了空间信息，但 Scrabin 在这方面存在不足。为了更深入地研究，我们使用低维嵌入来可视化特定接收细胞周围的细胞，每个点代表以该细胞为中心的一组 CCC 事件（图 D）。尽管在区分局部微环境方面存在挑战，但 DT-CCC 在反映细胞的局部通讯环境方面优于其他方法。

^{配体 EFNA5 77}与受体 EPHA2 ⁷⁸之间的相互作用在人体各种生理和病理过程中起着至关重要的作用，特别是在调节细胞间通讯方面。EPHA2 是一种受体酪氨酸激酶，它与各种 Ephrin-A 配体（包括 EFNA5）进行双向信号传导，从而影响细胞过程，例如迁移、粘附、增殖和分化。在 PDAC 的背景下，这些细胞行为尤其重要，因为它们与肿瘤的生长、侵袭和转移密切相关。作为 EPHA2 的配体，EFNA5 与受体相互作用以诱导双向信号传导，调节神经元、血管系统和上皮细胞的粘附、组织和发育。在 PDAC 中，这种相互作用可以影响肿瘤细胞的粘附性和迁移能力，从而改变肿瘤的生长模式和转移潜能。这里展示的热图说明了 EFNA5-EPHA2 在 PDAC 组织中介导的 CCC 潜力。这些热图为更深入地研究相关信号通路和细胞功能提供了宝贵的见解（图 5j）。此外，我们以单细胞分辨率展示了由 EFNA5-EPHA2 介导的从癌症克隆 A 细胞到导管末端细胞的前 50 个 CCC。这些发现揭示了不同条件下特定细胞之间通讯的各种相互作用模式和强度（补充图 18和19）。这些详细信息提供了对动态 CCC 及其在细胞和组织水平的功能调节中的关键作用的更全面的理解。

DeepTalk 是一种强大的方法，旨在阐明 CCC 的机制和功能。它利用基于注意机制的 GNN 来准确预测介导细胞间通讯的 L-R 对，并在多个尺度上可视化 CCC。验证实验证明了 DeepTalk 具有识别和可视化由显著丰富的细胞间 L-R 对介导的空间通信的卓越能力。为了证实 DeepTalk 的有效性和多功能性，我们使用了各种代表性实验数据集，例如从 MERFISH 获得的单细胞 ST 数据集和使用 ST 和 10x Visium 获得的基于点的 ST 数据集。这些数据集包括与各种技术平台和实验条件有关的 ST 信息，涵盖了错综复杂且多样的 CCC。它们证实了 DeepTalk 适用于不同类型的数据类型，进一步验证了其通用性和可靠性。

DeepTalk 是一种适用于单细胞和基于点的 ST 数据集的巧妙方法。这是通过合并 scRNA-seq 和 ST 数据集来实现的，从而提升了 CCC 分析。对于单细胞 ST 数据集，它采用相似性驱动的分类方法。它不依赖于表达模式，而是通过精确定位最相似和排名靠前的细胞簇来对这些数据集进行细致的分类和分析。其注意力机制驱动的 GNN 揭示了相关关系和细胞间相关模式，从而提高了分类准确性和可靠性。在处理基于点的 ST 数据集时，DeepTalk 引入了一种尖端的数据重建技术。通过仔细选择和映射最佳细胞组合，它在单细胞级别重新创建 ST 图，包含有关已知细胞类型的细节。这种策略揭示了细胞间连接和空间分布模式，有效地将基于点的 ST 数据转换为单细胞分辨率的 ST 数据。这不仅增强了数据的可解释性，而且提高了信息的准确性。 scRNA-seq 和 ST 数据集的整合拓宽了我们对 CCC 各个维度和层面的理解。scRNA-seq 数据提供了对细胞内基因表达的复杂见解，而 ST 数据揭示了细胞间的相互作用和相关性。通过融合这些数据类型，DeepTalk 呈现了一个整体和多方面的视角，促进了对 CCC 机制的更深入了解。

DeepTalk 探索了不同细胞类型之间的通信偏好，并确定了这些偏好在各种 ST 数据集中的趋势。DeepTalk 分析可用于在重建的单细胞分辨率下准确表征每种细胞类型的空间分布，从而提供有关不同细胞类型之间邻近关系的信息。利用基于子图的 GNN，DeepTalk 在多个层面上检查细胞相互作用，促进了一种多方面的分析方法，有助于构建细胞间通信网络并揭示复杂的互连模式。通过研究这些网络，可以更准确地确定不同细胞类型之间的通信模式和关系特征。此外，DeepTalk 促进了邻近 LRI 的统计分析和可视化，通过提供细胞间动态通信网络的可视化表示，扩展了对 CCC 机制和模式的理解。此外，LRI 分析可以识别介导细胞间通信的特定 L-R 对，进一步丰富了我们对 CCC 的理解。

事实上，以单细胞分辨率分析和可视化空间 CCC 对 scRNA-seq 数据提出了挑战。通常，CCC 被解释为不同细胞类型之间的 L-R 对。然而，DeepTalk 通过整合空间信息克服了这些挑战，允许在空间中选择相邻的共表达细胞对。这种方法提供了信息丰富的方法，可以从不同角度（包括在疾病病理生理学的背景下）分析和可视化 LRI 及其介导的 CCC。DeepTalk 在基准 ST 数据集上的出色表现证明了它能够破译健康和患病组织中的 CCC 机制。它通过揭示细胞间 LRI 及其在 CCC 中的功能，提供了对 CCC 的细致而精确的解释。此外，它可以预测和可视化单细胞分辨率下的细胞间通讯，并分析相关的 L-R 对，这对于理解生理和病理过程以及开发治疗方法至关重要。通过融合 scRNA-seq 和 ST 数据集，DeepTalk 提升了我们对 CCC 的解剖学理解，提供了更细致的见解；它还通过探索和可视化细胞间 LRI，提出了一种多方面的综合方法来理解 CCC。

本质上，DeepTalk 提供了一种重要的方法，它利用 GNN 和注意力机制来预测和说明由 L-R 对介导的 CCC。通过结合 scRNA-seq 和 ST 数据集，它增强了我们探索 CCC 的分析能力，最终提供对细胞相互作用的详细和准确的理解。尽管存在诸如长距离通信和多模态数据融合等挑战，但 DeepTalk 仍然是通过探测细胞间对话并以视觉方式呈现这些相互作用来解开 CCC 复杂性的关键工具。它的应用范围扩展到研究生理和病理过程，以及帮助开发创新的治疗方法。此外，整合其他组学数据，特别是由 10x Multiome 和数字空间分析等尖端技术生成的数据，可以进一步完善我们对 CCC 中空间控制的检查。通过融合多模态数据，我们可以更深入地理解驱动 CCC 的机制。为了推进 CCC 研究，DeepTalk 可以发展到涵盖空间约束和多模态数据集成，从而实现更精确、更详细的推理分析。

数据集预处理

对每个数据集执行了几个预处理步骤。使用 Scanpy 对 scRNA-seq 数据进行质量控制。根据几个标准对细胞进行过滤，以确保下游分析的质量。具体来说，线粒体基因表达百分比超过 20% 的细胞被排除在外，因为线粒体含量高可能表明应激或凋亡细胞。但是，需要注意的是，线粒体基因表达百分比阈值可以根据具体情况进行调整。总计数异常高或表达基因数量过多的细胞也被去除。根据每个数据集的特征，精心选择总计数和基因数量的具体阈值，以仅保留最高质量的细胞以供进一步分析。此外，Scanpy 的 filter_cells 和 filter_genes 功能被用于通过去除低质量的细胞和基因来进一步纯化数据集。对于 scRNA-seq 和 ST 数据集，表达矩阵的归一化是必不可少的。我们使用了 Scanpy 包中广泛使用的 normalize_total 函数来执行此规范化。归一化在数学上可以表示为：

其中是细胞j中基因i的原始计数，是标准化的表达值，T是标准化后计数的目标总和，确保所有细胞的一致性。[Math Processing Error]${\mathbf{X}}_{ij}${{{{\bf{X}}}}}_{{ij}}\hbox{`}[Math Processing Error]${\mathbf{X}}_{ij}\text{`}$

在 scRNA-seq 和 ST 数据的整合过程中，训练基因的选择至关重要。为了增强 ST 数据的鉴别能力，我们精心策划了一组标记基因，这些基因均匀分布在 scRNA-seq 数据中的不同细胞类型中作为训练基因。具体来说，我们利用 Scanpy 中的 rank_genes_groups 功能来识别特定细胞类型中表达最多的基因。在此之后，我们创建一个非冗余基因集，并将其与 ST 数据集中的基因列表相交。在任一数据集中记录零计数的基因被排除在我们的训练基因集中，从而保证只包含相关和表达的基因。此过程会产生一个包含“n”个基因的精细基因集，这将作为模型训练的基础。对于模型验证，我们采用留一法验证策略。具体来说，我们依次将精炼基因集中的每个基因指定为测试基因，而其余的 'n-1' 基因作为训练基因发挥作用。这个训练过程迭代了 “n” 次，每次都省略一个不同的基因，以确保每个基因都得到独立的预测评估。

DeepTalk 算法

DeepTalk 模型有两个组成部分：scRNA-seq 和 ST 数据集的整合（DeepTalk-Integration）和空间 CCC 预测（DeepTalk-CCC）。前者侧重于确定单细胞或基于点的 ST 数据集的细胞类型组成，而后者旨在预测受空间环境中的 L-R 对影响的空间介导 CCC。

scRNA-seq 与 ST 数据集的整合

基于注意力机制的 GNN 被用于整合 scRNA-seq 和 ST 数据集（补充图 20a）。该网络的任务是生成匹配的描述符，表示为，其中 ' D ' 表示特征空间的维数，确定特征向量中分量的长度或数量。这些描述符是通过初始特征之间的特征通信创建的，初始特征包含原始或最低限度处理的数据，例如转录组信息和细胞位置。最初，我们开发了一个点编码器，结合每个细胞的转录组数据和细胞位置，表示为。通过使用多层感知器 (MLP)，细胞位置被嵌入到高维向量中，表示为：[Math Processing Error]${\mathbf{f}}_i\in {\mathbb{R}}^D$i[Math Processing Error]$i$

其中表示从转录组获得的基因表达数据，表示细胞的位置信息。该点编码器允许 GNN 在后续推理阶段同时利用和。[Math Processing Error]${\mathbf{d}}_i$[Math Processing Error]${\mathbf{p}}_i$[Math Processing Error]${\mathbf{d}}_i$[Math Processing Error]${\mathbf{p}}_i$

随后，我们创建了一个整合两个组学的图，其中节点代表来自两个转录组的细胞。自边将每个细胞连接到同一组学中的所有其他细胞，而交叉边将细胞链接到具有不同组学的所有其他细胞。为了有效地传播信息，采用了消息传递方程，使信息能够沿着自边和交叉边传播。这种方法产生了一个多 GNN，其中每个节点都以高维状态开始。在每一层，更新的表示都是通过同时聚合来自图内所有节点的所有边的消息来计算的。[Math Processing Error]$i$[Math Processing Error]$i$

In the proposed framework, the intermediate representation of element [Math Processing Error]$i$ in the scRNA-seq A at layer [Math Processing Error]$l$ is denoted by [Math Processing Error]${\mathbf{x}}_{Ai}^{(l)}$. The message [Math Processing Error]${\mathbf{m}}_{\text{ε}\to i}$ represents the aggregation of information from all cells j:(i,j)\in \varepsilon \varepsilon \in \{{\varepsilon }_{{self}},\,{\varepsilon }_{{cross}}\} ij, such that {[Math Processing Error]$j:(i,j)\in \text{ε}$}, where [Math Processing Error]$\text{ε}\in \{{\text{ε}}_{self},{\text{ε}}_{cross}\}$. The residual message-passing update for all [Math Processing Error]$i$ in the scRNA-seq A can be expressed as follows:

where the concatenation operator [Math Processing Error]$[\cdot \text{||}\cdot ]$ is used for concatenation. A comparable update can be simultaneously applied to all the points in omics B. To create a hierarchical structure, a predetermined number of layers L with distinct parameters are linked together and the information is alternately aggregated along the self- and cross-edges; starting from [Math Processing Error]$l=1$, [Math Processing Error]$\text{ε}={\text{ε}}_{self}$ when [Math Processing Error]$l$ is an odd number and [Math Processing Error]$\text{ε}={\text{ε}}_{cross}$ when [Math Processing Error]$l$ is an even number. This approach enabled iterative aggregation along different edges, thereby facilitating effective representation learning.

The aggregation and computation of the message [Math Processing Error]${\mathbf{m}}_{\text{ε}\to i}$ were performed by an attention mechanism. The self- and cross-edges used self- and cross-attention, respectively. As in database retrieval, the query [Math Processing Error]${\mathbf{q}}_i$ was used to retrieve values [Math Processing Error]${\mathbf{v}}_j$ for specific elements based on their attributes, represented as keys [Math Processing Error]${\mathbf{k}}_j$. Thereafter, the message was computed by taking the weighted average of the retrieved values as follows:

The attention weight [Math Processing Error]$a_{ij}$ is calculated as the softmax of the key-query similarities and is represented as [Math Processing Error]$a_{ij}=\text{Softmax}({\mathbf{q}}_i^T{\mathbf{k}}_j)$. The key, query, and value are obtained by applying linear projections to the deep features of the GNN. Considering that the query point \left(Q,S\right)\in {\{A,B\}}^{2}i belongs to the scRNA-seq dataset Q and all source points reside in the ST dataset S, this relationship can be expressed as [Math Processing Error]$(Q,S)\in {\{A,B\}}^2$.

The projection parameters are specific to each layer [Math Processing Error]$l$; these parameters are learned and shared across all points in both datasets. Multi-head attention was employed to enhance the expressiveness of the model, enabling the representation of both geometric transformations and assignments. The resulting matching descriptors were obtained via linear projections as follows:

They were similarly obtained for points in B.

Creating individual representations for every potential match in a matrix of size n_cells × n_spots is impractical. Therefore, an alternative approach was adopted by representing the pairwise scores as a similarity matrix [Math Processing Error]$M\in {\mathbb{R}}^{ncells\times nspots}$ capturing the similarity of the matching descriptors.

where[Math Processing Error]$<\cdot ,\cdot >$ is the inner product. The matching descriptors are not normalized, and their magnitude may vary on a per-feature basis throughout the training process to reflect the confidence level of the predictions. To derive the mapping matrix, the following objective function was minimized with respect to M:

where [Math Processing Error]${\cos }_{\mathrm{s}\mathrm{i}\mathrm{m}}$ is the cosine similarity function and * indicates matrix slicing.

Spatial CCC prediction

During pretraining, we employed a random-walk strategy to generate pretraining subgraphs [Math Processing Error]$G_C$ for each node in the graph. This process involved masking and predicting nodes within the random walks, effectively capturing the graph’s overall connectivity patterns (Supplementary Fig. {g}_{c}\in {G}_{c} {g}_{c} {g}_{c}\,=\,({v}_{1},\,{v}_{2},\; {\ldots },\; {v}_{\left|{V}_{c}\right|}) |{V}_{c}| {g}_{c}20b). For each node v in the graph during pretraining (and for each node-pair during fine-tuning), we generated individual subgraphs denoted as [Math Processing Error]$g_c\in G_c$. Each subgraph [Math Processing Error]$g_c$ was encoded as a set of nodes represented by [Math Processing Error]$g_c=(v_1,v_2,\dots ,v_{\left|V_c\right|})$, where [Math Processing Error]$|V_c|$ denotes the number of nodes in [Math Processing Error]$g_c$.

We assigned a low-dimensional vector representation to each node v_i in the subgraph. This representation was obtained by mapping the attributes (such as gene expression data or cellular phenotypes) and the structure-based embedding of v_i using the function [Math Processing Error]$f_{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{r}}\text{(.)}$. The resulting stacked vector was denoted as [Math Processing Error]${\mathbf{h}}_i=W_e{f}_{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{r}}\left({\mathbf{v}}_i\right)$, where [Math Processing Error]$W_e$ is a learnable embedding matrix. Collectively, the node embeddings within the subgraph [Math Processing Error]$g_c$ were represented as [Math Processing Error]$H_c=({\mathbf{h}}_1,{\mathbf{h}}_2,\dots ,{\mathbf{h}}_{|V_c|})$. This flexible representation approach allowed us to incorporate both node and relation attributes into low-dimensional embeddings. Alternatively, these embeddings could also be initialized using the output embeddings from other global feature generation methods that capture the multi-relational graph structure. Specifically, for the initialization of node features in our study, we merged pretrained node representation vectors from node2vec with gene expression data acquired from cells.

For a subgraph [Math Processing Error]$g_c$, where [Math Processing Error]$V_c$ represents the set of nodes and [Math Processing Error]$H_c\in {\mathbb{R}}^{d\times |V_c|}$ denotes their corresponding global input embeddings, the main objective of contextual learning is to transform these global embeddings to reflect the most representative roles of the nodes within the structure of [Math Processing Error]${\mathrm{g}}_{\mathrm{c}}$. This transformation was achieved via a series of layers, with the model having the flexibility to incorporate multiple layers to account for higher-order relationships within the graph. To capture higher-order relational dependencies between nodes—including indirect and multi-step interactions—we introduced a semantic association matrix, denoted as [Math Processing Error]$\overline{A}$, which acts as an asymmetric weight matrix. This asymmetry originated from the different influences that the two cells may have on each other within a subgraph. The weights of the matrix [Math Processing Error]${\overline{A}}^k$ were iteratively learned in each translation layer [Math Processing Error]$k$ by considering the connectivity between nodes through the local context subgraph [Math Processing Error]$g_c$ and larger global graph G.

In the k + 1 translation layer, the semantic association matrix [Math Processing Error]${\overline{A}}^k\in {\mathbb{R}}^{|V_c|\times |V_c|}$ was updated via the transformation operation, which involves performing message passing across all nodes within the subgraph [Math Processing Error]${\mathrm{g}}_{\mathrm{c}}$ and updating the node embeddings [Math Processing Error]$H_c^k=({\mathbf{h}}_1^k,{\mathbf{h}}_2^k,\dots ,{\mathbf{h}}_{|V_c|}^k)$ to [Math Processing Error]$H_c^{k+1}$. The update process ensures that the embeddings capture the evolving representations of the nodes based on the contextual information derived from the message passing and relationship updates in the subgraph. Specifically, the updated node embeddings [Math Processing Error]$H_c^{k+1}$ are computed as follows:

Here, [Math Processing Error]$f_{\text{NN}}$ represents a non-linear function, and [Math Processing Error]$W_s\in {\mathbb{R}}^{d\times d}$ is a learnable transformation matrix.

The non-linear function and the transformation matrix were used to compute the corresponding entry [Math Processing Error]${\overline{A}}_{ij}^k$ in the semantic association matrix. To retain contextual embeddings from the previous step, we incorporate a residual connection. This ensures that global relations are preserved by passing the original global embeddings through the layers. For the two nodes [Math Processing Error]${\mathbf{v}}_i$ and [Math Processing Error]${\mathbf{v}}_j$ within the subgraph [Math Processing Error]$g_c$, the calculation of [Math Processing Error]${\overline{A}}_{ij}^k$ utilizes a multihead attention mechanism with [Math Processing Error]$N_h$ heads, allowing us to capture the relational dependencies within different subspaces. For each head, [Math Processing Error]${\overline{A}}_{ij}^k$ was computed as follows:

where the transformation matrices [Math Processing Error]$W_1$ and [Math Processing Error]$W_2$ are learnable parameters. By applying multiple translation layers, multiple embeddings were generated for each node within the subgraph. Considering the various embeddings in downstream tasks, the node embeddings learned from different layers [Math Processing Error]${\{{\mathbf{h}}_i^k\}}_{k=1,\dots ,K}$ were embedded into the contextual embedding [Math Processing Error]${\tilde{\mathbf{h}}}_i$ for each node. This aggregation was performed as follows:

After obtaining the embedding vectors [Math Processing Error]${\{{\tilde{\mathbf{h}}}_i\}}_{i=1\text{,}2\text{,...,}|V_c|}$ for the nodes within [Math Processing Error]$g_c$, these embeddings can be used as inputs for prediction tasks. During pretraining, a linear projection function was applied to the embeddings to predict the probabilities of the masked nodes. In the fine-tuning step, we utilized a single-layer feed-forward network with a softmax activation function for binary link prediction, facilitating predictions regarding the presence or absence of links between nodes.

Pretraining in the proposed model involves training a self-supervised node-prediction task. For each node in G, a node [Math Processing Error]$g_c$ with a diameter (the maximum shortest distance between any pair of nodes) was created using the aforementioned generation methods. Subsequently, a single node within the subgraph was randomly masked for prediction without altering the graph structure. Therefore, pretraining was accomplished by maximizing the probability of correctly predicting the masked node [Math Processing Error]${\mathbf{v}}_m$ based on the given context [Math Processing Error]$g_c$. The probability was computed in the following form:

where [Math Processing Error]$\theta$ represents the set of model parameters.

To fine-tune the model further, we focused on a contextualized link prediction task. Multiple fine-grained contexts were generated for each node pair considered for link prediction. During this stage, the model was trained to maximize the probability of observing a positive edge ([Math Processing Error]$e_p$) given its corresponding context ([Math Processing Error]$g_{cp}$). Simultaneously, the model learned to assign low probabilities to the negatively sampled edges ([Math Processing Error]$e_n$) and their associated contexts ([Math Processing Error]$g_{cn}$). The overall objective was constructed by summing over two subsets of training data: positive edges ([Math Processing Error]$D_p$) and negative edges ([Math Processing Error]$D_n$). By optimizing this objective, the model improved its ability to accurately predict the positive and negative edges.

The probability of an edge between two nodes, denoted by [Math Processing Error]$e=({\mathbf{v}}_i,{\mathbf{v}}_j)$, was calculated using the similarity score [Math Processing Error]$\text{S}({\mathbf{v}}_i,{\mathbf{v}}_j)$, which can be mathematically expressed as [Math Processing Error]$\text{S}({\mathbf{v}}_i,{\mathbf{v}}_j)=\text{σ}({\tilde{\mathbf{h}}}_i^T\cdot {\tilde{\mathbf{h}}}_j)$, where[Math Processing Error]${\tilde{\mathbf{h}}}_i$ and [Math Processing Error]${\tilde{\mathbf{h}}}_j$ are embeddings of [Math Processing Error]${\mathbf{v}}_i$ and [Math Processing Error]${\mathbf{v}}_j$, respectively. [Math Processing Error]$\text{σ}(\cdot )$ represents sigmoid function. The probability of an edge between two nodes was thereby calculated based on the similarity of their embeddings.

Definition of cell type for the ST dataset

To analyze the single-cell ST dataset, the cell type with the highest coefficient was assigned to each individual cell type. For the 10X Visium fluorescence dataset used in this study, squidpy.im.segment () was used to segment the tissue image. For the ST dataset, the maximum cell number ([Math Processing Error]$N_{cell}$) was defined for each spot, and [Math Processing Error]$N_{cell}$ was set to 20 based on a recent review⁷⁹. To determine the optimal combination (ω) of cells for each spot, the following function was used:

where [Math Processing Error]$\left[N_{\text{cell}}{\beta }_i\right]$ and [Math Processing Error]$\{N_{\text{cell}}{\beta }_i\}$ represent the integer and fractional parts of [Math Processing Error]$N_{cell}{\beta }_i$, respectively. Thereafter, a subset of cells ([Math Processing Error]$n={\sum }_{i=1}^k{\mathit{\omega }}_i$) was randomly selected from the total cell population (S) and the merged expression profile ([Math Processing Error]$\mathit{ϵ}$) of the cell was compared with the ground truth using the following function:

To assign the coordinates [Math Processing Error]$(x^{\mathrm{\prime }},y^{\mathrm{\prime }})$ to each sampled cell, we introduced a probabilistic distribution based on the ratio (R) of the same cell type in neighboring spots, allowing us to determine the probability of locating a cell in a specific region within a spot. The distribution was calculated using the following equation:

where [Math Processing Error]$d_{min}$ represents the minimum spatial distance to the closest neighbor spot and [Math Processing Error]$\alpha \in (0,1]$ and [Math Processing Error]$\theta \in (0,360]$ represent the weight for dmin and angle toward the spot center ([Math Processing Error]$x_0$, [Math Processing Error]$y_0$), respectively. Notably, [Math Processing Error]$\theta$ is determined by the following probability equation:

where [Math Processing Error]$q$ is the [Math Processing Error]$\mathrm{q}\mathrm{t}\mathrm{h}$ neighbor spot among Q spots. Practically, Q was set to 4, dividing the space around the spot into four quadrants and filtering the nearest neighbor in each quadrant. After determining [Math Processing Error]$\theta$, the corresponding neighbor spot ([Math Processing Error]$x^{\mathrm{\prime }},y^{\mathrm{\prime }}$) was selected to calculate the probabilistic distribution of α using the following equation:

where [Math Processing Error]$R_{x_0,y_0}$ and [Math Processing Error]$R_{x^{\mathrm{\prime }},y^{\mathrm{\prime }}}$ represent the ratios of the given cell type in each spot to its neighboring spot, respectively. These optimal cellular combinations were integrated for all spots to reconstruct the single-cell resolution ST dataset for the spot-based ST dataset.

Definition of the CCC score

To generate the cell–cell distance matrix D, the spatial coordinates of individual cells were used to calculate their Euclidean distances. However, to focus on nearby secretion and paracrine signaling within a specific range, we only considered the cells that were 200 μm apart⁷⁹. Subsequently, the K-nearest neighbors (KNN) algorithm was applied to select the K closest cells from the distance matrix D, aiding the construction of a cell graph network by establishing connections between the selected cells. The receptor was used as the query node to ensure the biological relevance of the identified CCCs. A random walk algorithm was employed to filter and score the downstream-activated transcription factors (TFs). Thus, the TFs activated in response to a queried receptor were identified; consequently, we considered only cells with activated TFs as receptor cells. This approach provides a more accurate representation of the intercellular information transfer and communication as it reflects the actual cellular response to signaling events.

To ascertain the co-expression of a specific ligand-receptor pair between the sender cells (of type A) expressing a given ligand and the receiver cells (of type B) expressing the corresponding receptor in the cell graph network, we computed the number of cell–cell pairs ([Math Processing Error]$C_{A_i,B_j}^0$) exhibiting this ligand-receptor interaction. This involved identifying the direct neighboring nodes (1-hop away) of the sender cells expressing ligand i and the receiver cells expressing receptor j. For each ligand-receptor interaction between cell types A and B, there may be distinct cell–cell pair counts.

A permutation test was employed to gauge the significance of these observed counts. This entailed randomly reassigning cell labels and recomputing the ligand-receptor interaction counts. This procedure was iterated (Z) times, generating a background distribution [Math Processing Error]$C=C_{A_i,B_j}^1,C_{A_i,B_j}^2,{\dots ,C}_{A_i,B_j}^Z$. The P-value was then determined by juxtaposing the observed cell–cell pair counts for the specified ligand-receptor interactions against this background distribution.

Mathematically, the P-value was computed as follows:

P-values less than 0.05 were considered statistically significant and were used to calculate the CCC score of the ligand-receptor interaction from senders to receivers. This score was computed as [Math Processing Error]$S_{A_i,B_j}=\sqrt{L_{A_i}\times R_{B_j}}$, where [Math Processing Error]$L_{A_i}$ is the gene expression of the ligand [Math Processing Error]$L$ in cell [Math Processing Error]$i$ of cell type A and [Math Processing Error]$R_{B_j}$ is the gene expression of the receptor [Math Processing Error]$R$ in cell [Math Processing Error]$j$ of cell type B.

Benchmark metrics

Benchmark metrics for integration methods

Five metrics were used to evaluate the integration methods, one of the metrics being the Pearson correlation coefficient (PCC), which is calculated using the following equation:

where [Math Processing Error]${\mathbf{x}}_i$ and [Math Processing Error]${\tilde{\mathbf{x}}}_i$ represent the spatial expression vectors of the i-th gene in the ground truth and the predicted results, respectively. Similarly, [Math Processing Error]$u_i$ and [Math Processing Error]${\tilde{u}}_i$ correspond to the average expression value of the i-th gene in the ground truth and the predicted result, respectively, and [Math Processing Error]${\text{σ}}_i$ and [Math Processing Error]${\widetilde{\text{σ}}}_i$ represent the standard deviation of the spatial expression of the i-th gene in the ground truth and the predicted result, respectively. While evaluating a specific gene, a higher PCC value indicates a higher prediction accuracy for that gene. The PCC value measures the degree of linear association between the ground truth and predicted results for a particular gene.

The evaluation of the integration methods also used the structural similarity index (SSIM). To prepare the data for SSIM calculation, the expression matrix was scaled by adjusting the expression values of each gene to lie in the range of 0–1 as follows:

where [Math Processing Error]${\mathrm{x}}_{\mathrm{i}\mathrm{j}}$ denotes the expression of the i-th gene in the j-th spot, and M is the total number of spots. Normalizing the expression values facilitated a consistent and comparable evaluation of integration methods using the SSIM metric. After scaling the gene expression values between 0 and 1, the SSIM value for each gene was calculated using the following equation:

To calculate the SSIM value for each gene, we utilized the same definitions of [Math Processing Error]$u_i$, [Math Processing Error]${\tilde{u}}_i$,[Math Processing Error]${\text{σ}}_i$ and [Math Processing Error]${\widetilde{\text{σ}}}_i$ as in the calculation of the PCC value, but for the scaled gene expression. Additionally, C₁ and C₂ were introduced as constant values and set to 0.01 and 0.03, respectively. The term [Math Processing Error]$\mathrm{c}\mathrm{o}\mathrm{v}({\mathbf{x}}_i,{\tilde{\mathbf{x}}}_i)$ represents the covariance between the expression vectors of the i-th gene in the ground truth ([Math Processing Error]${\mathbf{x}}_i\text{`}$) and the predicted result ([Math Processing Error]${\tilde{\mathbf{x}}}_i\text{`}$). Similar to the PCC value, a higher SSIM value indicates a higher level of prediction accuracy for a given gene.

The z-score for the spatial expression of each gene was calculated for all spots. The root mean square error (RMSE) was computed as follows:

where [Math Processing Error]${\mathbf{z}}_{ij}$ and [Math Processing Error]${\tilde{\mathbf{z}}}_{ij}$ are the z-scores of the spatial expression of the i-th gene in the j-th spot in the ground truth and predicted results, respectively. For a given gene, a lower RMSE value indicates a higher level of prediction accuracy.

The Jensen–Shannon divergence (JSD) uses the relative information entropy, particularly the Kullback–Leibler divergence, to quantify the difference between the two distributions. To calculate the spatial distribution probability of each gene, the following steps were performed:

To calculate the spatial distribution probability of each gene, we assign [Math Processing Error]${\mathbf{x}}_{ij}$ as the expression value of the i-th gene in the j-th spot, where M is the total number of spots and [Math Processing Error]${\mathbf{P}}_{ij}$ is the distribution probability of the i-th gene in the j-th spot. After calculating the spatial distribution probability, the JSD value for each gene was evaluated using the following equations:

where [Math Processing Error]${\mathbf{P}}_{\mathbf{i}}$ and [Math Processing Error]${\tilde{\mathbf{P}}}_i$ represent the spatial distribution probability vectors of the i-th gene in the ground truth and predicted result, respectively; [Math Processing Error]$\text{KL}({\mathbf{a}}_i||{\mathbf{b}}_i)$ denotes the Kullback–Leibler divergence between the two probability distributions [Math Processing Error]${\mathbf{a}}_i$ and [Math Processing Error]${\mathbf{b}}_i$; [Math Processing Error]${\mathbf{a}}_{ij}$ and [Math Processing Error]${\mathbf{b}}_{ij}$ represent the predicted and real probabilities of the i-th gene in the j-th spot, respectively. For a given gene, a lower JSD value indicates a higher level of prediction accuracy.

To evaluate the relative accuracy of the integration methods for each dataset, an accuracy score (AS) was defined by combining the PCC, SSIM, RMSE, and JSD metrics. For a given dataset, the average PCC, SSIM, RMSE, and JSD values were calculated for all the genes predicted by each integration method. Subsequently, the PCC and SSIM values of the integration methods were sorted in ascending order to obtain [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{P}\mathrm{C}\mathrm{C}}$ and [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}}$, respectively. The integration method with the highest PCC/SSIM value had [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{P}\mathrm{C}\mathrm{C}/\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}}$ equal to N, whereas the method with the lowest PCC/SSIM value had the [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{P}\mathrm{C}\mathrm{C}/\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}}$ value of 1. Similarly, the RMSE and JSD values of the integration methods were sorted in the descending order to obtain [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}$ and [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{J}\mathrm{S}\mathrm{D}}$, respectively. The integration method with the highest RMSE/JSD value had [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}/\mathrm{J}\mathrm{S}\mathrm{D}}$ = 1, whereas the method with the lowest RMSE/JSD value had [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}/\mathrm{J}\mathrm{S}\mathrm{D}}$ = N. Finally, the average values of [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{P}\mathrm{C}\mathrm{C}}$, [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}}$, [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}$, and [Math Processing Error]${\mathrm{R}\mathrm{A}\mathrm{N}\mathrm{K}}_{\mathrm{J}\mathrm{S}\mathrm{D}}$ were determined to obtain the AS value for each integration method as follows:

The method with the highest AS value exhibited the best performance among the integration methods.

Benchmark metrics for the CCC prediction method

The Wasserstein distance concept was introduced as a metric to assess the spatial communication tendency in a specific ligand-receptor (L-R) pair. Here, L and R represent the gene expression distributions of the ligand and receptor, respectively. For brevity, we refer to the actual Wasserstein distances between these distributions as [Math Processing Error]$d_{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}$. To establish a comparative baseline, we constructed random gene expression distributions, [Math Processing Error]$L_r$ and [Math Processing Error]$R_r$, by permuting the coordinates of each data point in L and R. By repeatedly permuting (1000 times in our case) and calculating the Wasserstein distance between [Math Processing Error]$L_r$ and [Math Processing Error]$R_r$, denoted as d_simulation, we obtained a set of d_simulation values. Subsequently, the spatial communication tendency was quantified by computing the ratio of [Math Processing Error]$d_{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}$ to the mean of the d_simulation set, referred to as [Math Processing Error]$d_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}}$. This ratio serves as a measure of the spatial communication tendency specific to the L-R pair under consideration.

By increasing the number of permutations (n), we constructed a null distribution of [Math Processing Error]$d_{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}$ using the d_simulation set. This null distribution was then utilized in a one-sided permutation test to derive a P-value, indicating the significance of the observed spatial communication tendency. Additionally, left- and right-sided P-values were calculated to distinguish between short- and long-range communications. To quantify the consistency between expected and observed spatial distance tendencies, we employed the DES metric, where a higher value signifies better consistency⁶⁹. Based on their [数学处理错误] $d_{\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}}$ and P-values, short- and long-range communications were ranked to form expected communication lists, [数学处理错误] [数学处理错误] [数学处理错误] [数学处理错误] [ 数学处理错误] [数学处理错误] [数学处理错误] [数学处理错误]$L_s$ and $L_l$, respectively. Subsequently, we extracted communications from the CCC tool’s results and created observed communication lists, S, for each cell type pair. These lists were denoted as $S_n$ and $S_f$, for nearby and distant cell type pairs, respectively. To compute the DES for a particular cell type pair, we considered weighted P-value proportions ($P_{\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}$ and $P_{\mathrm{u}\mathrm{n}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}$) while iterating through the expected communication list. The presence or absence of communication in the observed list determined the addition or subtraction of the corresponding weights, respectively. This approach allowed us to assess the consistency between expected and observed communications for a given cell type pair. A similar methodology was applied to compute the DES for distant cell type pairs. The $P_{\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}$ and $P_{\mathrm{u}\mathrm{n}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}$ values for the j-th interaction in $L_s$ are defined as follows:

where n represents the total number of matched interactions between [数学处理错误] $S_n$ and [数学处理错误] [数学处理错误]$L_s$. The DES represents the maximum deviation of ($P_{\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}-P_{\mathrm{u}\mathrm{n}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}$) from 0, providing a quantitative measure of consistency between expected and observed spatial interaction tendencies.

Comparison with other methods

To compare the predictive performance of DeepTalk with that of other methods for predicting the spatial distribution of undetected transcripts, we used a dataset comprising 45 paired ST and scRNA-seq datasets curated by Li et al.³⁵. These datasets were generated using various techniques, including FISH, osmFISH, seqFISH, MERFISH, STARmap, ISS, EXseq, BaristaSeq, ST, 10X Visium, Slide-seq, Seq-scope, and HDST. STARmap and seqFISH+ST datasets were employed to assess the accuracy of DeepTalk and other methods for cell type decomposition. For the single-cell ST dataset, the cells were separated into distinct groups based on fixed spatial distances and combined to create simulated spots, resulting in a reference dataset. The performances of Tangram, Cell2location, SpatialDWLS, RCTD, Stereoscope, DestVI, and SPOTlight in predicting cell-type compositions within each spot were evaluated by comparing them with true cell-type compositions, using metrics such as PCC, SSIM, RMSE, JSD, and AS. By utilizing a benchmark dataset comprising the MERFISH, 10X Visium, and ST datasets, we compared the performance of DeepTalk with that of other methods for inferring CCC, including CellCall, CellChat, CellChatV2, CellPhoneDB, CellPhoneDBV3, ICELLNET, iTALK, SingleCellSignalR, Giotto, stLearn, Connectome, NicheNet, COMMOT. All methods were evaluated using their default parameters. For the comparison of NICHES and Scrabin, two methods for inferring CCC at the single-cell resolution, we utilize the same ground-truth ligand-receptor pairs obtained from OmniPath⁸⁰ for this analysis.

Visualize the CCC patterns using UMAP

To visualize the CCC patterns using UMAP, we predicted CCC events mediated by various L-R pairs at single-cell resolution. Each predicted event was assigned a quantitative score reflecting the communication strength, resulting in a matrix where rows represent distinct CCC events, and columns correspond to unique L-R pairs. For dimensionality reduction and visualization, we employed Scanpy, a robust tool for single-cell analysis. Initially, we scaled the data using sc.pp.scale() to normalize the feature values. This was followed by principal component analysis (PCA) using sc.tl.pca(), which helped reduce the dimensionality of the dataset while preserving its main structure. Next, we constructed a neighborhood graph using sc.pp.neighbors(), which identifies cells that are close to each other in the high-dimensional space. This step is crucial for subsequent manifold learning techniques. Finally, we used sc.tl.umap() to craft the UMAP visualizations, thereby enabling the depiction of intricate CCC patterns within a two-dimensional framework.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.