Solving olympiad geometry without human demonstrations
不借助人类演示解决奥林匹克几何题

Proving theorems showcases the mastery of logical reasoning and the ability to search through an infinitely large space of actions towards a target, signifying a remarkable problem-solving skill. Since the 1950s (refs. ^6,7), the pursuit of better theorem-proving capabilities has been a constant focus of artificial intelligence (AI) research⁸. Mathematical olympiads are the most reputed theorem-proving competitions in the world, with a similarly long history dating back to 1959, playing an instrumental role in identifying exceptional talents in problem solving. Matching top human performances at the olympiad level has become a notable milestone of AI research^2,3,4.
证明定理展示了逻辑推理的掌握和在向目标进发的无限大的行动空间中搜索的能力，标志着卓越的解决问题技能。自 1950 年代以来，追求更好的定理证明能力一直是人工智能（AI）研究的持续焦点。数学奥林匹克是世界上最有声望的定理证明竞赛，同样有着长达 1959 年的悠久历史，对于识别解决问题中的异常人才起着重要作用。在奥林匹克级别上匹配顶尖人类表现已成为 AI 研究的一个显著里程碑。

Theorem proving is difficult for learning-based methods because training data of human proofs translated into machine-verifiable languages are scarce in most mathematical domains. Geometry stands out among other olympiad domains because it has very few proof examples in general-purpose mathematical languages such as Lean⁹ owing to translation difficulties unique to geometry^1,5. Geometry-specific languages, on the other hand, are narrowly defined and thus unable to express many human proofs that use tools beyond the scope of geometry, such as complex numbers (Extended Data Figs. 3 and 4). Overall, this creates a data bottleneck, causing geometry to lag behind in recent progress that uses human demonstrations^2,3,4. Current approaches to geometry, therefore, still primarily rely on symbolic methods and human-designed, hard-coded search heuristics^{10,11,12,13,14}.
定理证明对于基于学习的方法来说是困难的，因为大多数数学领域中，将人类证明翻译成机器可验证语言的训练数据非常稀缺。几何在其他奥林匹克领域中脱颖而出，因为它在通用数学语言（如Lean）中的证明示例非常少，这是由于几何独有的翻译困难。另一方面，专门的几何语言定义独特，因此无法表达许多使用超出几何范围的工具（如复数）的人类证明（扩展数据图3和4）。总的来说，这造成了数据瓶颈，导致几何在使用人类演示的最近进展中落后。因此，当前的几何方法仍主要依赖于符号方法和人类设计的、硬编码的搜索启发式。

We present an alternative method for theorem proving using synthetic data, thus sidestepping the need for translating human-provided proof examples. We focus on Euclidean plane geometry and exclude topics such as geometric inequalities and combinatorial geometry. By using existing symbolic engines on a diverse set of random theorem premises, we extracted 100 million synthetic theorems and their proofs, many with more than 200 proof steps, four times longer than the average proof length of olympiad theorems. We further define and use the concept of dependency difference in synthetic proof generation, allowing our method to produce nearly 10 million synthetic proof steps that construct auxiliary points, reaching beyond the scope of pure symbolic deduction. Auxiliary construction is geometry’s instance of exogenous term generation, representing the infinite branching factor of theorem proving, and widely recognized in other mathematical domains as the key challenge to proving many hard theorems^1,2. Our work therefore demonstrates a successful case of generating synthetic data and learning to solve this key challenge. With this solution, we present a general guiding framework and discuss its applicability to other domains in Methods section ‘AlphaGeometry framework and applicability to other domains’.
我们提出了一种使用合成数据进行定理证明的替代方法，从而避免了翻译人类提供的证明示例的需求。我们专注于欧几里得平面几何，并排除了几何不等式和组合几何等主题。通过在一系列随机定理前提上使用现有的符号引擎，我们提取了1亿个合成定理及其证明，其中许多证明步骤超过200步，是奥林匹克定理平均证明长度的四倍。我们进一步定义并使用合成证明生成中的依赖差异概念，使我们的方法能够产生近1000万个合成证明步骤，这些步骤构建辅助点，超出了纯符号推导的范围。辅助构造是几何学中外源术语生成的实例，代表了定理证明的无限分支因子，并且在其他数学领域被广泛认为是证明许多难定理的关键挑战。因此，我们的工作展示了一个成功的合成数据生成和学习解决这一关键挑战的案例。有了这个解决方案，我们提出了一个通用的指导框架，并在方法部分“AlphaGeometry框架及其适用性于其他领域”中讨论了其适用性。

We pretrain a language model on all generated synthetic data and fine-tune it to focus on auxiliary construction during proof search, delegating all deduction proof steps to specialized symbolic engines. This follows standard settings in the literature, in which language models such as GPT-f (ref. ¹⁵), after being trained on human proof examples, can generate exogenous proof terms as inputs to fast and accurate symbolic engines such as nlinarith or ring^2,3,16, using the best of both worlds. Our geometry theorem prover AlphaGeometry, illustrated in Fig. 1, produces human-readable proofs, substantially outperforms the previous state-of-the-art geometry-theorem-proving computer program and approaches the performance of an average IMO gold medallist on a test set of 30 classical geometry problems translated from the IMO as shown in Fig. 2.
我们在所有生成的合成数据上预训练一个语言模型，并对其进行微调，以便在证明搜索过程中专注于辅助结构，将所有演绎证明步骤委托给专门的符号引擎。这遵循文献中的标准设置，在该设置中，像 GPT-f（参考文献 ¹⁵ ）这样的语言模型在接受人类证明示例的训练后，可以生成作为输入的外源证明项，以便快速且准确的符号引擎，如 nlinarith 或 ring ^2,3,16 ，使用两全其美的策略。我们的几何定理证明器 AlphaGeometry，如图 1 所示，生成人类可读的证明，大大超越了之前最先进的几何定理证明计算机程序，并在一组从 IMO 翻译的 30 个经典几何问题的测试集上接近平均 IMO 金牌获得者的表现，如图 2 所示。

The top row shows how AlphaGeometry solves a simple problem. a, The simple example and its diagram. b, AlphaGeometry initiates the proof search by running the symbolic deduction engine. The engine exhaustively deduces new statements from the theorem premises until the theorem is proven or new statements are exhausted. c, Because the symbolic engine fails to find a proof, the language model constructs one auxiliary point, growing the proof state before the symbolic engine retries. The loop continues until a solution is found. d, For the simple example, the loop terminates after the first auxiliary construction “D as the midpoint of BC”. The proof consists of two other steps, both of which make use of the midpoint properties: “BD = DC” and “B, D, C are collinear”, highlighted in blue. The bottom row shows how AlphaGeometry solves the IMO 2015 Problem 3 (IMO 2015 P3). e, The IMO 2015 P3 problem statement and diagram. f, The solution of IMO 2015 P3 has three auxiliary points. In both solutions, we arrange language model outputs (blue) interleaved with symbolic engine outputs to reflect their execution order. Note that the proof for IMO 2015 P3 in f is greatly shortened and edited for illustration purposes. Its full version is in the Supplementary Information.
顶部行展示了 AlphaGeometry 如何解决一个简单问题。a, 简单示例及其图表。b, AlphaGeometry 通过运行符号演绎引擎启动证明搜索。引擎从定理前提中彻底推导出新的声明，直到证明定理或新的声明被耗尽。c, 由于符号引擎未能找到证明，语言模型构建了一个辅助点，在符号引擎重试之前增长证明状态。循环继续直到找到解决方案。d, 对于简单示例，循环在第一个辅助构造“D 为 BC 的中点”后终止。证明包括其他两个步骤，两者都利用了中点的属性：“BD = DC”和“B, D, C 是共线的”，以蓝色突出显示。底部行展示了 AlphaGeometry 如何解决 IMO 2015 问题 3（IMO 2015 P3）。e, IMO 2015 P3 问题声明和图表。f, IMO 2015 P3 的解决方案有三个辅助点。在两种解决方案中，我们安排语言模型输出（蓝色）与符号引擎输出交错，以反映它们的执行顺序。请注意，f 中的 IMO 2015 P3 的证明被大大缩短并编辑用于说明目的。其完整版本在补充信息中。

Full size image

The test benchmark includes official IMO problems from 2000 to the present that can be represented in the geometry environment used in our work. Human performance is estimated by rescaling their IMO contest scores between 0 and 7 to between 0 and 1, to match the binary outcome of failure/success of the machines. For example, a contestant’s score of 4 out of 7 will be scaled to 0.57 problems in this comparison. On the other hand, the score for AlphaGeometry and other machine solvers on any problem is either 0 (not solved) or 1 (solved). Note that this is only an approximate comparison with humans on classical geometry, who operate on natural-language statements rather than narrow, domain-specific translations. Further, the general IMO contest also includes other types of problem, such as geometric inequality or combinatorial geometry, and other domains of mathematics, such as algebra, number theory and combinatorics.
测试基准包括从 2000 年到现在的官方 IMO 问题，这些问题可以在我们工作中使用的几何环境中表示。通过将他们的 IMO 竞赛分数从 0 到 7 重新缩放到 0 到 1 之间，来估计人类的表现，以匹配机器的失败/成功的二元结果。例如，一个参赛者的得分为 7 分中的 4 分，将在这个比较中缩放到 0.57 问题。另一方面，AlphaGeometry 和其他机器求解器在任何问题上的得分要么是 0（未解决），要么是 1（已解决）。注意，这只是与在经典几何上操作自然语言陈述而不是狭窄的、特定领域翻译的人类的大致比较。此外，一般的 IMO 竞赛还包括其他类型的问题，如几何不等式或组合几何，以及其他数学领域，如代数、数论和组合学。

Source Data 源数据

Full size image

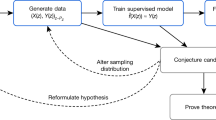
Our method for generating synthetic data is shown in Fig. 3. We first sample a random set of theorem premises, serving as the input to the symbolic deduction engine to generate its derivations. A full list of actions used for this sampling can be found in Extended Data Table 1. In our work, we sampled nearly 1 billion of such premises in a highly parallelized setting, described in Methods. Note that we do not make use of any existing theorem premises from human-designed problem sets and sampled the eligible constructions uniformly randomly.
我们生成合成数据的方法如图 3 所示。我们首先随机抽取一个定理前提集合，作为输入到符号推导引擎以生成其推导。用于此抽样的完整动作列表可以在扩展数据表 1 中找到。在我们的工作中，我们在一个高度并行化的设置中抽样了近 10 亿这样的前提。注意，我们没有使用任何来自人类设计的问题集的现有定理前提，并且均匀随机地抽样了合格的构造。

a, We first sample a large set of random theorem premises. b, We use the symbolic deduction engine to obtain a deduction closure. This returns a directed acyclic graph of statements. For each node in the graph, we perform traceback to find its minimal set of necessary premise and dependency deductions. For example, for the rightmost node ‘HA ⊥ BC’, traceback returns the green subgraph. c, The minimal premise and the corresponding subgraph constitute a synthetic problem and its solution. In the bottom example, points E and D took part in the proof despite being irrelevant to the construction of HA and BC; therefore, they are learned by the language model as auxiliary constructions.
a, 我们首先抽样一大批随机定理前提。b, 我们使用符号推理引擎获得一个推理闭包。这将返回一个有向无环图的陈述。对图中的每个节点，我们执行回溯以找到其最小的必要前提和依赖推理集。例如，对于最右边的节点‘HA ⊥ BC’，回溯返回绿色子图。c, 最小前提和相应的子图构成一个合成问题及其解决方案。在底部的例子中，尽管 E 点和 D 点与构建 HA 和 BC 无关，但它们仍参与了证明；因此，它们被语言模型学习为辅助构造。

Full size image

Next we use a symbolic deduction engine on the sampled premises. The engine quickly deduces new true statements by following forward inference rules as shown in Fig. 3b. This returns a directed acyclic graph of all reachable conclusions. Each node in the directed acyclic graph is a reachable conclusion, with edges connecting to its parent nodes thanks to the traceback algorithm described in Methods. This allows a traceback process to run recursively starting from any node N, at the end returning its dependency subgraph G(N), with its root being N and its leaves being a subset of the sampled premises. Denoting this subset as P, we obtained a synthetic training example (premises, conclusion, proof) = (P, N, G(N)).
接下来我们在抽样的前提上使用符号推理引擎。该引擎通过遵循前向推理规则快速推导出新的真实陈述，如图 3b 所示。这将返回一个包含所有可达结论的有向无环图。有向无环图中的每个节点都是一个可达结论，通过回溯算法连接到其父节点。这允许从任何节点 N 开始递归运行回溯过程，最终返回其依赖子图 G(N)，其根是 N，其叶子是抽样前提的一个子集。将这个子集表示为 P，我们获得了一个合成训练示例（前提，结论，证明）=（P，N，G(N)）。

In geometry, the symbolic deduction engine is deductive database (refs. ^10,17), with the ability to efficiently deduce new statements from the premises by means of geometric rules. DD follows deduction rules in the form of definite Horn clauses, that is, Q(x) ← P₁(x),…, P_k(x), in which x are points objects, whereas P₁,…, P_k and Q are predicates such as ‘equal segments’ or ‘collinear’. A full list of deduction rules can be found in ref. ¹⁰. To widen the scope of the generated synthetic theorems and proofs, we also introduce another component to the symbolic engine that can deduce new statements through algebraic rules (AR), as described in Methods. AR is necessary to perform angle, ratio and distance chasing, as often required in many olympiad-level proofs. We included concrete examples of AR in Extended Data Table 2. The combination DD + AR, which includes both their forward deduction and traceback algorithms, is a new contribution in our work and represents a new state of the art in symbolic reasoning in geometry.
在几何学中，符号推理引擎是一个演绎数据库（参考文献 ^10,17 ），能够通过几何规则有效地从前提中推导出新的陈述。DD 遵循确定性霍恩子句形式的推理规则，即 Q(x) ← P ₁ (x),…, P _k (x)，其中 x 是点对象，而 P ₁ ，…, P _k 和 Q 是如‘等长线段’或‘共线’等谓词。完整的推理规则列表可以在参考文献 ¹⁰ 中找到。为了扩大生成的合成定理和证明的范围，我们还向符号引擎引入了另一个组件，该组件可以通过代数规则（AR）推导出新的陈述，如方法中所述。AR 是执行角度、比率和距离追踪所必需的，这在许多奥林匹克级别的证明中经常需要。我们在扩展数据表 2 中包含了 AR 的具体示例。DD + AR 的组合，包括它们的前向推理和追溯算法，是我们工作中的一个新贡献，并代表了几何中符号推理的新艺术状态。

So far, the generated proofs consist purely of deduction steps that are already reachable by the highly efficient symbolic deduction engine DD + AR. To solve olympiad-level problems, however, the key missing piece is generating new proof terms. In the above algorithm, it can be seen that such terms form the subset of P that N is independent of. In other words, these terms are the dependency difference between the conclusion statement and the conclusion objects. We move this difference from P to the proof so that a generative model that learns to generate the proof can learn to construct them, as illustrated in Fig. 3c. Such proof steps perform auxiliary constructions that symbolic deduction engines are not designed to do. In the general theorem-proving context, auxiliary construction is an instance of exogenous term generation, a notable challenge to all proof-search algorithms because it introduces infinite branching points to the search tree. In geometry theorem proving, auxiliary constructions are the longest-standing subject of study since inception of the field in 1959 (refs. ^6,7). Previous methods to generate them are based on hand-crafted templates and domain-specific heuristics^8,9,10,11,12, and are, therefore, limited by a subset of human experiences expressible in hard-coded rules. Any neural solver trained on our synthetic data, on the other hand, learns to perform auxiliary constructions from scratch without human demonstrations.
到目前为止，生成的证明完全由高效的符号演绎引擎 DD + AR 已经能够达到的推理步骤组成。然而，要解决奥林匹克级别的问题，关键缺失部分是生成新的证明项。在上述算法中，可以看到这样的项形成了 P 的一个子集，而 N 是独立的。换句话说，这些项是结论声明和结论对象之间的依赖差异。我们将这种差异从 P 移至证明中，以便学习生成证明的生成模型能够学会构建它们，如图 3c 所示。这样的证明步骤执行辅助构造，这是符号演绎引擎设计之外的工作。在一般定理证明上下文中，辅助构造是外源项生成的一个实例，这对所有证明搜索算法来说是一个显著的挑战，因为它为搜索树引入了无限的分支点。在几何定理证明中，辅助构造自该领域 1959 年创立以来就是研究的最长久的主题（参考文献 ^6,7 ）。以前生成它们的方法基于手工制作的模板和特定领域的启发式 ^8,9,10,11,12 ，因此，受限于可用硬编码规则表达的人类经验的子集。另一方面，任何在我们的合成数据上训练的神经求解器，学会了从零开始执行辅助构造，而无需人类演示。

The transformer¹⁸ language model is a powerful deep neural network that learns to generate text sequences through next-token prediction, powering substantial advances in generative AI technology. We serialize (P, N, G(N)) into a text string with the structure ‘<premises><conclusion><proof>’. By training on such sequences of symbols, a language model effectively learns to generate the proof, conditioning on theorem premises and conclusion.
变压器 ¹⁸ 语言模型是一个强大的深度神经网络，通过下一个令牌预测学习生成文本序列，推动了生成性 AI 技术的重大进步。我们将(P, N, G(N))序列化成具有‘’结构的文本字符串。通过在这样的符号序列上训练，语言模型有效地学会了生成证明，条件是定理的前提和结论。

On a high level, proof search is a loop in which the language model and the symbolic deduction engine take turns to run, as shown in Fig. 1b,c. Proof search terminates whenever the theorem conclusion is found or when the loop reaches a maximum number of iterations. The language model is seeded with the problem statement string and generates one extra sentence at each turn, conditioning on the problem statement and past constructions, describing one new auxiliary construction such as “construct point X so that ABCX is a parallelogram”. Each time the language model generates one such construction, the symbolic engine is provided with new inputs to work with and, therefore, its deduction closure expands, potentially reaching the conclusion. We use beam search to explore the top k constructions generated by the language model and describe the parallelization of this proof-search algorithm in Methods.
在高层次上，证明搜索是一个循环，在这个循环中，语言模型和符号推理引擎轮流运行，如图 1b,c 所示。当找到定理结论或循环达到最大迭代次数时，证明搜索终止。语言模型以问题陈述字符串为种子，并在每个回合生成一个额外的句子，根据问题陈述和过去的构造条件，描述一个新的辅助构造，例如“构造点 X，使得 ABCX 是一个平行四边形”。每次语言模型生成这样一个构造时，符号引擎就会得到新的输入来工作，因此，其推理闭包扩展，潜在地达到结论。我们使用束搜索来探索语言模型生成的前 k 个构造，并在方法中描述了这种证明搜索算法的并行化。

An olympiad-level benchmark for geometry
几何学奥林匹克级基准

Existing benchmarks of olympiad mathematics do not cover geometry because of a focus on formal mathematics in general-purpose languages^1,9, whose formulation poses great challenges to representing geometry. Solving these challenges requires deep expertise and large research investment that are outside the scope of our work, which focuses on a methodology for theorem proving. For this reason, we adapted geometry problems from the IMO competitions since 2000 to a narrower, specialized environment for classical geometry used in interactive graphical proof assistants^13,17,19, as discussed in Methods. Among all non-combinatorial geometry-related problems, 75% can be represented, resulting in a test set of 30 classical geometry problems. Geometric inequality and combinatorial geometry, for example, cannot be translated, as their formulation is markedly different to classical geometry. We include the full list of statements and translations for all 30 problems in the Supplementary Information. The final test set is named IMO-AG-30, highlighting its source, method of translation and its current size.
现有的奥林匹克数学基准测试不包括几何，因为它们通常关注于通用语言中的形式数学 ^1,9 ，其公式化对于表示几何提出了巨大挑战。解决这些挑战需要深厚的专业知识和大量的研究投入，这超出了我们工作的范围，我们的工作重点是定理证明的方法论。因此，我们从 2000 年以来的 IMO 竞赛中选择了几何问题，适应于一个更狭窄、专门用于交互式图形证明助手中的经典几何环境 ^13,17,19 ，如方法部分所讨论。在所有非组合几何相关问题中，75%可以被表示，结果是一个包含 30 个经典几何问题的测试集。例如，几何不等式和组合几何不能被翻译，因为它们的公式化与经典几何截然不同。我们在补充信息中包含了所有 30 个问题的完整陈述和翻译。最终的测试集被命名为 IMO-AG-30，突出了其来源、翻译方法和当前的大小。

Geometry theorem provers in the literature fall into two categories. The first category is computer algebra methods, which treats geometry statements as polynomial equations of its point coordinates. Proving is accomplished with specialized transformations of large polynomials. Gröbner bases²⁰ and Wu’s method²¹ are representative approaches in this category, with theoretical guarantees to successfully decide the truth value of all geometry theorems in IMO-AG-30, albeit without a human-readable proof. Because these methods often have large time and memory complexity, especially when processing IMO-sized problems, we report their result by assigning success to any problem that can be decided within 48 h using one of their existing implementations¹⁷.
文献中的几何定理证明器分为两类。第一类是计算机代数方法，它将几何陈述视为其点坐标的多项式方程。证明是通过大型多项式的专门变换来完成的。Gröbner 基 ²⁰ 和 Wu 的方法 ²¹ 是这一类别中的代表性方法，理论上保证能成功决定 IMO-AG-30 中所有几何定理的真值，尽管没有人类可读的证明。因为这些方法通常具有很大的时间和内存复杂性，特别是在处理 IMO 规模的问题时，我们通过将成功分配给任何可以在 48 小时内使用它们现有的实现 ¹⁷ 决定的问题来报告它们的结果。

AlphaGeometry belongs to the second category of solvers, often described as search/axiomatic or sometimes ‘synthetic’ methods. These methods treat the problem of theorem proving as a step-by-step search problem using a set of geometry axioms. Thanks to this, they typically return highly interpretable proofs accessible to human readers. Baselines in this category generally include symbolic engines equipped with human-designed heuristics. For example, Chou et al. provided 18 heuristics such as “If OA ⊥ OB and OA = OB, construct C on the opposite ray of OA such that OC = OA”, besides 75 deduction rules for the symbolic engine. Large language models^22,23,24 such as GPT-4 (ref. ²⁵) can be considered to be in this category. Large language models have demonstrated remarkable reasoning ability on a variety of reasoning tasks^26,27,28,29. When producing full natural-language proofs on IMO-AG-30, however, GPT-4 has a success rate of 0%, often making syntactic and semantic errors throughout its outputs, showing little understanding of geometry knowledge and of the problem statements itself. Note that the performance of GPT-4 performance on IMO problems can also be contaminated by public solutions in its training data. A better GPT-4 performance is therefore still not comparable with other solvers. In general, search methods have no theoretical guarantee in their proving performance and are known to be weaker than computer algebra methods¹³.
AlphaGeometry 属于第二类求解器，通常被描述为搜索/公理化或有时被称为“合成”方法。这些方法将定理证明问题视为一个使用一组几何公理的逐步搜索问题。因此，它们通常返回对人类读者来说易于解释的证明。这一类的基准通常包括配备了人为设计的启发式规则的符号引擎。例如，Chou 等人提供了 18 种启发式规则，如“如果 OA ⊥ OB 且 OA = OB，在 OA 的对面射线上构造 C 使得 OC = OA”，除此之外还有 75 条为符号引擎设计的推理规则。大型语言模型 ^22,23,24 ，如 GPT-4（参考 ²⁵ ）可以被认为属于这一类。大型语言模型在各种推理任务上展示了卓越的推理能力 ^26,27,28,29 。然而，在生成 IMO-AG-30 的完整自然语言证明时，GPT-4 的成功率为 0%，其输出通常充满了语法和语义错误，显示出对几何知识和问题陈述本身几乎没有理解。需要注意的是，GPT-4 在 IMO 问题上的表现也可能因其训练数据中的公开解决方案而受到污染。因此，更好的 GPT-4 表现仍然无法与其他求解器相比。总的来说，搜索方法在其证明性能上没有理论保证，且已知比计算机代数方法要弱 ¹³ 。

Synthetic data generation rediscovers known theorems and beyond
合成数据生成重新发现已知定理及其之外的内容。

We find that our synthetic data generation can rediscover some fairly complex theorems and lemmas known to the geometry literature, as shown in Fig. 4, despite starting from randomly sampled theorem premises. This can be attributed to the use of composite actions described in Extended Data Table 1, such as ‘taking centroid’ or ‘taking excentre’, which—by chance—sampled a superset of well-known theorem premises, under our large-scale exploration setting described in Methods. To study the complexity of synthetic proofs, Fig. 4 shows a histogram of synthetic proof lengths juxtaposed with proof lengths found on the test set of olympiad problems. Although the synthetic proof lengths are skewed towards shorter proofs, a small number of them still have lengths up to 30% longer than the hardest problem in the IMO test set. We find that synthetic theorems found by this process are not constrained by human aesthetic biases such as being symmetrical, therefore covering a wider set of scenarios known to Euclidean geometry. We performed deduplication as described in Methods, resulting in more than 100 millions unique theorems and proofs, and did not find any IMO-AG-30 theorems, showing that the space of possible geometry theorems is still much larger than our discovered set.
我们发现，尽管从随机采样的定理前提开始，我们的合成数据生成可以重新发现一些几何文献中已知的相当复杂的定理和引理，如图 4 所示。这可以归因于使用了扩展数据表 1 中描述的复合动作，例如“取质心”或“取外心”，这些动作偶然地采样了一组已知定理前提的超集，在我们描述的大规模探索设置下。为了研究合成证明的复杂性，图 4 显示了一个合成证明长度的直方图，与奥林匹亚问题测试集中发现的证明长度并列。尽管合成证明的长度倾向于较短的证明，但仍有少数证明的长度比 IMO 测试集中最难问题的长度长达 30%。我们发现，通过这一过程发现的合成定理不受人类审美偏见的限制，例如对称性，因此涵盖了更广泛的已知欧几里得几何场景。我们按照方法描述执行了重复数据删除，结果产生了超过 1 亿个独特的定理和证明，并且没有发现任何 IMO-AG-30 定理，表明可能的几何定理空间仍然比我们发现的集合要大得多。

Of the generated synthetic proofs, 9% are with auxiliary constructions. Only roughly 0.05% of the synthetic training proofs are longer than the average AlphaGeometry proof for the test-set problems. The most complex synthetic proof has an impressive length of 247 with two auxiliary constructions. Most synthetic theorem premises tend not to be symmetrical like human-discovered theorems, as they are not biased towards any aesthetic standard.
在生成的合成证明中，9%带有辅助构造。只有大约 0.05%的合成训练证明比测试集问题的平均 AlphaGeometry 证明更长。最复杂的合成证明具有令人印象深刻的 247 的长度，并带有两个辅助构造。大多数合成定理前提不倾向于像人类发现的定理那样对称，因为它们不偏向于任何审美标准。

Source Data 源数据

Full size image

Language model pretraining and fine-tuning
语言模型预训练和微调

We first pretrained the language model on all 100 million synthetically generated proofs, including ones of pure symbolic deduction. We then fine-tuned the language model on the subset of proofs that requires auxiliary constructions, accounting for roughly 9% of the total pretraining data, that is, 9 million proofs, to better focus on its assigned task during proof search.
我们首先在所有 1 亿个合成生成的证明上预训练了语言模型，包括纯符号推理的证明。然后，我们在需要辅助构造的证明子集上对语言模型进行了微调，这部分大约占总预训练数据的 9%，即 900 万个证明，以便在证明搜索过程中更好地专注于其分配的任务。

The performance of ten different solvers on the IMO-AG-30 benchmark is reported in Table 1, of which eight, including AlphaGeometry, are search-based methods. Besides prompting GPT-4 to produce full proofs in natural language with several rounds of reflections and revisions, we also combine GPT-4 with DD + AR as another baseline to enhance its deduction accuracy. To achieve this, we use detailed instructions and few-shot examples in the prompt to help GPT-4 successfully interface with DD + AR, providing auxiliary constructions in the correct grammar. Prompting details of baselines involving GPT-4 is included in the Supplementary Information.
在 IMO-AG-30 基准测试中报告了十种不同求解器的性能，见表 1，其中八种包括 AlphaGeometry 在内是基于搜索的方法。除了提示 GPT-4 用几轮反思和修订产生完整的自然语言证明外，我们还将 GPT-4 与 DD + AR 结合作为另一个基线以提高其推理准确性。为此，我们在提示中使用详细指令和少数示例来帮助 GPT-4 成功地与 DD + AR 接口，以正确的语法提供辅助构造。涉及 GPT-4 的基线提示细节包含在补充信息中。

AlphaGeometry achieves the best result, with 25 problems solved in total. The previous state of the art (Wu’s method) solved ten problems, whereas the strongest baseline (DD + AR + human-designed heuristics) solved 18 problems, making use of the algebraic reasoning engine developed in this work and the human heuristics designed by Chou et al.¹⁷. To match the test time compute of AlphaGeometry, this strongest baseline makes use of 250 parallel workers running for 1.5 h, each attempting different sets of auxiliary constructions suggested by human-designed heuristics in parallel, until success or timeout. Other baselines such as Wu’s method or the full-angle method are not affected by parallel compute resources as they carry out fixed, step-by-step algorithms until termination.
AlphaGeometry 取得了最佳结果，总共解决了 25 个问题。以前的最佳方法（Wu 的方法）解决了十个问题，而最强基线（DD + AR + 人为设计的启发式）解决了 18 个问题，利用了本工作开发的代数推理引擎和 Chou 等人设计的人类启发式 ¹⁷ 。为了匹配 AlphaGeometry 的测试时间计算，这个最强基线使用了 250 个并行工作器运行 1.5 小时，每个工作器尝试由人为设计的启发式并行建议的不同组辅助构造，直到成功或超时。其他基线如 Wu 的方法或全角方法不受并行计算资源的影响，因为它们执行固定的、逐步的算法直到终止。

Measuring the improvements made on top of the base symbolic deduction engine (DD), we found that incorporating algebraic deduction added seven solved problems to a total of 14 (DD + AR), whereas the language model’s auxiliary construction remarkably added another 11 solved problems, resulting in a total of 25. As reported in Extended Data Fig. 6, we find that, using only 20% of the training data, AlphaGeometry still achieves state-of-the-art results with 21 problems solved. Similarly, using less than 2% of the search budget (beam size of 8 versus 512) during test time, AlphaGeometry can still solve 21 problems. On a larger and more diverse test set of 231 geometry problems, which covers textbook exercises, regional olympiads and famous theorems, we find that baselines in Table 1 remain at the same performance rankings, with AlphaGeometry solving almost all problems (98.7%), whereas Wu’s method solved 75% and DD + AR + human-designed heuristics solved 92.2%, as reported in Extended Data Fig. 6b.
在基础符号演绎引擎（DD）之上测量改进效果时，我们发现加入代数演绎增加了 7 个已解决问题，总数达到 14 个（DD + AR），而语言模型的辅助构建显著增加了另外 11 个已解决问题，总数达到 25 个。如扩展数据图 6 所报告的，我们发现，仅使用 20%的训练数据，AlphaGeometry 仍然实现了解决 21 个问题的最先进结果。同样，测试时使用不到 2%的搜索预算（束大小为 8 对比 512），AlphaGeometry 仍能解决 21 个问题。在一个更大且更多样化的 231 个几何问题测试集上，涵盖了教科书练习、地区奥林匹克竞赛和著名定理，我们发现表 1 中的基线保持相同的性能排名，其中 AlphaGeometry 几乎解决了所有问题（98.7%），而吴氏方法解决了 75%，DD + AR + 人为设计的启发式解决了 92.2%，如扩展数据图 6b 所报告的。

Notably, AlphaGeometry solved both geometry problems of the same year in 2000 and 2015, a threshold widely considered difficult to the average human contestant at the IMO. Further, the traceback process of AlphaGeometry found an unused premise in the translated IMO 2004 P1, as shown in Fig. 5, therefore discovering a more general version of the translated IMO theorem itself. We included AlphaGeometry solutions to all problems in IMO-AG-30 in the Supplementary Information and manually analysed some notable AlphaGeometry solutions and failures in Extended Data Figs. 2–5. Overall, we find that AlphaGeometry operates with a much lower-level toolkit for proving than humans do, limiting the coverage of the synthetic data, test-time performance and proof readability.
值得注意的是，AlphaGeometry 解决了 2000 年和 2015 年同年的两个几何问题，这是一个被广泛认为对于国际数学奥林匹克竞赛的平均参赛者来说难度较大的门槛。此外，AlphaGeometry 的追溯过程在翻译的 2004 年国际数学奥林匹克竞赛 P1 题中发现了一个未使用的前提，如图 5 所示，因此发现了翻译的国际数学奥林匹克定理本身的一个更通用版本。我们在补充信息中包含了 AlphaGeometry 对 IMO-AG-30 所有问题的解决方案，并在扩展数据图 2-5 中手动分析了一些值得注意的 AlphaGeometry 解决方案和失败案例。总的来说，我们发现 AlphaGeometry 使用的证明工具箱比人类的要低级得多，限制了合成数据的覆盖范围、测试时的性能和证明的可读性。

Left, top to bottom, the IMO 2004 P1 stated in natural language, its translated statement and AlphaGeometry solution. Thanks to the traceback algorithm necessary to extract the minimal premises, AlphaGeometry identifies a premise unnecessary for the proof to work: O does not have to be the midpoint of BC for P, B, C to be collinear. Right, top, the original theorem diagram; bottom, the generalized theorem diagram, in which O is freed from its midpoint position and P still stays on line BC. Note that the original problem requires P to be between B and C, a condition where the generalized theorem and solution does not guarantee.
从左到右，自上而下，IMO 2004 P1 用自然语言陈述，其翻译陈述和 AlphaGeometry 解决方案。多亏了用于提取最小前提的回溯算法，AlphaGeometry 识别出一个对证明工作不必要的前提：O 不必是 BC 的中点，以使 P、B、C 共线。右边，上面是原始定理图；下面，是推广定理图，在此图中 O 不再局限于中点位置，而 P 仍然位于 BC 线上。请注意，原始问题要求 P 位于 B 和 C 之间，这是一个推广定理和解决方案不保证的条件。

Full size image

Human expert evaluation of AlphaGeometry outputs
AlphaGeometry 输出的人类专家评估

Because AlphaGeometry outputs highly interpretable proofs, we used a simple template to automatically translate its solutions to natural language. To obtain an expert evaluation in 2000 and 2015, during which AlphaGeometry solves all geometry problems and potentially passes the medal threshold, we submit these solutions to the USA IMO team coach, who is experienced in grading mathematical olympiads and has authored books for olympiad geometry training. AlphaGeometry solutions are recommended to receive full scores, thus passing the medal threshold of 14/42 in the corresponding years. We note that IMO tests also evaluate humans under three other mathematical domains besides geometry and under human-centric constraints, such as no calculator use or 4.5-h time limits. We study time-constrained settings with 4.5-h and 1.5-h limits for AlphaGeometry in Methods and report the results in Extended Data Fig. 1.
由于 AlphaGeometry 输出高度可解释的证明，我们使用了一个简单的模板来自动将其解决方案翻译成自然语言。为了在 2000 年和 2015 年获得专家评估，期间 AlphaGeometry 解决了所有几何问题并有可能通过奖牌门槛，我们将这些解决方案提交给美国 IMO 团队教练，他在评分数学奥林匹克方面经验丰富，并且为奥林匹克几何训练著有书籍。AlphaGeometry 的解决方案被推荐获得满分，从而通过相应年份的 14/42 的奖牌门槛。我们注意到，IMO 测试还在几何以外的其他三个数学领域评估人类，并且受到以人为中心的限制，例如不使用计算器或 4.5 小时的时间限制。我们在方法中研究了 4.5 小时和 1.5 小时限制下的 AlphaGeometry，并在扩展数据图 1 中报告结果。

Learning to predict the symbolic engine’s output improves the language model’s auxiliary construction
学习预测符号引擎的输出可以提高语言模型的辅助构建能力

In principle, auxiliary construction strategies must depend on the details of the specific deduction engine they work with during proof search. We find that a language model without pretraining only solves 21 problems. This suggests that pretraining on pure deduction proofs generated by the symbolic engine DD + AR improves the success rate of auxiliary constructions. On the other hand, a language model without fine-tuning also degrades the performance but not as severely, with 23 problems solved compared with AlphaGeometry’s full setting at 25.
原则上，辅助构建策略必须依赖于它们在证明搜索过程中工作的特定推理引擎的细节。我们发现，一个没有预训练的语言模型只解决了 21 个问题。这表明，在符号引擎 DD + AR 生成的纯推理证明上进行预训练，可以提高辅助构建的成功率。另一方面，一个没有微调的语言模型也会降低性能，但不是很严重，与 AlphaGeometry 的完整设置相比，解决了 23 个问题。

Hard problems are reflected in AlphaGeometry proof length
困难问题反映在 AlphaGeometry 证明长度上

Figure 6 measures the difficulty of solved problems using public scores of human contestants at the IMO and plots them against the corresponding AlphaGeometry proof lengths. The result shows that, for the three problems with the lowest human score, AlphaGeometry also requires exceptionally long proofs and the help of language-model constructions to reach its solution. For easier problems (average human score > 3.5), however, we observe no correlation (p = −0.06) between the average human score and AlphaGeometry proof length.
图 6 通过使用 IMO 人类参赛者的公开分数来衡量解决问题的难度，并将它们与相应的 AlphaGeometry 证明长度进行对比。结果显示，对于人类得分最低的三个问题，AlphaGeometry 也需要异常长的证明和语言模型构建的帮助才能找到解决方案。然而，对于较容易的问题（平均人类得分>3.5），我们观察到平均人类得分与 AlphaGeometry 证明长度之间没有相关性（p = -0.06）。

Among the solved problems, 2000 P6, 2015 P3 and 2019 P6 are the hardest for IMO participants. They also require the longest proofs from AlphaGeometry. For easier problems, however, there is little correlation between AlphaGeometry proof length and human score.
在解决的问题中，2000 P6、2015 P3 和 2019 P6 对 IMO 参与者来说是最难的。它们也需要来自 AlphaGeometry 的最长证明。然而，对于较容易的问题，AlphaGeometry 证明长度与人类得分之间几乎没有相关性。

Source Data 源数据

Full size image

AlphaGeometry is the first computer program to surpass the performance of the average IMO contestant in proving Euclidean plane geometry theorems, outperforming strong computer algebra and search baselines. Notably, we demonstrated through AlphaGeometry a neuro-symbolic approach for theorem proving by means of large-scale exploration from scratch, sidestepping the need for human-annotated proof examples and human-curated problem statements. Our method to generate and train language models on purely synthetic data provides a general guiding framework for mathematical domains that are facing the same data-scarcity problem.
AlphaGeometry 是第一个在证明欧几里得平面几何定理方面超越平均国际数学奥林匹克竞赛选手表现的计算机程序，其性能超过了强大的计算机代数和搜索基线。值得注意的是，我们通过 AlphaGeometry 展示了一种神经符号方法，用于通过从零开始的大规模探索来证明定理，从而避免了对人类注释的证明示例和人类策划的问题陈述的需求。我们在纯合成数据上生成和训练语言模型的方法为面临同样数据稀缺问题的数学领域提供了一个通用指导框架。

Geometry representation 几何表示

General-purpose formal languages such as Lean³¹ still require a large amount of groundwork to describe most IMO geometry problems at present. We do not directly address this challenge as it requires deep expertise and substantial research outside the scope of theorem-proving methodologies. To sidestep this barrier, we instead adopted a more specialized language used in GEX¹⁰, JGEX¹⁷, MMP/Geometer¹³ and GeoLogic¹⁹, a line of work that aims to provide a logical and graphical environment for synthetic geometry theorems with human-like non-degeneracy and topological assumptions. Examples of this language are shown in Fig. 1d,f. Owing to its narrow formulation, 75% of all IMO geometry problems can be adapted to this representation. In this type of geometry environment, each proof step is logically and numerically verified and can also be evaluated by a human reader as if it is written by IMO contestants, thanks to the highly natural grammar of the language. To cover more expressive algebraic and arithmetic reasoning, we also add integers, fractions and geometric constants to the vocabulary of this language. We do not push further for a complete solution to geometry representation as it is a separate and extremely challenging research topic that demands substantial investment from the mathematical formalization community.
诸如 Lean ³¹ 这样的通用形式语言目前仍需要大量的基础工作来描述大多数 IMO 几何问题。我们没有直接解决这一挑战，因为它需要深厚的专业知识和超出定理证明方法论范围的大量研究。为了绕过这一障碍，我们改为采用了一种在 GEX ¹⁰ 、JGEX ¹⁷ 、MMP/Geometer ¹³ 和 GeoLogic ¹⁹ 中使用的更专业的语言，这一系列工作旨在为具有类人非退化性和拓扑假设的合成几何定理提供逻辑和图形环境。该语言的示例显示在图 1d,f 中。由于其狭窄的表述，75% 的所有 IMO 几何问题都可以适应这种表示。在这种类型的几何环境中，每个证明步骤都经过逻辑和数值验证，也可以由人类读者评估，就好像它是由 IMO 参赛者编写的一样，这得益于该语言的高度自然语法。为了覆盖更多表达式的代数和算术推理，我们还在这种语言的词汇中添加了整数、分数和几何常数。我们没有进一步推动几何表示的完整解决方案，因为这是一个单独的且极具挑战性的研究主题，需要数学形式化社区的大量投资。

Sampling consistent theorem premises
采样一致的定理前提

We developed a constructive diagram builder language similar to that used by JGEX¹⁷ to construct one object in the premise at a time, instead of freely sampling many premises that involve several objects, therefore avoiding the generation of a self-contradicting set of premises. An exhaustive list of construction actions is shown in Extended Data Table 1. These actions include constructions to create new points that are related to others in a certain way, that is, collinear, incentre/excentre etc., as well as constructions that take a number as its parameter, for example, “construct point X such that given a number α, ∠ABX = α”. One can extend this list with more sophisticated actions to describe a more expressive set of geometric scenarios, improving both the synthetic data diversity and the test-set coverage. A more general and expressive diagram builder language can be found in ref. ³². We make use of a simpler language that is sufficient to describe problems in IMO-AG-30 and can work well with the symbolic engine DD.
我们开发了一种构造性图表构建语言，类似于 JGEX ¹⁷ 使用的语言，该语言一次构造一个前提中的对象，而不是自由抽样涉及多个对象的许多前提，因此避免了生成一组自相矛盾的前提。构造动作的详尽列表显示在扩展数据表 1 中。这些动作包括构造以某种方式与其他点相关的新点，即，共线、内心/外心等，以及以数字为参数的构造，例如，“构造点 X，使得给定一个数字α，∠ABX = α”。可以通过更复杂的动作扩展此列表，以描述更具表现力的几何场景集，提高合成数据的多样性和测试集的覆盖率。更通用和表达力更强的图表构建语言可以在参考文献 ³² 中找到。我们使用一种更简单的语言，足以描述 IMO-AG-30 中的问题，并且可以很好地与符号引擎 DD 配合使用。

The symbolic deduction engine
符号推理引擎

The core functionality of the engine is deducing new true statements given the theorem premises. Deduction can be performed by means of geometric rules such as ‘If X then Y’, in which X and Y are sets of geometric statements such as ‘A, B, C are collinear’. We use the method of structured DD^10,17 for this purpose as it can find the deduction closure in just seconds on standard non-accelerator hardware. To further enhance deduction, we also built into AlphaGeometry the ability to perform deduction through AR. AR enable proof steps that perform angle/ratio/distance chasing. Detailed examples of AR are shown in Extended Data Table 2. Such proof steps are ubiquitous in geometry proofs, yet not covered by geometric rules. We expand the Gaussian elimination process implemented in GeoLogic¹⁹ to find the deduction closure for all possible linear operators in just seconds. Our symbolic deduction engine is an intricate integration of DD and AR, which we apply alternately to expand the joint closure of known true statements until expansion halts. This process typically finishes within a few seconds to at most a few minutes on standard non-accelerator hardware.
引擎的核心功能是在给定定理前提的情况下推导出新的真实陈述。推理可以通过几何规则来执行，例如“如果 X，则 Y”，其中 X 和 Y 是一组几何陈述，如“A、B、C 是共线的”。我们使用结构化 DD ^10,17 的方法来实现这一目的，因为它可以在标准非加速硬件上仅用几秒钟就找到推理闭包。为了进一步增强推理，我们还在 AlphaGeometry 中构建了通过 AR 进行推理的能力。AR 使得执行角度/比率/距离追踪的证明步骤成为可能。AR 的详细示例显示在扩展数据表 2 中。这样的证明步骤在几何证明中无处不在，但几何规则并未涵盖。我们扩展了在 GeoLogic ¹⁹ 中实现的高斯消元过程，以在仅几秒钟内为所有可能的线性运算符找到推理闭包。我们的符号推理引擎是 DD 和 AR 的复杂整合，我们交替应用它们来扩展已知真实陈述的联合闭包，直到扩展停止。这个过程通常在几秒钟到最多几分钟内在标准非加速硬件上完成。

Algebraic reasoning 代数推理

There has not been a complete treatment for algebraic deduction in the literature of geometry theorem proving. For example, in iGeoTutor¹², Z3 (ref. ³³) is used to handle arithmetic inferences but algebraic manipulations are not covered. DD (ref. ¹⁷) handles algebraic deductions by expressing them under a few limited deduction rules, therefore, it is unable to express more complex manipulations, leaving arithmetic inferences not covered. The most general treatment so far is a process similar that in ref. ³⁴ for angle-only theorem discovery and implemented in GeoLogic¹⁹ for both angle and ratios. We expanded this formulation to cover all reasoning about angles, ratios and distances between points and also arithmetic reasoning with geometric constants such as ‘pi’ or ‘1:2’. Concrete examples of algebraic reasoning are given in Extended Data Table 2.
在几何定理证明的文献中，对代数推理尚未有完整的处理。例如，在 iGeoTutor ¹² 中，使用 Z3 (参考文献 ³³ ) 来处理算术推理，但没有涵盖代数操作。DD (参考文献 ¹⁷ ) 通过在几个有限的推理规则下表达它们来处理代数推理，因此，它无法表达更复杂的操作，留下算术推理未被涵盖。到目前为止，最通用的处理是一个类似于参考文献 ³⁴ 中的仅角度定理发现的过程，并在 GeoLogic ¹⁹ 中实现，用于角度和比率。我们扩展了这种公式化，以涵盖关于角度、比率和点之间距离的所有推理，以及与几何常数（如“π”或“1:2”）的算术推理。在扩展数据表 2 中给出了代数推理的具体示例。

On a high level, we first convert the input linear equations to a matrix of their coefficients. In particular, we create a coefficient matrix A ∈ R^M×N in which N is the number of variables and M is the number of input equations. In geometry, any equality is of the form a − b = c − d ⇔ a − b − c + d = 0. For example, the angle equality ∠ABC = ∠XYZ is represented as s(AB) − s(BC) = s(XY) − s(YZ), in which s(AB) is the angle between AB and the x-direction, modulo pi. Similarly, ratios AB:CD = EF:GH are represented as log(AB) − log(CD) = log(EF) − log(GH), in which log(AB) is the log of the length of segment AB. For distances, each variable is a (point, line) pair, representing a specific point on a specific line.
在高层次上，我们首先将输入的线性方程转换为其系数的矩阵。具体来说，我们创建一个系数矩阵 A ∈ R ^M×N ，其中 N 是变量的数量，M 是输入方程的数量。在几何学中，任何等式都是 a − b = c − d ⇔ a − b − c + d = 0 的形式。例如，角度等式 ∠ABC = ∠XYZ 表示为 s(AB) − s(BC) = s(XY) − s(YZ)，其中 s(AB) 是 AB 与 x 方向之间的角度，模 pi。同样，比例 AB:CD = EF:GH 表示为 log(AB) − log(CD) = log(EF) − log(GH)，其中 log(AB) 是线段 AB 长度的对数。对于距离，每个变量是一个（点，线）对，代表特定线上的特定点。

Because all equalities are of the form ‘a − b − c + d = 0’, we populate the row for each equality with values +1, −1, −1, +1 at columns corresponding to variables a, b, c and d. Running Gaussian elimination on A returns a new matrix with leading 1s at each of the columns, essentially representing each variable as a unique linear combination of all remaining variables. As an example, suppose we have ‘a − b = b − c’, ‘d − c = a − d’ and ‘b − c = c − e’ as input equalities, running the Gaussian elimination process (denoted GE in the following equation) returns the following result:
因为所有等式都是 ‘a − b − c + d = 0’ 的形式，我们在对应于变量 a, b, c 和 d 的列中为每个等式的行填充值 +1, −1, −1, +1。在 A 上运行高斯消元法会返回一个新矩阵，每列的前导 1s 本质上代表每个变量作为所有剩余变量的唯一线性组合。例如，假设我们有输入等式 ‘a − b = b − c’、‘d − c = a − d’ 和 ‘b − c = c − e’，运行高斯消元过程（在以下方程中表示为 GE）返回以下结果：

From this result, we can deterministically and exhaustively deduce all new equalities by checking if x₁ = x₂ or x₁ − x₂ = x₂ − x₃ or x₁ − x₂ = x₃ − x₄, in which {x₁, x₂, x₃, x₄} is any 4-permutation of all variables. In the above Gaussian Elimination, for example, AR deduced that b = d from the three input equalities. To handle geometric constants such as ‘0.5 pi’ or ‘5:12’, we included ‘pi’ and ‘1’ as default variables to all coefficient matrices.
从这个结果中，我们可以通过检查 x ₁ = x ₂ 或 x ₁ − x ₂ = x ₂ − x ₃ 或 x ₁ − x ₂ = x ₃ − x ₄ ，其中 {x ₁ , x ₂ , x ₃ , x ₄ } 是所有变量的任意 4-排列，来确定性地和穷尽地推导出所有新的等式。在上述高斯消元中，例如，AR 从三个输入等式中推导出 b = d。为了处理几何常数如 ‘0.5 pi’ 或 ‘5:12’，我们将 ‘pi’ 和 ‘1’ 作为所有系数矩阵的默认变量。

Deductive database implementation
推理数据库实现

Unlike the original implementation of DD, we use a graph data structure to capture the symmetries of geometry, rather than using strings of canonical forms. With a graph data structure, we captured not only the symmetrical permutations of function arguments but also the transitivity of equality, collinearity and concyclicity. This graph data structure bakes into itself some deduction rules explicitly stated in the geometric rule list used in DD. These deduction rules from the original list are therefore not used anywhere in exploration but implicitly used and explicitly spelled out on-demand when the final proof is serialized into text.
与 DD 的原始实现不同，我们使用图数据结构来捕捉几何的对称性，而不是使用规范形式的字符串。通过图数据结构，我们不仅捕获了函数参数的对称排列，还捕获了等式、共线性和共圆性的传递性。这种图数据结构将一些在 DD 中使用的几何规则列表中明确声明的推理规则内置于其中。因此，原始列表中的这些推理规则在探索中没有被使用，但在最终证明被序列化成文本时，会被隐式使用并明确说明。

Traceback to find minimal proofs
追溯以找到最小证明

Each deduction step needs to be coupled with a traceback algorithm, which returns the minimal set of immediate ancestor statements that is necessary to deduce the conclusion statement of the step. This is the core building block for extracting proof graphs and minimal premises described in the main text. A minimal-premise-extraction algorithm is necessary to avoid superfluous auxiliary constructions that contribute to the proof through unnecessary transitivity. For example, ‘a = b’ and ‘b = c’ might not be necessary if ‘a = c’ can be obtained directly through other reasoning chains.
每个推理步骤都需要与一个追溯算法结合，该算法返回为了推导出该步骤的结论陈述所必需的最小直接祖先陈述集合。这是提取证明图和主文中描述的最小前提的核心构建块。为了避免通过不必要的传递性贡献证明的多余辅助构造，需要一个最小前提提取算法。例如，如果‘a = c’可以通过其他推理链直接获得，那么‘a = b’和‘b = c’可能不是必需的。

Traceback for geometric-rule deduction
几何规则推导的追溯

To do this, we record the equality transitivity graph. For example, if ‘a = b’, ‘b = c’, ‘c = d’ and ‘a = d’ are deduced, which results in nodes a, b, c and d being connected to the same ‘equality node’ e, we maintain a graph within e that has edges [(a, b), (b, c), (c, d), (a, d)]. This allows the traceback algorithm to perform a breadth-first search to find the shortest path of transitivity of equality between any pair of variables among a, b, c and d. For collinearity and concyclicity, however, the representation is more complex. In these cases, hypergraphs G(V, E) with 3-edges or 4-edges are used as the equality transitivity graph. The traceback is now equivalent to finding a minimum spanning tree (denoted MST in the following equation) for the target set S of nodes (three collinear nodes or four concyclic nodes) whose weight is the cardinality of the union of its hyperedges e′:
为此，我们记录等式传递性图。例如，如果推导出‘a = b’、‘b = c’、‘c = d’和‘a = d’，则结果是节点 a、b、c 和 d 被连接到同一个‘等式节点’e，我们在 e 内维护一个有边[(a, b), (b, c), (c, d), (a, d)]的图。这允许回溯算法执行广度优先搜索，以找到在 a、b、c 和 d 之间的任何变量对之间的等式传递性的最短路径。然而，对于共线性和共圆性，表示更为复杂。在这些情况下，使用具有 3 边或 4 边的超图 G(V, E)作为等式传递性图。现在的回溯等同于为目标节点集 S（三个共线节点或四个共圆节点）找到一个最小生成树（在以下方程中表示为 MST），其权重是其超边 e′的并集的基数：

Such optimization is NP-hard, as it is a reduction from the decision version of vertex cover. We simply use a greedy algorithm in this case to find a best-effort minimum spanning tree.
这种优化是 NP 难的，因为它是从顶点覆盖的决策版本的简化。在这种情况下，我们简单地使用贪心算法来找到一个最佳努力的最小生成树。

Traceback for algebraic deduction
代数推导的回溯

Traceback through Gaussian elimination can be done by recognizing that it is equivalent to a mixed integer linear programming problem. Given the coefficient matrix of input equations A constructed as described in the previous sections and a target equation with coefficients vector b ∈ R^N, we determine the minimal set of premises for b by defining non-negative integer decision vectors x, y ∈ Z^M and solve the following mixed-integer linear programming problem:
通过高斯消元进行回溯可以通过认识到它等同于一个混合整数线性规划问题来完成。给定如前节所述构造的输入方程的系数矩阵 A 和一个目标方程的系数向量 b ∈ R ^N ，我们通过定义非负整数决策向量 x, y ∈ Z ^M 并解决以下混合整数线性规划问题来确定 b 的最小前提集：

The minimum set of immediate parent nodes for the equality represented by b will be the ith equations (ith rows in A) whose corresponding decision value (x_i − y_i) is non-zero.
由 b 表示的等式所对应的最小一组直接父节点将是第 i 个方程（A 中的第 i 行），其对应的决策值（x - y）是非零的。

Integrating DD and AR 集成 DD 和 AR

DD and AR are applied alternately to expand their joint deduction closure. The output of DD, which consists of new statements deduced with deductive rules, is fed into AR and vice versa. For example, if DD deduced ‘AB is parallel to CD’, the slopes of lines AB and CD will be updated to be equal variables in AR’s coefficient matrix A, defined in the ‘Algebraic reasoning’ section. Namely, a new row will be added to A with ‘1’ at the column corresponding to the variable slope(AB) and ‘−1’ at the column of slope(CD). Gaussian elimination and mixed-integer linear programming is run again as AR executes, producing new equalities as inputs to the next iteration of DD. This loop repeats until the joint deduction closure stops expanding. Both DD and AR are deterministic processes that only depend on the theorem premises, therefore they do not require any design choices in their implementation.
DD 和 AR 交替应用以扩展它们的联合推理闭包。DD 的输出，由推理规则推导出的新陈述，被输入到 AR 中，反之亦然。例如，如果 DD 推导出“AB 平行于 CD”，则在 AR 的系数矩阵 A 中，AB 和 CD 线的斜率将被更新为等变量，这在“代数推理”部分中有定义。即，A 中将添加一个新行，对应于变量斜率(AB)的列为‘1’，斜率(CD)的列为‘-1’。随着 AR 的执行，再次运行高斯消元和混合整数线性规划，产生新的等式作为 DD 下一次迭代的输入。这个循环重复，直到联合推理闭包停止扩展。DD 和 AR 都是确定性过程，仅依赖于定理前提，因此它们的实现不需要任何设计选择。

Proof pruning 证明剪枝

Although the set of immediate ancestors to any node is minimal, this does not guarantee that the fully traced back dependency subgraph G(N) and the necessary premise P are minimal. Here we define minimality to be the property that G(N) and P cannot be further pruned without losing conclusion reachability. Without minimality, we obtained many synthetic proofs with vacuous auxiliary constructions, having shallow relation to the actual proof and can be entirely discarded. To solve this, we perform exhaustive trial and error, discarding each subset of the auxiliary points and rerunning DD + AR on the smaller subset of premises to verify goal reachability. At the end, we return the minimum proof obtainable across all trials. This proof-pruning procedure is done both during synthetic data generation and after each successful proof search during test time.
尽管任何节点的直接祖先集合是最小的，这并不保证完全追溯的依赖子图 G(N) 和必要的前提 P 是最小的。这里我们定义最小性为 G(N) 和 P 不能进一步剪枝而不失去结论可达性的属性。在没有最小性的情况下，我们获得了许多具有空洞辅助构造的合成证明，与实际证明的关系浅薄，可以完全丢弃。为了解决这个问题，我们进行穷举试错，丢弃辅助点的每个子集，并在较小的前提子集上重新运行 DD + AR 以验证目标可达性。最后，我们返回在所有试验中可获得的最小证明。这种证明剪枝程序在合成数据生成期间和每次成功的证明搜索测试期间都会进行。

Parallelized data generation and deduplication
并行数据生成和去重

We run our synthetic-data-generation process on a large number of parallel CPU workers, each seeded with a different random seed to reduce duplications. After running this process on 100,000 CPU workers for 72 h, we obtained roughly 500 million synthetic proof examples. We reformat the proof statements to their canonical form (for example, sorting arguments of individual terms and sorting terms within the same proof step, etc.) to avoid shallow deduplication against itself and against the test set. At the end, we obtain 100 million unique theorem–proof examples. A total of 9 million examples involves at least one auxiliary construction. We find no IMO-AG-30 problems in the synthetic data. On the set of geometry problems collected in JGEX¹⁷, which consists mainly of problems with moderate difficulty and well-known theorems, we find nearly 20 problems in the synthetic data. This suggests that the training data covered a fair amount of common knowledge in geometry, but the space of more sophisticated theorems is still much larger.
我们在大量并行的 CPU 工作器上运行我们的合成数据生成过程，每个工作器都使用不同的随机种子以减少重复。在 72 小时内，使用 100,000 个 CPU 工作器运行此过程后，我们大约获得了 5 亿个合成证明示例。我们将证明语句重新格式化为它们的规范形式（例如，对单个术语的参数进行排序以及对同一证明步骤内的术语进行排序等），以避免对自身和对测试集的浅层去重。最终，我们获得了 1 亿个独特的定理-证明示例。总共有 900 万个示例涉及至少一个辅助构造。我们在合成数据中没有发现 IMO-AG-30 问题。在 JGEX ¹⁷ 收集的几何问题集上，这主要由难度适中和众所周知的定理组成，我们在合成数据中发现了近 20 个问题。这表明训练数据覆盖了几何学中相当数量的常识，但更复杂的定理空间仍然要大得多。

Language model architecture and training
语言模型架构和训练

We use the Meliad library³⁵ for transformer training with its base settings. The transformer has 12 layers, embedding dimension of 1,024, eight heads of attention and an inter-attention dense layer of dimension 4,096 with ReLU activation. Overall, the transformer has 151 million parameters, excluding embedding layers at its input and output heads. Our customized tokenizer is trained with ‘word’ mode using SentencePiece³⁶ and has a vocabulary size of 757. We limit the maximum context length to 1,024 tokens and use T5-style relative position embedding³⁷. Sequence packing^38,39 is also used because more than 90% of our sequences are under 200 in length. During training, a dropout⁴⁰ rate of 5% is applied pre-attention and post-dense. A 4 × 4 slice of TPUv3 (ref. ⁴¹) is used as its hardware accelerator. For pretraining, we train the transformer with a batch size of 16 per core and a cosine learning-rate schedule that decays from 0.01 to 0.001 in 10,000,000 steps. For fine-tuning, we maintain the final learning rate of 0.001 for another 1,000,000 steps. For the set-up with no pretraining, we decay the learning rate from 0.01 to 0.001 in 1,000,000 steps. We do not perform any hyperparameter tuning. These hyperparameter values are either selected to be a large round number (training steps) or are provided by default in the Meliad codebase.
我们使用 Meliad 库 ³⁵ 进行变压器训练，采用其基本设置。变压器具有 12 层，嵌入维度为 1,024，八个注意力头和一个维度为 4,096 的内部注意力密集层，激活函数为 ReLU。总的来说，变压器有 1.51 亿个参数，不包括其输入和输出头的嵌入层。我们的自定义分词器使用 SentencePiece ³⁶ 训练，采用‘词’模式，并且词汇量为 757。我们将最大上下文长度限制为 1,024 个令牌，并使用 T5 风格的相对位置嵌入 ³⁷ 。序列打包 ^38,39 也被使用，因为我们超过 90% 的序列长度在 200 以内。在训练期间，注意力前和密集后应用 5% 的丢弃率 ⁴⁰ 。作为硬件加速器，使用了 TPUv3 的 4 × 4 切片（参考 ⁴¹ ）。对于预训练，我们以每核 16 的批量大小训练变压器，并采用余弦学习率计划，从 0.01 降到 0.001，在 10,000,000 步骤中。对于微调，我们在另外 1,000,000 步骤中保持最终学习率为 0.001。对于没有预训练的设置，我们在 1,000,000 步骤中将学习率从 0.01 降到 0.001。我们不进行任何超参数调整。这些超参数值要么被选为一个大的整数（训练步骤），要么是 Meliad 代码库中的默认值。

Parallelized proof search
并行化证明搜索

Because the language model decoding process returns k different sequences describing k alternative auxiliary constructions, we perform a beam search over these k options, using the score of each beam as its value function. This set-up is highly parallelizable across beams, allowing substantial speed-up when there are parallel computational resources. In our experiments, we use a beam size of k = 512, the maximum number of iterations is 16 and the branching factor for each node, that is, the decoding batch size, is 32. This is the maximum inference-time batch size that can fit in the memory of a GPU V100 for our transformer size. Scaling up these factors to examine a larger fraction of the search space might improve AlphaGeometry results even further.
由于语言模型解码过程返回 k 个不同的序列，描述了 k 个替代辅助结构，我们对这些 k 个选项执行波束搜索，使用每个波束的得分作为其价值函数。这种设置在波束之间高度可并行化，当有并行计算资源时，允许大幅加速。在我们的实验中，我们使用的波束大小为 k = 512，最大迭代次数为 16，每个节点的分支因子，即解码批量大小为 32。这是我们的变压器大小可以适应 GPU V100 内存的最大推理时间批量大小。扩大这些因素以检查更大一部分搜索空间可能会进一步改善 AlphaGeometry 的结果。

For each problem, we used a pool of four GPU workers, each hosting a copy of the transformer language model to divide the work between alternative beams, and a pool of 10,000 CPU workers to host the symbolic solvers, shared across all beams across all 30 problems. This way, a problem that terminates early can contribute its share of computing power to longer-running problems. We record the running time of the symbolic solver on each individual problem, which—by design—stays roughly constant across all beams. We use this and the language model decoding speed to infer the necessary parallelism needed for each problem, in isolation, to stay under different time limits at the IMO in Extended Data Fig. 1.
对于每个问题，我们使用了四个 GPU 工作器的池，每个工作器都托管了一个变压器语言模型的副本，以在不同的波束之间分配工作，并使用了 10,000 个 CPU 工作器的池来托管符号求解器，跨所有 30 个问题的所有波束共享。这样，提前终止的问题可以将其计算能力的份额贡献给运行时间较长的问题。我们记录了符号求解器在每个单独问题上的运行时间，这通过设计在所有波束中大致保持恒定。我们使用这个和语言模型解码速度来推断每个问题单独需要的必要并行性，以保持在 IMO 的不同时间限制下，在扩展数据图 1 中。

The effect of data and search
数据和搜索的影响

We trained AlphaGeometry on smaller fractions of the original training data (20%, 40%, 60% and 80%) and found that, even at 20% of training data, AlphaGeometry still solves 21 problems, more than the strongest baseline (DD + AR + human-designed heuristics) with 18 problems solved, as shown in Extended Data Fig. 6a. To study the effect of beam search on top of the language model, we reduced the beam size and search depth separately during proof search and reported the results in Extended Data Fig. 6c,d. We find that, with a beam size of 8, that is, a 64 times reduction from the original beam size of 512, AlphaGeometry still solves 21 problems. A similar result of 21 problems can be obtained by reducing the search depth from 16 to only two, while keeping the beam size constant at 512.
我们在原始训练数据的较小比例（20%，40%，60%和 80%）上训练了 AlphaGeometry，并发现即使在训练数据的 20%时，AlphaGeometry 仍然解决了 21 个问题，比最强基线（DD + AR + 人为设计的启发式）多解决了 18 个问题，如扩展数据图 6a 所示。为了研究束搜索对语言模型的影响，我们在证明搜索过程中分别减小了束大小和搜索深度，并在扩展数据图 6c,d 中报告了结果。我们发现，当束大小为 8 时，即从原始束大小 512 减少 64 倍，AlphaGeometry 仍然解决了 21 个问题。通过将搜索深度从 16 减少到仅 2，同时保持束大小为 512 不变，也可以获得解决 21 个问题的类似结果。

Evaluation on a larger test set
在更大的测试集上的评估

We evaluated AlphaGeometry and other baselines on a larger test set of 231 geometry problems, curated in ref. ¹⁷. This set covers a wider range of sources outside IMO competitions: textbook examples and exercises, regional olympiads and famous geometry theorems; some are even more complex than typical IMO problems, such as the five circles theorem, Morley’s theorem or Sawayama and Thébault’s theorem. The results are reported in Extended Data Fig. 6b. The overall rankings of different approaches remained the same as in Table 1, with AlphaGeometry solving almost all problems (98.7%). The strongest baseline DD + AR + human-designed heuristics solves 92.2%, whereas the previous state of the art solves 75%.
我们在一个由 231 个几何问题组成的更大测试集上评估了 AlphaGeometry 和其他基线，这些问题在参考文献 ¹⁷ 中整理。这个集合涵盖了 IMO 竞赛之外更广泛的来源：教科书示例和练习、地区奥林匹克竞赛和著名的几何定理；有些问题甚至比典型的 IMO 问题更复杂，如五圆定理、莫雷定理或 Sawayama 和 Thébault 定理。结果在扩展数据图 6b 中报告。不同方法的总体排名与表 1 中的相同，AlphaGeometry 几乎解决了所有问题（98.7%）。最强基线 DD + AR + 人为设计的启发式解决了 92.2%，而之前的最先进技术解决了 75%。

AlphaGeometry framework and applicability to other domains
AlphaGeometry 框架及其适用性于其他领域

The strength of AlphaGeometry’s neuro-symbolic set-up lies in its ability to generate auxiliary constructions, which is an important ingredient across many mathematical domains. In Extended Data Table 3, we give examples in four other mathematical domains in which coming up with auxiliary constructions is key to the solution. In Extended Data Table 4, we give a line-by-line comparison of a geometry proof and an inequality proof for the IMO 1964 Problem 2, highlighting how they both fit into the same framework.
AlphaGeometry 的神经符号设置的强大之处在于其生成辅助构造的能力，这是许多数学领域中一个重要的组成部分。在扩展数据表 3 中，我们给出了四个其他数学领域中提出辅助构造是解决问题关键的例子。在扩展数据表 4 中，我们逐行比较了一份几何证明和一份不等式证明，用于 IMO 1964 问题 2，突出显示它们如何都适应同一框架。

Our paper shows that language models can learn to come up with auxiliary constructions from synthetic data, in which problem statements and auxiliary constructions are randomly generated together and then separated using the traceback algorithm to identify the dependency difference. Concretely, the AlphaGeometry framework requires the following ingredients:
我们的论文表明，语言模型可以学会从合成数据中提出辅助构造，其中问题陈述和辅助构造一起随机生成，然后使用回溯算法分开，以识别依赖差异。具体来说，AlphaGeometry 框架需要以下成分：

1. (1)

   An implementation of the domain’s objects and definitions.
   域对象和定义的实现。

2. (2)

   A random premise sampler.
   一个随机前提采样器。

3. (3)

   The symbolic engine(s) that operate within the implementation (1).
   在实现（1）中操作的符号引擎。

4. (4)

   A traceback procedure for the symbolic engine.
   符号引擎的回溯程序。

Using these four ingredients and the algorithm described in the main text, one can generate synthetic data for any target domain. As shown in our paper, there are non-trivial engineering challenges in building each ingredient. For example, current formalizations of combinatorics are very nascent, posing challenges to (1) and (2). Also, building powerful symbolic engines for different domains requires deep domain expertise, posing challenges to (3) and (4). We consider applying this framework to a wider scope as future work and look forward to further innovations that tackle these challenges.
使用这四种成分和主文中描述的算法，可以为任何目标领域生成合成数据。如我们的论文所示，构建每个成分存在非平凡的工程挑战。例如，组合学的当前形式化非常初期，给（1）和（2）带来挑战。此外，为不同领域构建强大的符号引擎需要深厚的领域专业知识，给（3）和（4）带来挑战。我们考虑将这个框架应用到更广泛的范围作为未来的工作，并期待进一步的创新来应对这些挑战。

Transformer in theorem proving
在定理证明中的变压器

Research in automated theorem proving has a long history dating back to the 1950s (refs. ^6,42,43), resulting in highly optimized first-order logic solvers such as E (ref. ⁴⁴) or Vampire⁴⁵. In the 2010s, deep learning matured as a new powerful tool for automated theorem proving, demonstrating great successes in premise selection and proof guidance^46,47,48,49, as well as SAT solving⁵⁰. On the other hand, transformer¹⁸ exhibits outstanding reasoning capabilities across a variety of tasks^51,52,53. The first success in applying transformer language models to theorem proving is GPT-f (ref. ¹⁵). Its follow up extensions^2,16 further developed this direction, allowing machines to solve some olympiad-level problems for the first time. Innovation in the proof-search algorithm and online training³ also improves transformer-based methods, solving a total of ten (adapted) IMO problems in algebra and number theory. These advances, however, are predicated on a substantial amount of human proof examples and standalone problem statements designed and curated by humans.
自动定理证明的研究有着悠久的历史，可以追溯到 1950 年代（参考文献 ^6,42,43 ），产生了如 E（参考文献 ⁴⁴ ）或 Vampire ⁴⁵ 这样的高度优化的一阶逻辑求解器。在 2010 年代，深度学习作为自动定理证明的一种新的强大工具成熟起来，在前提选择和证明指导 ^46,47,48,49 以及 SAT 求解 ⁵⁰ 中展示了巨大的成功。另一方面，变压器 ¹⁸ 在各种任务 ^51,52,53 中展示了出色的推理能力。将变压器语言模型应用于定理证明的第一个成功是 GPT-f（参考文献 ¹⁵ ）。其后续扩展 ^2,16 进一步发展了这一方向，使得机器首次能够解决一些奥林匹亚级别的问题。在证明搜索算法和在线训练 ³ 方面的创新也改进了基于变压器的方法，解决了总共十个（适应性的）IMO 问题，在代数和数论方面。然而，这些进步是基于大量人类证明示例和由人类设计和策划的独立问题声明的。

Geometry theorem proving 几何定理证明

Geometry theorem proving evolves in an entirely separate space. Its literature is divided into two branches, one of computer algebra methods and one of search methods. The former is largely considered solved since the introduction of Wu’s method²¹, which can theoretically decide the truth value of any geometrical statement of equality type, building on specialized algebraic tools introduced in earlier works^54,55. Even though computer algebra has strong theoretical guarantees, its performance can be limited in practice owing to their large time and space complexity⁵⁶. Further, the methodology of computer algebra is not of interest to AI research, which instead seeks to prove theorems using search methods, a more human-like and general-purpose process.
几何定理证明在一个完全独立的空间中发展。其文献分为两个分支，一个是计算机代数方法，另一个是搜索方法。自从吴方法 ²¹ 引入以来，前者在很大程度上被认为已经解决，理论上可以决定任何几何等式类型陈述的真值，这一方法建立在早期作品 ^54,55 中引入的专门代数工具之上。尽管计算机代数具有强大的理论保证，但由于其大的时间和空间复杂性 ⁵⁶ ，其性能在实践中可能受到限制。此外，计算机代数的方法论对人工智能研究不感兴趣，后者寻求使用搜索方法证明定理，这是一个更类似于人类且更通用的过程。

Search methods also started as early as the 1950s (refs. ^6,7) and continued to develop throughout the twentieth century^57,58,59,60. With the introduction of DD^10,17, area methods⁶¹ and full-angle methods³⁰, geometry solvers use higher-level deduction rules than Tarski’s or Hilbert’s axioms and are able to prove a larger number of more complex theorems than those operating in formal languages. Geometry theorem proving of today, however, is still relying on human-designed heuristics for auxiliary constructions^{10,11,12,13,14}. Geometry theorem proving falls behind the recent advances made by machine learning because its presence in formal mathematical libraries such as Lean³¹ or Isabelle⁶² is extremely limited.
搜索方法也早在 20 世纪 50 年代就开始了（参考文献 ^6,7 ）并在整个 20 世纪持续发展 ^57,58,59,60 。随着 DD ^10,17 、面积方法 ⁶¹ 和全角方法 ³⁰ 的引入，几何求解器使用比塔斯基或希尔伯特公理更高级别的演绎规则，能够证明比那些在形式语言中操作的定理更多、更复杂的定理。然而，当今的几何定理证明仍然依赖于人为设计的启发式方法进行辅助构造 ^{10,11,12,13,14} 。几何定理证明落后于机器学习最近取得的进展，因为它在如 Lean ³¹ 或 Isabelle ⁶² 等正式数学库中的存在极为有限。

Synthetic data in theorem proving
在定理证明中的合成数据

Synthetic data has long been recognized and used as an important ingredient in theorem proving^63,64,65,66. State-of-the-art machine learning methods make use of expert iteration to generate a curriculum of synthetic proofs^2,3,15. Their methods, however, only generate synthetic proofs for a fixed set of predefined problems, designed and selected by humans. Our method, on the other hand, generates both synthetic problems and proofs entirely from scratch. Aygun et al.⁶⁷ similarly generated synthetic proofs with hindsight experience replay⁶⁸, providing a smooth range of theorem difficulty to aid learning similar to our work. AlphaGeometry, however, is not trained on existing conjectures curated by humans and does not learn from proof attempts on the target theorems. Their approach is thus orthogonal and can be used to further improve AlphaGeometry. Most similar to our work is Firoiu et al.⁶⁹, whose method uses a forward proposer to generate synthetic data by depth-first exploration and trains a neural network purely on these synthetic data. Our work, on the other hand, uses breadth-first exploration, necessary to obtain the minimal proofs and premises, and uses a traceback algorithm to identify auxiliary constructions, thus introducing new symbols and hypotheses that the forward proposer cannot propose.
人工合成数据长期以来一直被认识到并用作定理证明中的一个重要成分 ^63,64,65,66 。最先进的机器学习方法利用专家迭代来生成合成证明的课程 ^2,3,15 。然而，他们的方法仅为一组固定的预定义问题生成合成证明，这些问题由人类设计和选择。另一方面，我们的方法从头开始生成合成问题和证明。Aygun 等人 ⁶⁷ 同样使用事后经验回放生成合成证明 ⁶⁸ ，提供了一个平滑的定理难度范围以帮助学习，类似于我们的工作。然而，AlphaGeometry 没有在人类策划的现有猜想上进行训练，也没有从目标定理的证明尝试中学习。因此，他们的方法是正交的，可以用来进一步改进 AlphaGeometry。与我们的工作最相似的是 Firoiu 等人 ⁶⁹ ，他们的方法使用前向提议者通过深度优先探索生成合成数据，并纯粹在这些合成数据上训练神经网络。另一方面，我们的工作使用广度优先探索，这是获得最小证明和前提所必需的，并使用回溯算法来识别辅助构造，从而引入前向提议者无法提出的新符号和假设。