【手撕LLM - Mixtral-8x7B】Pytorch 实现

原创课程➡️ 公众号：手撕LLM

137 人赞同了该文章

0. Preface

This article discusses the implementation of the mixture of experts in Mixtral 8x7B from a code perspective. It is recommended to read sMoE in advance

Little Winter Melon AIGC: 【Tearing Down LLM-sMoE】One Step Closer to GPT-4204 Likes · 11 CommentsArticle

1. Paper Overview

Mixtral of Experts mistral-AI

Mixtral-8x7B has sparked the technical direction of MoE, leading to the emergence of more MoE-optimized Trick. This article focuses on the model itself to provide an analysis:

Mixtral 8x7B adopts the sMoE model architecture. How are the details of the model? How is the routing load balancing calculated? How is the code implemented?
Mixtral 8x7B 的训练流程和推理流程是怎样的，如何提高训练和推理的效率？
Mixtral 8x7B 的 model parameters are calculated in what way?
Mixtral 8x7B performance rivals LLaMA2-70B and GPT-3.5, reaching top-tier standards, and in MBPP code capabilities surpass 3.5.

2. Mixtral 8x7B Model Architecture and Computational Flow

Mixtral is based on a transformer architecture [31] and uses the same modifications as described in [18], with the notable exceptions that Mixtral supports a fully dense context length of 32k tokens, and the feed forward blocks are replaced by Mixture-of-Expert layers (Section 2.1). The model architecture parameters are summarized in Table 1.

base的模型结构为Transformers的改版Mistral-7B The model structure of base is a modified version of Transformers, specifically Mistral-7B
MoE is applied to Feed Forward Blocks

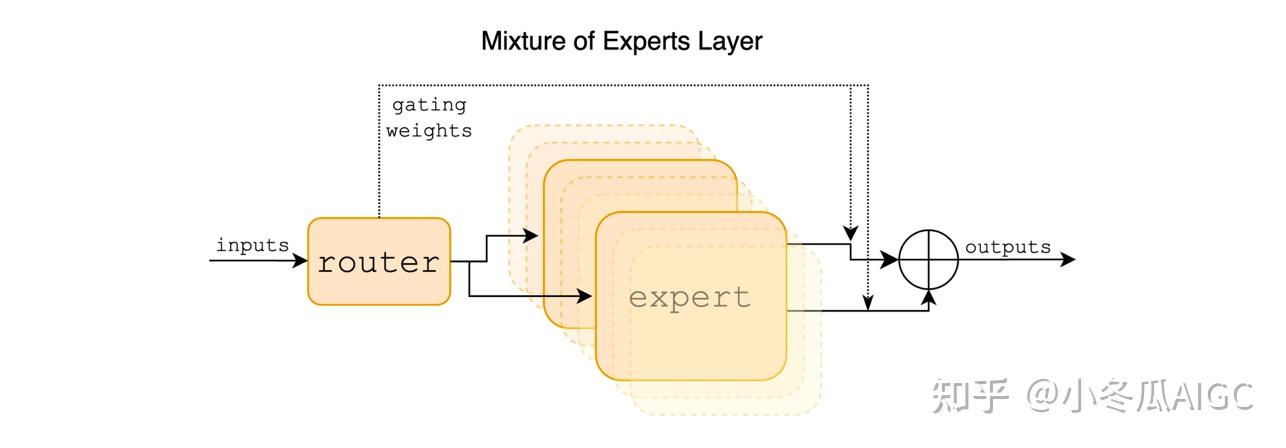
2.1 Model Architecture

In a Transformer model, the MoE layer is applied independently per token and replaces the feed-forward (FFN) sub-block of the transformer block. For Mixtral we use the same SwiGLU architecture as the expert function Ei(x) and set K = 2. This means each token is routed to two SwiGLU sub-blocks with different sets of weights. Taking this all together, the output y for an input token x is computed as:

$y = \sum_{i = 0}^{n - 1} Softmax (Top2 (x \cdot W_{g}))_{i} \cdot {SwiGLU}_{i} (x)$ y=\sum^{n-1}_{i=0}\text{Softmax}(\text{Top2}(x \cdot W_g))_i \cdot \text{SwiGLU}_i(x)

For LLaMA2 or Mistral-7B, their MLP is in the form of SwiGLU
In Mixtral-8x7B, the Decoder layer of each layer replaces the MLP with sMoE

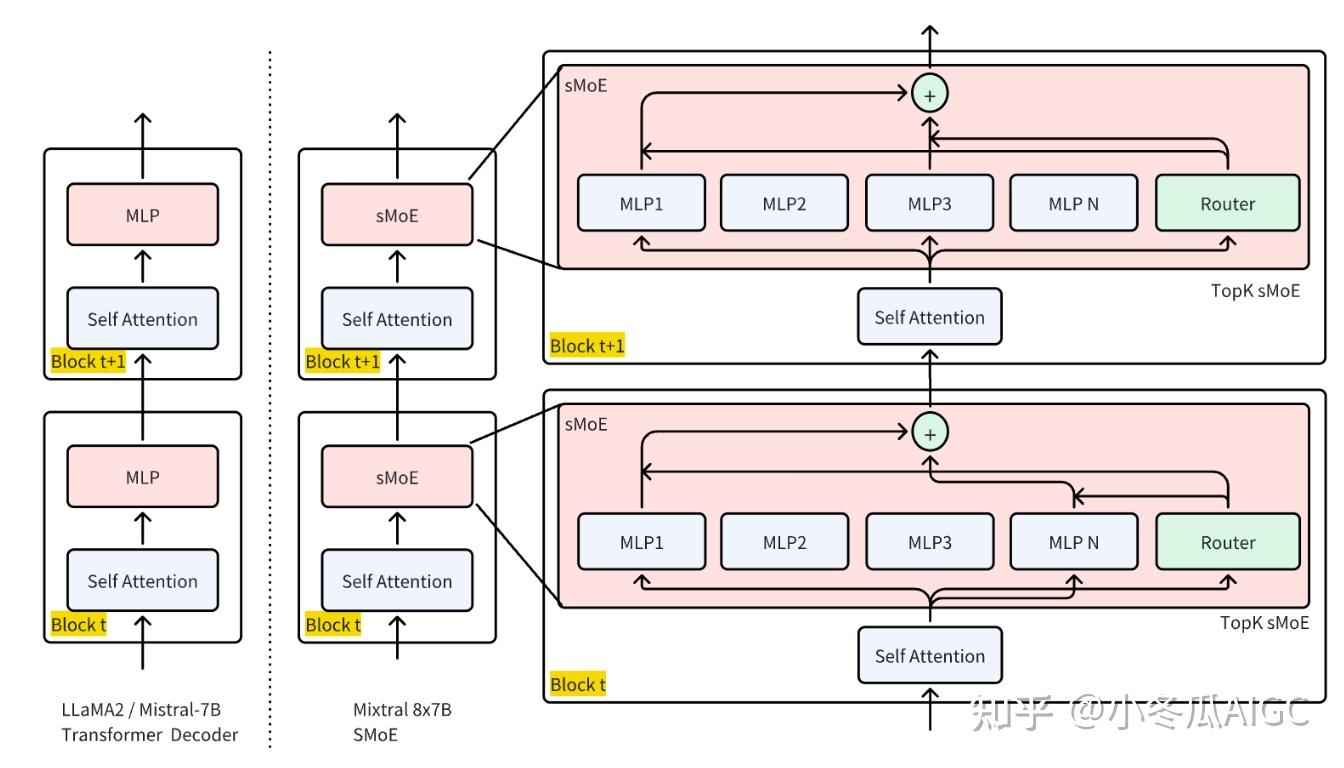
Transformers Mixtral-of-Expert 代码实现:

In the Huggingface Transformers framework, Mixtral mainly consists of two parts

MixtralDecoderLayer
MixtralSparseMoeBlock：Replace the original MLP layer

from transformers import AutoModelForCausalLM, AutoTokenizer, AutoConfig
import torch
import torch.nn.functional as F

model_id = "mistralai/Mixtral-8x7B-Instruct-v0.1"

# 创建小模型用于调试
config = AutoConfig.from_pretrained(model_id)
config.num_hidden_layers = 2
config.num_attention_heads = 8
config.hidden_size = 128
config.intermediate_size = 256
config.intermediate_size = config.hidden_size*2
config.num_experts_per_tok = 2 # Top-2 专家数量
config.num_local_experts = 8   # 专家总数量
# print(config)

model =  AutoModelForCausalLM.from_config(config)
print(model)

Output result

MixtralForCausalLM(
  (model): MixtralModel(
    (embed_tokens): Embedding(32000, 128)
    (layers): ModuleList(
      (1): MixtralDecoderLayer(
        (self_attn): MixtralAttention(
          (q_proj): Linear(in_features=128, out_features=128, bias=False)
          (k_proj): Linear(in_features=128, out_features=128, bias=False)
          (v_proj): Linear(in_features=128, out_features=128, bias=False)
          (o_proj): Linear(in_features=128, out_features=128, bias=False)
          (rotary_emb): MixtralRotaryEmbedding()
        )
        (block_sparse_moe): MixtralSparseMoeBlock(
          (gate): Linear(in_features=128, out_features=8, bias=False)
          (experts): ModuleList(
            (0-7): 8 x MixtralBLockSparseTop2MLP(
              (w1): Linear(in_features=128, out_features=256, bias=False)
              (w2): Linear(in_features=256, out_features=128, bias=False)
              (w3): Linear(in_features=128, out_features=256, bias=False)
              (act_fn): SiLU()
            )
          )
        )
        (input_layernorm): MixtralRMSNorm()
        (post_attention_layernorm): MixtralRMSNorm()
      )
    )
    (norm): MixtralRMSNorm()
  )

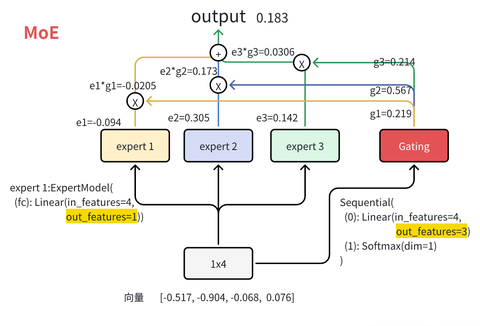
2.2 SMoE Layer Implementation
2.2.1 Single Expert Implementation

import torch
from torch import nn
from transformers import MixtralConfig

class MixtralBLockSparseTop2MLP(nn.Module):
    def __init__(self, config: MixtralConfig):
        super().__init__()
        self.ffn_dim = config.intermediate_size
        self.hidden_dim = config.hidden_size

        self.w1 = nn.Linear(self.hidden_dim, self.ffn_dim, bias=False)
        self.w2 = nn.Linear(self.ffn_dim, self.hidden_dim, bias=False)
        self.w3 = nn.Linear(self.hidden_dim, self.ffn_dim, bias=False)

        self.act_fn = nn.SiLU()

    # Forward 是 SwiGLU
    def forward(self, hidden_states): 
        y = self.act_fn(self.w1(hidden_states)) * self.w3(hidden_states)
        y = self.w2(y)
        return y

x = torch.randn(1, 64, 128)
expert = MixtralBLockSparseTop2MLP(config)
print('单个专家为原LLaMA的MLP层')
print(expert)
g = expert(x)
print('单个专家输入:', x.shape)
print('单个专家输出结果：', g.shape)

Result

单个专家为原LLaMA的MLP层
MixtralBLockSparseTop2MLP(
  (w1): Linear(in_features=128, out_features=256, bias=False)
  (w2): Linear(in_features=256, out_features=128, bias=False)
  (w3): Linear(in_features=128, out_features=256, bias=False)
  (act_fn): SiLU()
)
单个专家输入:
torch.Size([1, 64, 128])
单个专家输出结果：
torch.Size([1, 64, 128])

2.2.2 Hybrid Expert Implementation

class MixtralSparseMoeBlock(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.hidden_dim = config.hidden_size
        self.ffn_dim = config.intermediate_size
        self.num_experts = config.num_local_experts
        self.top_k = config.num_experts_per_tok

        # gating
        self.gate = nn.Linear(self.hidden_dim, self.num_experts, bias=False)

        # 多个 SwiGLU MLP 层组成混合专家
        self.experts = nn.ModuleList([MixtralBLockSparseTop2MLP(config) \
                                      for _ in range(self.num_experts)])

x = torch.randn(1, 64, 128)
experts = MixtralSparseMoeBlock(config)
print('多个专家混合专家')
print(experts)

Result:

多个专家混合专家
MixtralSparseMoeBlock(
  (gate): Linear(in_features=128, out_features=8, bias=False)
  (experts): ModuleList(
    (0-7): 8 x MixtralBLockSparseTop2MLP(
      (w1): Linear(in_features=128, out_features=256, bias=False)
      (w2): Linear(in_features=256, out_features=128, bias=False)
      (w3): Linear(in_features=128, out_features=256, bias=False)
      (act_fn): SiLU()
    )
  )
)

In the above, we have implemented the key structure of the model, but the sMoE Forward has not been implemented

2.3 SMoE Calculation Process

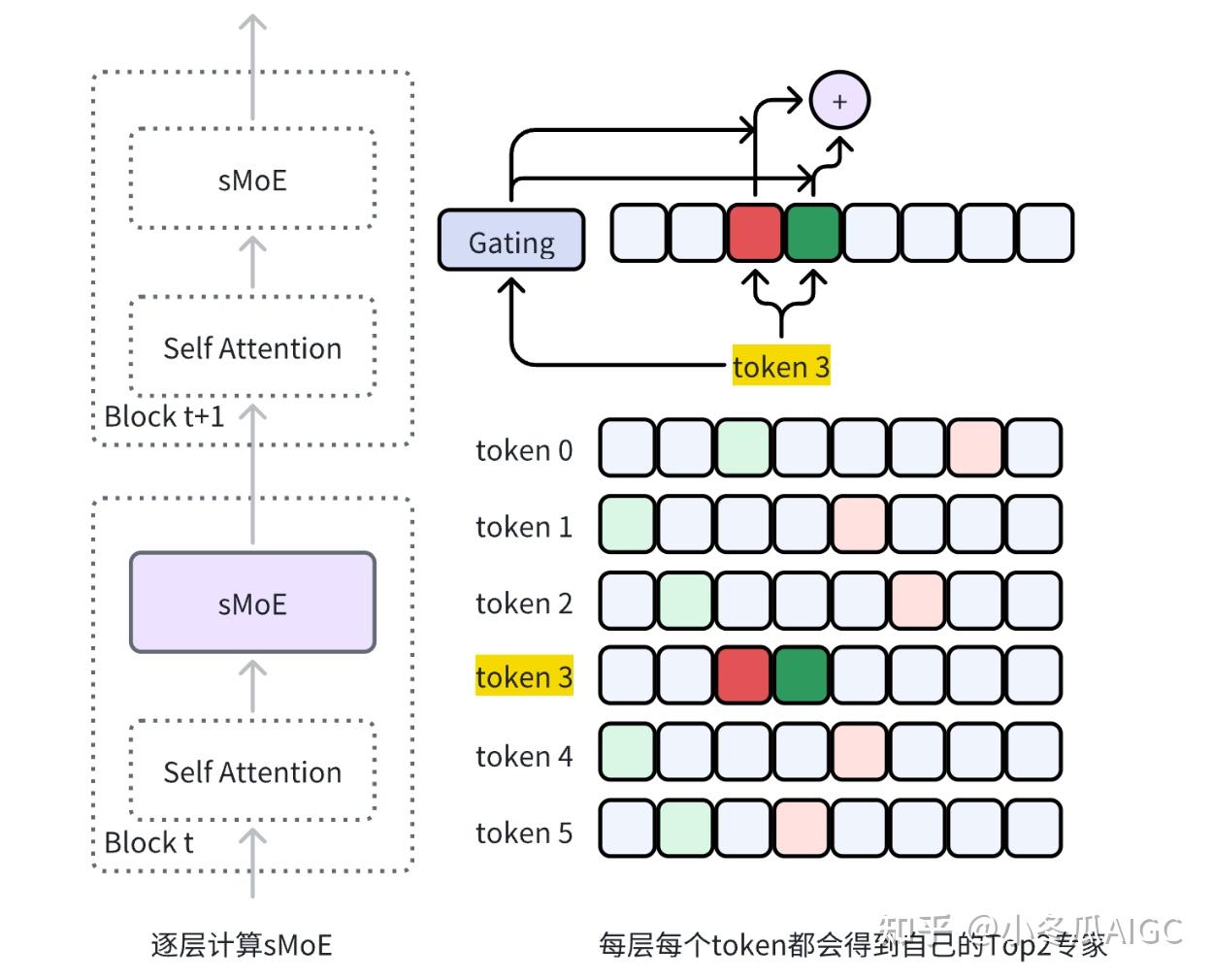
2.3.1 Gating process

The following represents the computation process for multiple token gating

# 阶段一
# 计算稀疏 gating 值
tokens = 6
x = torch.randn(1, tokens, 128) # 6个token
hidden_states = x
batch_size, sequence_length, hidden_dim = hidden_states.shape
hidden_states = hidden_states.view(-1, hidden_dim)

 # 每层都会产生router_logits, 将用于最后作 load balance loss
router_logits = experts.gate(hidden_states)
print(f'experts.gate output router logits : \n {router_logits}')

# 计算 TopK 的 专家 logits 和 Top2 专家的位置
routing_weights = F.softmax(router_logits, dim=1, dtype=torch.float)
print(f'softmax weight  : \n {routing_weights}')

routing_weights, selected_experts = torch.topk(routing_weights, \
                                               experts.top_k, dim=-1)
print(f'expert select : \n {selected_experts}')
print(f'topk : \n {routing_weights}')

routing_weights /= routing_weights.sum(dim=-1, keepdim=True)
print(f'topk归一化 : \n {routing_weights}')

routing_weights = routing_weights.to(hidden_states.dtype)

## One Hot 编码
expert_mask = torch.nn.functional.one_hot(selected_experts, \
                                          num_classes=experts.num_experts).permute(2, 1, 0)
for i in range(tokens):
    print(f'【token_{i}】\n', expert_mask[:,:,i])

追踪x3的结果

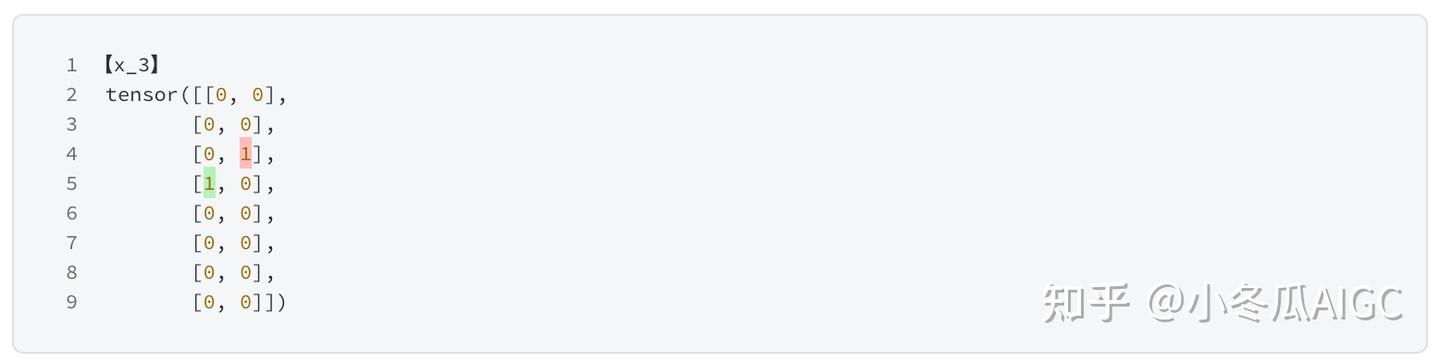
2.3.2 Expert process

$y = \sum_{i = 0}^{n - 1} Softmax (Top2 (x \cdot W_{g}))_{i} \cdot {SwiGLU}_{i} (x)$ y = \sum ^{n-1}_{i=0}\text{Softmax}(\text{Top2}(x\cdot W_g))_i \cdot \text{SwiGLU}_i(x)

sMoE is based on selecting token for computation
token Pre-order: The left figure selects token3 for expert 2 and expert 3 to compute the sMoE result
expert Pre-order: The result of sMoE is obtained by sequentially calculating expert2 and expert3 to get token3

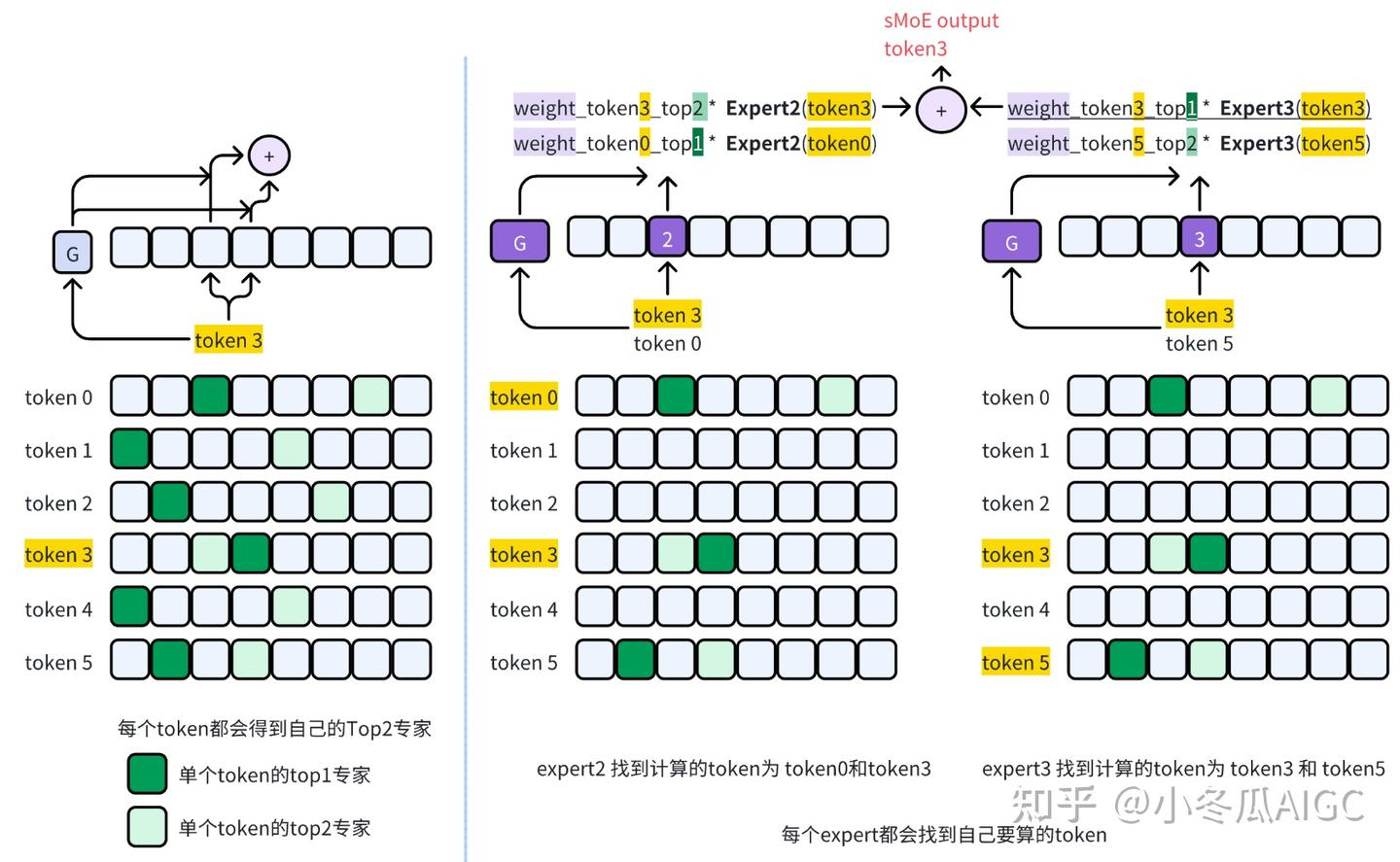
The implementation result of the code is:

## 最终结果
final_hidden_states = torch.zeros(
    (batch_size * sequence_length, hidden_dim), \
        dtype=hidden_states.dtype, device=hidden_states.device
)
print(f'final moe result shape for each token: {final_hidden_states.shape}')

# 每个专家收集需要计算token
for expert_idx in range(experts.num_experts):

    print(f'--------expert {expert_idx} ---------')

    expert_layer = experts.experts[expert_idx]
    print(expert_mask[expert_idx])
    idx, top_x = torch.where(expert_mask[expert_idx])
    print(f'专家 {expert_idx} 计算的样本编号:',top_x.tolist()) # select x_idx for expert top1
    print(f'专家 {expert_idx} top1:0, top2:1 ',idx.tolist()) # 0 is top1 ,1 is top2
    print(f'有 {len(top_x)} / {x.shape[1]} token 选到专家 {expert_idx}')
    
    top_x_list = top_x.tolist()
    idx_list = idx.tolist()

    current_state = hidden_states[None, top_x_list].reshape(-1, hidden_dim)

    # expert_0(x) * routing_weights
    current_hidden_states = expert_layer(current_state)  \
                            * routing_weights[top_x_list, idx_list, None]

    # 将计算的单个专家结果填入到结果表里
    final_hidden_states.index_add_(0, top_x, current_hidden_states.to(hidden_states.dtype))

    print(current_state.shape) 
    print(routing_weights[top_x_list, idx_list, None].shape)
    print(current_hidden_states.shape)
    print(final_hidden_states.shape)

    # if expert_idx == 1: break

The output result is

2.4 Router Load Balence 计算

The implementation of routing load balancing comes from Switch Transformers

Computes auxiliary load balancing loss as in Switch Transformer - implemented in Pytorch. See Switch Transformer for more details. This function implements the loss function presented in equations (4) - (6) of the paper. It aims at penalizing cases where the routing between experts is too unbalanced.

2.4.1 Switch Transformers Load Balance Loss

This algorithm is a simplified version of sMoE, removing the original estimation of balance loss calculation in load balance balance

$l o s s = α \cdot N \cdot \sum_{i = 1}^{N} f_{i} \cdot P_{i}$ loss = \alpha\cdot N\cdot \sum ^N_{i=1}f_i\cdot P_i

$f_{i} = \frac{1}{T} \sum_{x \in B} 1 {argmax p (x) = i}$ f_i = \frac{1}{T}\sum_{x\in\mathcal{B}}\mathbb{1}\{\text{argmax }p(x)=i\}

fi: the probability of the number of tokens assigned to the i-th expert in a batch

$P_{i} = \frac{1}{T} \sum_{x \in B} p_{i} (x)$ P_i=\frac{1}{T}\sum_{x\in \mathcal{B}}p_i(x)

Pi: In a batch of T tokens, the probability of each expert selecting the tokens and

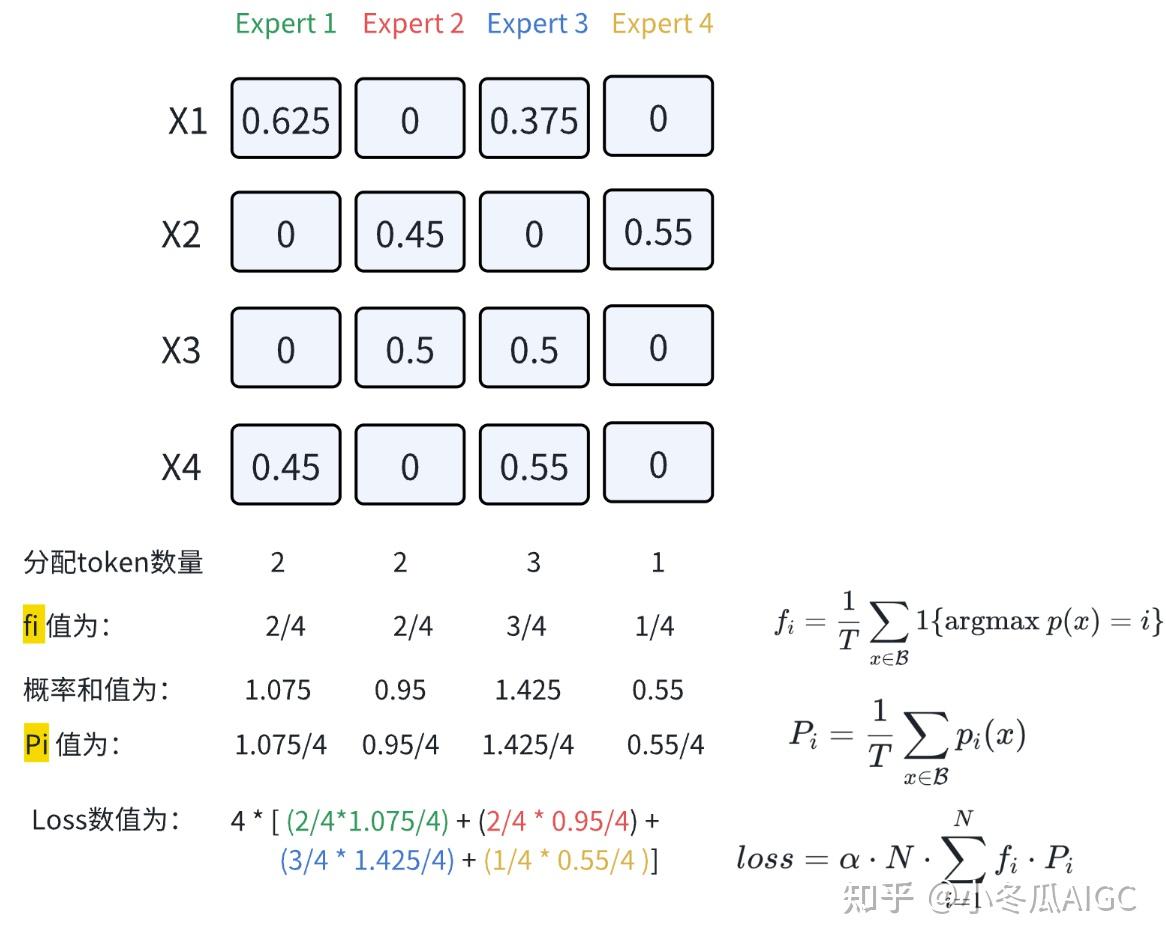
2.4.2 Mixtral Load Balance Loss Calculation Process

You can imagine that layer norm is just applied to all tokens within the current layer, while load balancing is handled over a broader scope, calculating the single expert load for all tokens across all layers, and summing these values to obtain the overall load balancing loss for the network

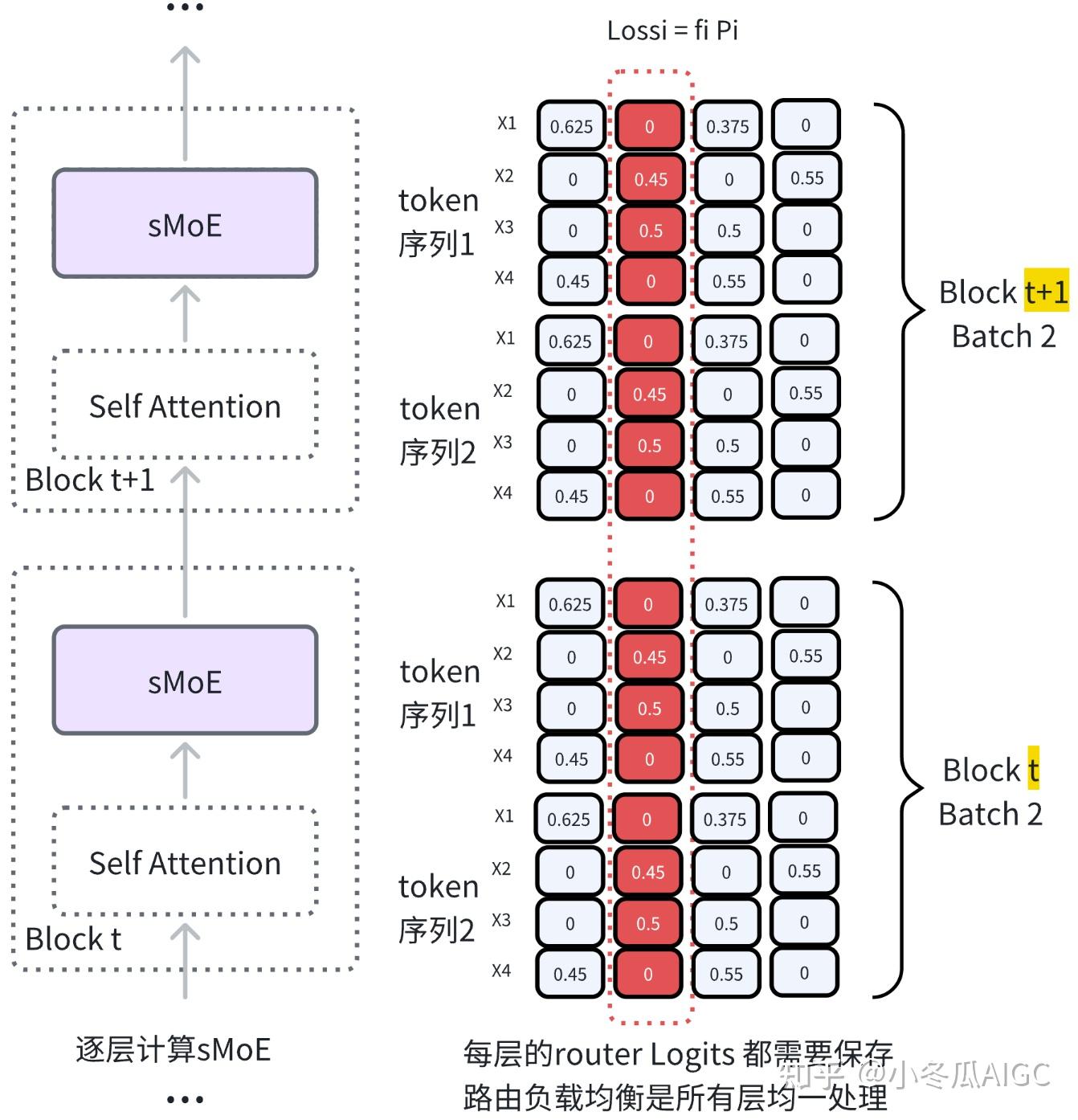
2.4.3 Manual Load Balancing

import torch

num_experts = 8
batch = 10 
seq_length = 6
top_k = 2

print(f'sMoE num_experts:{num_experts} top_k:{top_k} batch:{batch} seq_length:{seq_length}')

router_logits_1 = torch.randn(batch, seq_length, num_experts).view(-1,num_experts) # layer 1
router_logits_2 = torch.randn(batch, seq_length, num_experts).view(-1,num_experts) # layer 2
router_logits = [router_logits_1, router_logits_2] 

concatenated_gate_logits = torch.cat(router_logits, dim = 0)
print('单层gating的路由logits:', router_logits_1.shape) 
print('两层gating的路由logits:', concatenated_gate_logits.shape)

print('根据logits top-k 计算热独编码')
routing_weights = torch.nn.functional.softmax(concatenated_gate_logits, dim=-1)
_, selected_experts = torch.topk(routing_weights, top_k, dim=-1)
expert_mask = torch.nn.functional.one_hot(selected_experts, num_experts)
print(expert_mask.shape)

tokens_sum_expert = torch.sum(expert_mask.float(), dim=0)
tokens_per_expert = torch.mean(expert_mask.float(), dim=0)
print(f'top1 每个专家平均处理的token   :', tokens_sum_expert[0])
print(f'top2 每个专家平均处理的token fi:', tokens_per_expert[1])
print(f'top1与top2水平合计', tokens_per_expert.sum(dim=1))

# Compute the average probability of routing to these experts
router_prob_per_expert = torch.mean(routing_weights, dim=0)
print('router_prob_per_expert Pi: ' , router_prob_per_expert)

print( '每个专家的负载：',  tokens_per_expert * router_prob_per_expert.unsqueeze(0))
overall_loss = torch.sum(tokens_per_expert * router_prob_per_expert.unsqueeze(0))
print('final loss:', overall_loss)

The settlement result is:

sMoE num_experts:8 top_k:2 batch:10 seq_length:6
单层gating的路由logits:
torch.Size([60, 8])
两层gating的路由logits:
torch.Size([120, 8])
根据logits top-k 计算热独编码
torch.Size([120, 2, 8])
top1 每个专家平均处理的token   : tensor([10., 14., 19., 17., 14.,  9., 17., 20.])
top2 每个专家平均处理的token fi: tensor([0.1667, 0.1333, 0.1833, 0.0833, 0.1167, 0.1500, 0.0667, 0.1000])
top1与top2水平合计 tensor([1., 1.])
router_prob_per_expert Pi:  tensor([0.1236, 0.1184, 0.1351, 0.1168, 0.1311, 0.1147, 0.1156, 0.1447])
每个专家的负载： tensor([[0.0103, 0.0138, 0.0214, 0.0165, 0.0153, 0.0086, 0.0164, 0.0241],
        [0.0206, 0.0158, 0.0248, 0.0097, 0.0153, 0.0172, 0.0077, 0.0145]])
final loss: tensor(0.2520)

The gating logits are cross-batch and cross-layer, acting on each token in every layer

3. Mixtral 8x7B parameter calculation

3.1 Original paper description

The 13B refers to the number of model parameters involved in a single token. During actual inference, each token has different experts, so the actual operation still runs with 47B parameters. Using sMoE does not reduce the memory usage.

3.2 Model parameter calculation

Ignore GQA calculation

dim = 4096
n_layers = 32
head_dim = 128
hidden_dim = 14336
n_heads = 32
n_kv_heads = 8 # ignore GQA
vocab_size = 32000
num_experts = 8
top_k_experts = 2

# attention mlp layernorm
llama_num = n_layers * (dim * dim * 4 + hidden_dim * dim * 3 + 2 * dim ) \
        + 2 * vocab_size * dim 
print('llama:', llama_num)

# attention 【mlp*8】 layernorm
moe_num = n_layers * (dim * dim * 4 + hidden_dim * dim * 3 * 8 + 2 * dim ) \
        + 2 * vocab_size * dim 
print('moe:', moe_num)

# attention 【mlp*2】 layernorm
# ToP2-inference
moe_num = n_layers * (dim * dim * 4 + hidden_dim * dim * 3 * 2 + 2 * dim ) \
        + 2 * vocab_size * dim 
print('moe top2:', moe_num)

Parameter results

llama: 8047034368
moe: 47507046400
moe inference: 13684178944

4. MoE extension

4.1 MegaBlocks

MoE layers can be run efficiently on single GPUs with high performance specialized kernels. For example, Megablocks

MegaBlocks implements sparse MoE computation

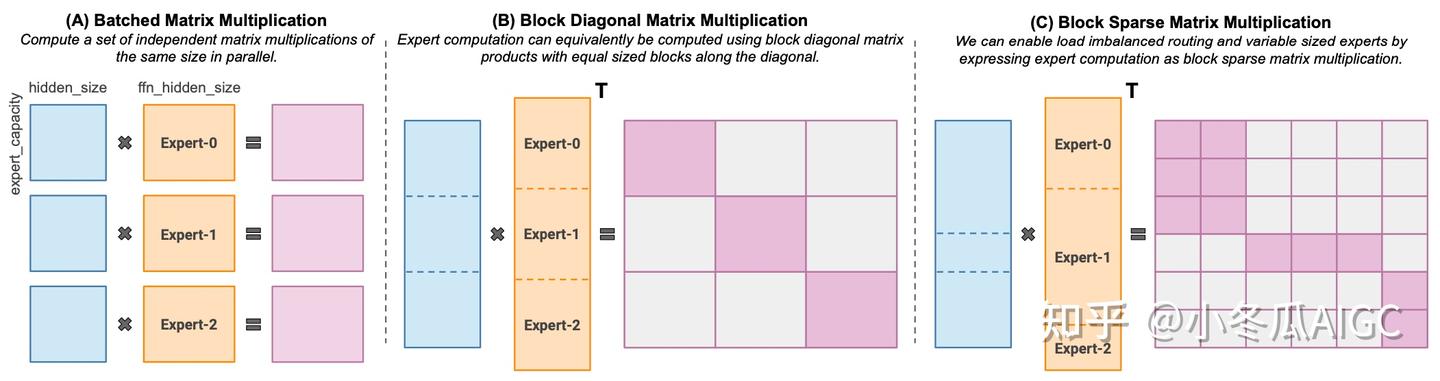
By the way, XFormers also implements operators with similar ideas, where batch attention is achieved through Mask to realize sparse computation across multiple sequences.

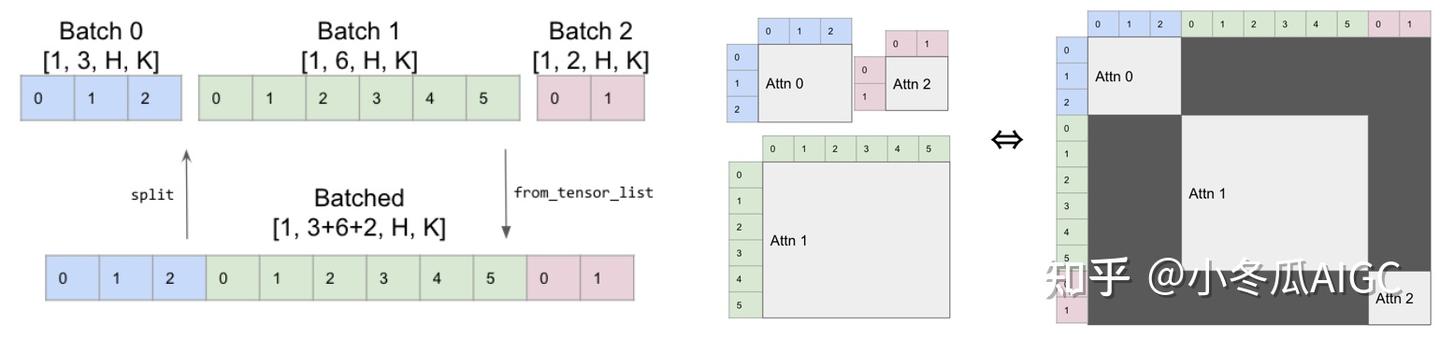
4.2 GShard

Mixtral is mentioned in the paper under load balance, referring to GShard, the first work to introduce MoE into Transformers

This formulation is similar to the GShard architecture [21], with the exceptions that we replace all FFN sub-blocks by MoE layers while GShard replaces every other block, and that GShard uses a more elaborate gating strategy for the second expert assigned to each token.

GShard allocates different experts on different GPUs, while other parameters are shared. Data is dispatched to the experts, and the aggregation of expert results is achieved by the All-to-All operator

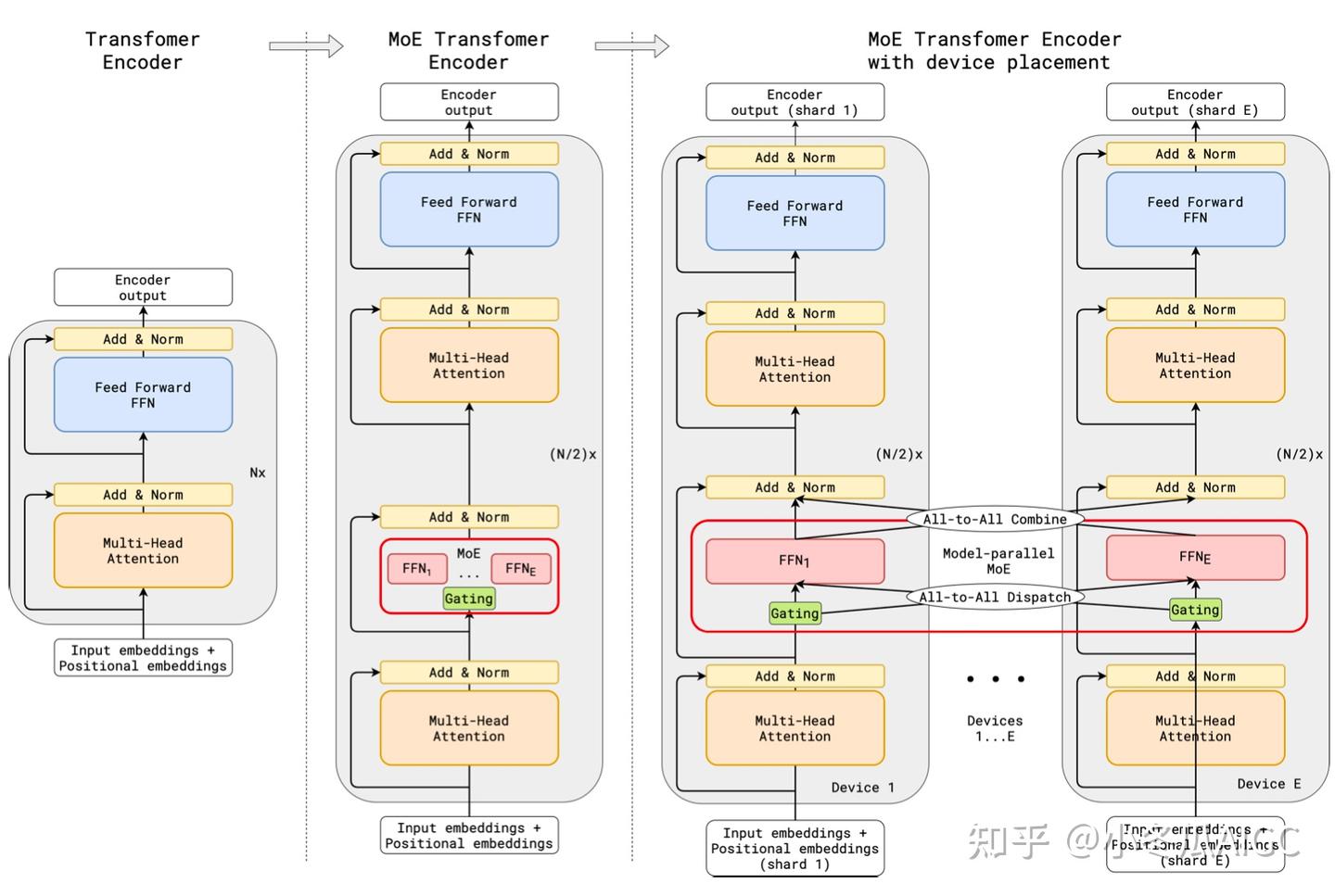
DeepSpeed-MoE source code implements All-to-All as follows

class _AllToAll(torch.autograd.Function):

    @staticmethod
    def forward(
            ctx: Any,
            # TODO: replace with DS process group
            group: torch.distributed.ProcessGroup,
            input: Tensor) -> Tensor:  # type: ignore
        ctx.group = group
        input = input.contiguous()
        output = torch.empty_like(input)
        dist.all_to_all_single(output, input, group=group)
        return output

    @staticmethod
    def backward(ctx: Any, *grad_output: Tensor) -> Tuple[None, Tensor]:
        return (None, _AllToAll.apply(ctx.group, *grad_output))
        
class MOELayer(Base):
     # ...
     def forward(self, *input: Tensor, **kwargs: Any) -> Tensor:
        # ...
        dispatched_input = _AllToAll.apply(self.ep_group, dispatched_input)

        # Re-shape after all-to-all: ecm -> gecm
        dispatched_input = dispatched_input.reshape(self.ep_size, self.num_local_experts, -1, d_model)

        expert_output = self.experts(dispatched_input)

        expert_output = _AllToAll.apply(self.ep_group, expert_output)

    #...

4.3 DeepSpeed-MoE

A more engineering-oriented implementation can be seen in the open-source solution of DeepSpeed-MoE
MoE layer uses Expert-Parallelism for parallelism, and AlltoAll is implemented as described above
Non-MoE layers use TP+DP

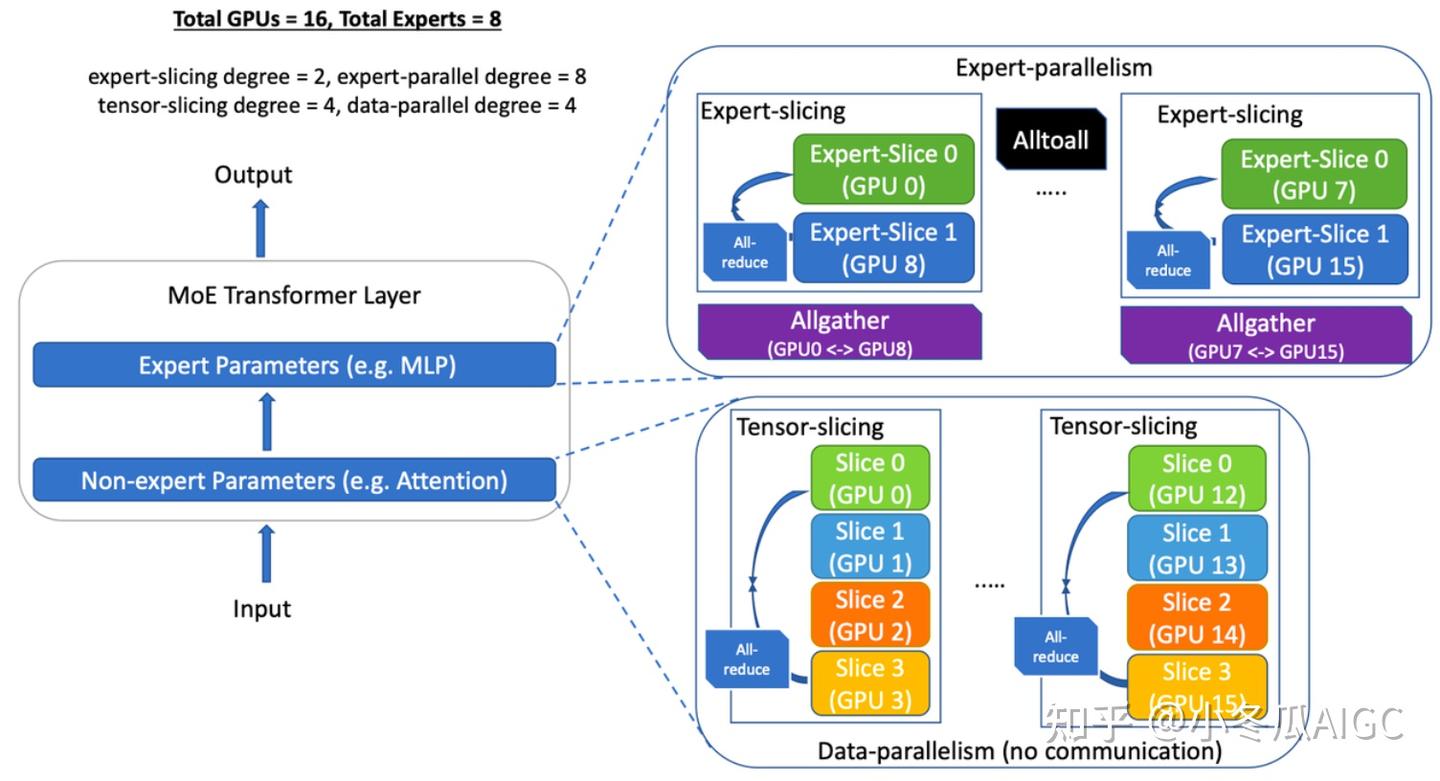
4.4 LLaMA-MoE

Mixtral 8x7B can't be trained? Try converting the original MLP in LLaMA to LLaMA-MoE

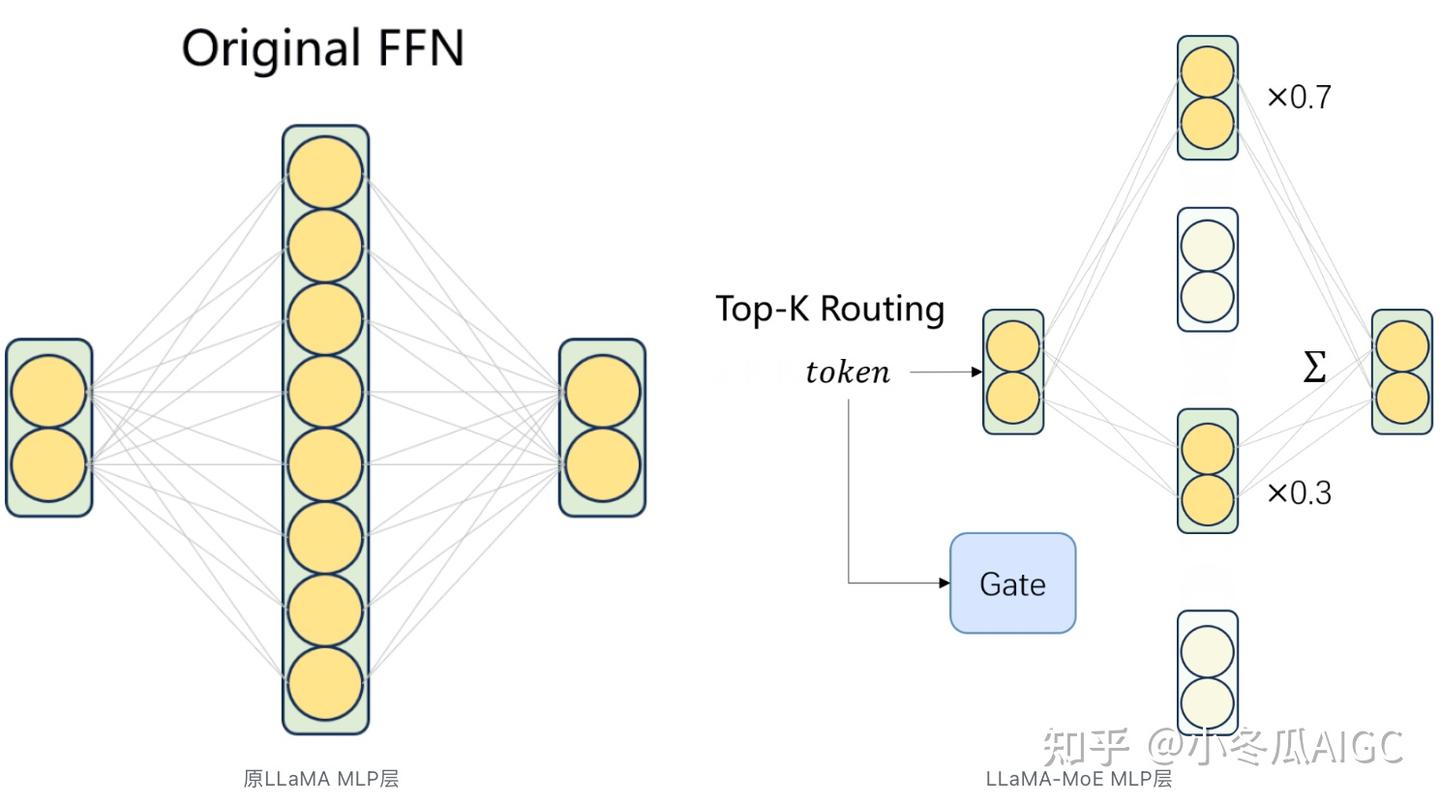
LLaMA-MoE the key code involves replacing the SwiGLU layer in the original LLaMA with LinearGLUExperts

 class LinearGLUExperts(nn.Module):
    # ...
    def __init__(...):
        # ... 
        # 每个专家都创建SwiGLU MLP层
        for i in range(num_experts):
            # this matrix will be transposed when performing linear forwarding
            this_expert_weight_gate = nn.Parameter(
                torch.empty((size_experts[i], in_features), **factory_kwargs)
            )
            # this matrix will be transposed when performing linear forwarding
            this_expert_weight_up = nn.Parameter(
                torch.empty((size_experts[i], in_features), **factory_kwargs)
            )
            # this matrix will be transposed when performing linear forwarding
            this_expert_weight_down = nn.Parameter(
                torch.empty((out_features, size_experts[i]), **factory_kwargs)
            )
            self.weight_gate.append(this_expert_weight_gate)
            self.weight_up.append(this_expert_weight_up)
            self.weight_down.append(this_expert_weight_down)
        # ...

5. Mixtral 8x7B Summary & Further Reading

Mixtral 8x7B implementation is not complicated, where the load-balance loss is calculated on the expert-wise dimension
The currently released model still focuses on the model architecture, looking forward to mistral.AI launching innovative alignment solutions.
Distributed training involving multiple machines and multiple cards for sMoE requires significant engineering skills. Different model architectures and clusters can have various DP\TP\EP... combination schemes. Besides, this series recommends DeepSpeed.

In Mixtral, for the counterintuitive argument in the experiment, the expert's knowledge operates at the token level, rather than the domain level. If you are interested in MoE, you can further analyze it

Meng Fanxu: Mixtral-8x7B model digging a hole

Reference

Fang Jiarui: Interpretation of MoE Training Paper - Megablocks: Breaking the Dynamic Routing Limitations

Ximen Yushao: Distributed Acceleration for Training and Inference of MoE Large Models — A Quick Read of the DeepSpeed-MoE Paper

Eating jelly without spitting out the jelly skin: Large Model Distributed Training Parallel Technology (Part 8) - MOE Parallel
Meng Fanxu: Mixtral-8x7B model digging a hole
Mixtral-of-experts
Mistral-7B
Gshard
Switch Transformers
sMoE
Transformers-Mixtral-of-Experts
DeepSpeed-MoE
Megablocks
LLaMA-MoE

Hand-Tearing RLHF explains how to systematically perform LLM alignment engineering

Xiaodonggua AIGC: [Tearing Apart RLHF_Weak-to-Strong] New Super Alignment Ideas from OpenAI (Including Code Analysis)

Little Winter Melon AIGC: [Tearing Apart Safe RLHF] PPO Dancing with Shackles on Its Feet

Xiaodonggua AIGC: [Tearing Apart RLHF-Rejection Sampling] How to Gracefully Transition from SFT to PPO

Little Winter Melon AIGC: [Tearing Apart RLHF-LLaMA2] Reward Model PyTorch Implementation

《Tearing Apart LLM》 series of articles + original courses: LLM principles covering Pretrained/PEFT/RLHF/high-performance computing

Little Winter Melon AIGC: 【Tearing Down LLM-sMoE】One Step Closer to GPT-4204 Likes · 11 CommentsArticle

Little Winter Melon AIGC: [Tearing down LLM-Speculative Decoding] Large Models Enter the "Parallel" Decoding Era

Xiaodonggua AIGC: 【Tearing down LLM-FlashAttention2】Just because the For loop optimization is too beautiful

Little Winter Melon AIGC: 【Tearing Apart LLM-FlashAttention】Starting from softmax, an ultra-long, beginner-friendly article!!

Little Winter Melon AIGC: 【Tearing Down LLM-Generation】Top-K + Repetition Penalty

Little Winter Melon AIGC: 【Tearing Down LLM-KVCache】The Past and Present of the Memory Bandit--Code Included at the End of the Article

Little Winter Melon AIGC: [Tearing apart LLM-QLoRA] NF4 and Double Quantization - Source Code Analysis

Little Winter Melon AIGC: 【Tearing apart LLM-RWKV】Reconstructing RNN Efficiency Surpasses Transformer

"Tearing Apart Agent" explores Agent methods that could lead to AGI from a code and engineering perspective

Little Winter Melon AIGC: 【Tearing Apart Agent-ReAct】Think Clearly Before Acting, Reduce LLM Hallucinations

I am Xiaodonggua AIGC, sharing original long-form articles with knowledge that has helped many students quickly achieve their goals

LLM track Research directions: LLM, RLHF, Safety, Alignment

Edited on 2024-03-08 17:33・IP location Beijing

Content belongs to the column

Hand tear LLM

LLM, RLHF, Safety

Master the large model technology

Collect high-quality articles on large model technology~

"Sincere appreciation, hands leave fragrance"

No one has appreciated it yet, come and be the first to appreciate it!

LLM

MOE

Large model

【手撕LLM - Mixtral-8x7B】Pytorch 实现

0. Preface

1. Paper Overview

2. Mixtral 8x7B Model Architecture and Computational Flow

2.1 Model Architecture

2.2 SMoE Layer Implementation
2.2.1 Single Expert Implementation

2.2.2 Hybrid Expert Implementation

2.3 SMoE Calculation Process

2.3.1 Gating process

2.3.2 Expert process

2.4 Router Load Balence 计算

2.4.1 Switch Transformers Load Balance Loss

2.4.2 Mixtral Load Balance Loss Calculation Process

2.4.3 Manual Load Balancing

3. Mixtral 8x7B parameter calculation

3.1 Original paper description

3.2 Model parameter calculation

4. MoE extension

4.1 MegaBlocks

4.2 GShard

4.3 DeepSpeed-MoE

4.4 LLaMA-MoE

5. Mixtral 8x7B Summary & Further Reading

Reference

Content belongs to the column

Hand tear LLM

Master the large model technology

Recommended reading

LLM Series Super Detailed Analysis (Part 9): MobileLLM: Optimizing Language Models with 1B Parameters

What are the top conferences in the field of NLP?

0. Preface

1. Paper Overview

2. Mixtral 8x7B Model Architecture and Computational Flow

2.1 Model Architecture

2.2 SMoE Layer Implementation2.2.1 Single Expert Implementation

2.2.2 Hybrid Expert Implementation

2.3 SMoE Calculation Process

2.3.1 Gating process

2.3.2 Expert process

2.4 Router Load Balence 计算

2.4.1 Switch Transformers Load Balance Loss

2.4.2 Mixtral Load Balance Loss Calculation Process

2.4.3 Manual Load Balancing

3. Mixtral 8x7B parameter calculation

3.1 Original paper description

3.2 Model parameter calculation

4. MoE extension

4.1 MegaBlocks

4.2 GShard

4.3 DeepSpeed-MoE

4.4 LLaMA-MoE

5. Mixtral 8x7B Summary & Further Reading

Reference

Content belongs to the column

Hand tear LLM

Master the large model technology

Recommended reading

LLM Series Super Detailed Analysis (Part 9): MobileLLM: Optimizing Language Models with 1B Parameters

What are the top conferences in the field of NLP?

2.2 SMoE Layer Implementation
2.2.1 Single Expert Implementation