不同梯度下降算法的比较及Python实现
少年不识愁滋味,爱上层楼。爱上层楼,为赋新词强说愁。而今识尽愁滋味,欲说还休。欲说还休,却道天凉好个秋。 --- 辛弃疾 《丑奴儿》
梯度下降法是深度学习中常用的一阶优化算法。其逻辑清晰,实现简单,且当目标函数是凸函数时,梯度下降法求得的解是全局最优解。本文拟从算法介绍到算法实现方面进行一个简单梳理作为笔记留存,方便日后查阅,若有纰漏,欢迎指正。由于不同梯度下降法的算法介绍文章汗牛充栋,所以本文主要侧重在算法实现上。
那当我们在谈论梯度下降时,我们究竟在谈论什么?一般而言,根据时间线排列,常见的梯度下降法有:
- Batch Gradient Descent(BGD,批量梯度下降)
- Stochastic Gradient Descent(SGD,随机梯度下降)
- Mini-Batch Gradient Descent(MBGD,小批量梯度下降)
- Moment Gradient Descent(MGD,动量梯度下降)
- Adaptive Gradient Descent(AdaGrad,自适应梯度下降,2011)
- Adaptive Delta Gradient Descent(AdaDelta,自适应调整梯度下降, 2012)
- Root Mean Square Prop(RMSProp,均方根支撑, 2012)
- Nesterov Accelerated Gradient Descent(NAG,Nesterov加速梯度下降,2013)
- Adaptive Moment Estimation(Adam,自适应矩估计,2014)
- Adaptive Moment Estimation Max(AdaMax, 2015)
- Nesterov Adaptive Moment Estimation(Nadam,Nesterov加速自适应矩估计,2016)
- Adam & RMSProp Gradient Descent (AMSGrad, 2018)
\gg Batch Gradient Descent
批量梯度下降法是梯度下降最原始的形式,其在全部训练集上计算损失函数 J_{\theta} 关于参数 \theta 的梯度。一个常规的梯度下降的过程如下:
- 构造假设函数 h_{\theta}(x)
h_{\theta}(x_1, x_2, ..., x_n) = \theta_0 + \theta_1 x_1 + ... + \theta_n x_n = \sum_{i=0}^{n}\theta_{i}x_{i},x_0 = 1
2. 构造损失函数 J(\theta)
J(\theta_0, \theta_1, ..., \theta_n) = \frac{1}{2m}\sum_{j=0}^{m} (h_{\theta}^{j}(x_0, x_1, ..., x_n) - y_{j}) ^ 2
3. 判断程序是否提前终止
计算损失函数的值 J_{\theta}^{t+1} ,并与前值 J_{\theta}^{t} 进行差值运算,当其绝对值小于某个设定的阈值 \epsilon ,则提前终止程序,当前的 \theta 值即为最终结果,若否,跳入步骤4
4. 计算损失函数 J(\theta) 关于参数 \theta 的梯度
\frac{\partial}{\partial \theta_i} J(\theta_0, \theta_1, ..., \theta_n)=\frac{1}{m}\sum_{j=0}^{m}(h_{\theta}^{j}(x_0, x_1, ..., x_n) - y_{j})x_{i}^{j}
5. 更新参数 \theta 的表达式,并返回步骤1
\theta_i = \theta_i - \frac{\eta }{m}\sum_{j=0}^{m}(h_{\theta}^{j}(x_0, x_1, ..., x_n) - y_j)x_{i}^{j}
当我们根据以上逻辑编写程序时,通常需要初始化几个变量:
- 学习率(learning_rate)
学习率是控制梯度下降幅度的参数,亦称步长,学习率设置过大会阻碍收敛并导致损失函数在最小值附近波动甚至发散;学习率太小又会导致收敛速度缓慢,尤其是在迭代后期,当梯度变动很小的时候,整个收敛过程会变得很缓慢
- 初始权重(theta)
初始权重的个数等于原始样本中特征值的个数加1,其中新增的1个参数主要考虑偏置项( bias )带来的影响
- 程序终止条件(max_iteration_number / tolerance)
- 最大迭代次数:防止结果不收敛时,对程序进行强制终止
- 误差容忍度:当结果改善的变动低于某个阈值时,程序提前终止
class BatchGradientDescent:
def __init__(self, eta=0.01, n_iter=1000, tolerance=0.001):
self.eta = eta
self.n_iter = n_iter
self.tolerance = tolerance
def fit(self, X, y):
n_samples = len(X)
X = np.c_[np.ones(n_samples), X] # 增加截距项
n_features = X.shape[-1]
self.theta = np.ones(n_features)
self.loss_ = [0]
self.i = 0
while self.i < self.n_iter:
self.i += 1
errors = X.dot(self.theta) - y
loss = 1 / (2 * n_samples) * errors.dot(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
else:
gradient = 1 / n_samples * X.T.dot(errors)
self.theta -= self.eta * gradient
return self批量梯度下降法由于使用了全部样本进行训练,所以当损失函数是凸函数时,理论上可以找到全局最优解,但当训练样本很大时,其训练速度会非常慢,不适用于在线学习的一些项目。为了解决这个问题,随机梯度下降算法被提出。
\gg Stochastic Gradient Descent
为了避免训练速度过慢,随机梯度下降法在训练过程中每次仅针对一个样本进行训练,但进行多次更新。在每一轮新的更新之前,需要对数据样本进行重新洗牌(shuffle)。
class StochasticGradientDescent(BatchGradientDescent):
def __init__(self, shuffle=True, random_state=None, **kwargs):
super(StochasticGradientDescent, self).__init__(**kwargs)
self.shuffle = shuffle
if random_state:
np.random.seed(random_state)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.loss_ = [0]
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y) # 重新排序
errors = []
for xi, yi in zip(X, y):
error_i = xi.dot(self.theta) - yi
errors.append(error_i**2)
gradient_i = xi.T.dot(error_i) # 单个样本的梯度
self.theta -= self.eta * gradient_i
loss = 1/2 * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self
@staticmethod
def _shuffle(X, y):
location = np.random.permutation(len(y))
return X[location], y[location]随机梯度下降法在更新过程中由于是针对单个样本,所以其迭代的方向有时候并不是整体最优的方向,同时其方差较大,导致损失函数值的变动并不是规律的递减,更多的情况可能是波动形状的下降。
为了解决批量梯度下降的速度太慢以及随机梯度下降方差变动过大的情况,一种折中的算法--小批量梯度下降算法被提出,其从全部样本中选取部分样本进行迭代训练。并且在每一轮新的迭代开始之前,对全部样本进行Shuffle处理。那么问题来了,为什么进行随机梯度下降时,需要在每一轮更新之前对数据样本进行重新洗牌(shuffle)呢?
class MiniBatchGradientDescent(StochasticGradientDescent):
def __init__(self, batch_size=10, **kwargs):
self.batch_size = batch_size
super(MiniBatchGradientDescent, self).__init__(**kwargs)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.loss_ = [0]
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y)
errors = []
for j in range(0, n_samples, self.batch_size):
mini_X, mini_y = X[j: j + self.batch_size], y[j: j + self.batch_size]
error = mini_X.dot(self.theta) - mini_y # 长度与batch_size的长度一致
errors.append(error.dot(error))
mini_gradient = 1 / self.batch_size * mini_X.T.dot(error) # 小批量样本梯度
self.theta -= self.eta * mini_gradient
loss = 1 / (2 * self.batch_size) * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self以上三种梯度下降算法仅局限于对训练样本进行变更,且每次迭代更新权重时使用的梯度仅作用于当前状态。由于每一期的样本有好有坏,导致迭代过程是曲折波动的,影响了收敛速度。为了降低波动幅度从而加快收敛,各种梯度下降算法的升级版开始出现。由于小批量梯度下降算法是以上三种中的最优选择,所以以下的改进算法均基于小批量梯度下降来说明。
\gg Momentum Gradient Descent
{g}_{t} = \nabla {J_{\theta}(\theta_{t})}
v_{t} = \gamma v_{t-1} + \eta g_{t}
\theta_{t+1} = \theta_{t} - v_{t}
其中,超参数 \gamma 通常设为0.9,velocity 初始化为0
区别于仅使用当前梯度来更新权重的梯度下降法,动量梯度下降法引入了一个新的参数velocity 来表示当前的梯度变动,其本质上是一个指数加权移动平均值,其将历史上每一期的梯度都考虑到了当前的状态中。同时指数加权移动的特性使得当前梯度在参数更新中能够占据更大权重,这也符合我们的一般认知,越接近当下的信息对未来的判断越重要。当衰减超参数 \gamma 远大于学习率 \eta 的时候,在程序迭代过程中,历史梯度的累积值在梯度的更新过程中将会占据主导作用,即使因为噪音的扰动导致当前梯度变化较大,也不会对最终的更新方向产生大的影响。
若当前梯度 \nabla_{\theta}J(\theta) 与上期velocity 方向一致时,本期velocity 项相应增加,参数 \theta 更新幅度加大,加快训练速度;当方向相反时, velocity 项相应减少,参数 \theta 更新幅度缓慢减小,避免了大幅震荡,用一句不太恰当的比喻,动量梯度下降有种“锦上添花,雪中送碳”的意味。
class MomentumGradientDescent(MiniBatchGradientDescent):
def __init__(self, gamma=0.9, **kwargs):
self.gamma = gamma # 当gamma=0时,相当于小批量随机梯度下降
super(MomentumGradientDescent, self).__init__(**kwargs)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.velocity = np.zeros_like(self.theta)
self.loss_ = [0]
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y)
errors = []
for j in range(0, n_samples, self.batch_size):
mini_X, mini_y = X[j: j + self.batch_size], y[j: j + self.batch_size]
error = mini_X.dot(self.theta) - mini_y
errors.append(error.dot(error))
mini_gradient = 1 / self.batch_size * mini_X.T.dot(error)
self.velocity = self.velocity * self.gamma + self.eta * mini_gradient
self.theta -= self.velocity
loss = 1 / (2 * self.batch_size) * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self\gg NesterovAcceleratedGradient
\tilde{g}_{t} = \nabla {J_{\theta}(\theta_{t} - \gamma v_{t-1})}
v_{t} = \gamma v_{t-1} + \eta \tilde{g_{t}}
\theta_{t+1} = \theta_{t} - v_{t}
Nesterov Accelerated Gradient与Momentum Gradient Descent的方法非常相似,二者的差异主要在于计算梯度时所用的参数,一个是纯粹的 \theta ,一个是经过 velocity 调整后的 \tilde{\theta} 。为了便于理解其内在的差异,可以这样想象二者的作用机制:动量梯度下降是利用历史情况对当前状态进行纠偏,防止过度反应;而Nesterov加速下降则依赖于先见之明,对未来的走势进行预判,在事情发生前便进行了内部调整,避免出现极端情况。再给个不太恰当的比喻,Momentum是亡羊补牢,Nesterov是未雨绸缪。
class NesterovAccelerateGradient(MomentumGradientDescent):
def __init__(self, **kwargs):
super(NesterovAccelerateGradient, self).__init__(**kwargs)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.velocity = np.zeros_like(self.theta)
self.loss_ = [0]
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y)
errors = []
for j in range(0, n_samples, self.batch_size):
mini_X, mini_y = X[j: j + self.batch_size], y[j: j + self.batch_size]
error = mini_X.dot(self.theta - self.gamma * self.velocity) - mini_y
errors.append(error.dot(error))
mini_gradient = 1 / self.batch_size * mini_X.T.dot(error)
self.velocity = self.velocity * self.gamma + self.eta * mini_gradient
self.theta -= self.velocity
loss = 1 / (2 * self.batch_size) * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self虽然动量类梯度下降能够加快程序运行速度,但前述各种梯度下降算法依然只是遵循一个固定的学习速率,这便需要用户对样本的特性有个前瞻性了解以选取一个合适的初始超参数,但合适超参数的选取本身也是一件有挑战的事情,那有没有什么方法来根据具体情况自适应学习率呢?自适应梯度下降算法应运而生。
\gg AdaptiveGradientDescent
\theta_{t+1} = \theta_{t} - \frac{\eta }{\sqrt{diag(G_{t}) + \epsilon I}} \odot g_{t} = \theta_{t} - \frac{\eta }{\sqrt{\sum g_{t}^2 + \epsilon}} \odot g_{t}
G_{t} = \sum_{\tau=1}^{t}{g_{\tau}g_{\tau}^{T}}
其中,矩阵G_{t} 的第 t 个对角元素是前 t 个时刻关于参数 \theta 的历史梯度值的平方和, \epsilon 的作用主要是为了避免分母出现为0的情况,通常初始化为1e-6 。
自适应梯度下降法通过将学习率除以历史梯度值平方和的平方根得到新的学习率从而来优化程序的迭代。那么问题来了,为什么分母部分需要构建成一个均方根(Root Mean Square)形式呢?这里隐含的一个前提是,学习率需为正值且其调整依赖于梯度值,这个梯度值的构成可以是历史梯度值的简单平均抑或是指数加权移动平均。
但回到算法本身,我们会发现,如果最优解需要很多次迭代,随着迭代次数的不断增加,历史梯度的平方和的平方根会越来越大,导致学习率会逐渐收缩到无穷小,大大降低了程序后期的运行效率。所以为了尽量减少迭代次数,我们最好在初始时刻设置一个较大的学习率。
class AdaptiveGradientDescent(MiniBatchGradientDescent):
def __init__(self, epsilon=1e-6, **kwargs):
self.epsilon = epsilon
super(AdaptiveGradientDescent, self).__init__(**kwargs)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.loss_ = [0]
gradient_sum = np.zeros(n_features)
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y)
errors = []
for j in range(0, n_samples, self.batch_size):
mini_X, mini_y = X[j: j + self.batch_size], y[j: j + self.batch_size]
error = mini_X.dot(self.theta) - mini_y
errors.append(error.dot(error))
mini_gradient = 1 / self.batch_size * mini_X.T.dot(error)
gradient_sum += mini_gradient ** 2
adj_gradient = mini_gradient / (np.sqrt(gradient_sum + self.epsilon))
self.theta -= self.eta * adj_gradient
loss = 1 / (2 * self.batch_size) * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self既然有缺点,就要改正。为了避免学习速率随着迭代次数增加逐渐收缩到无穷小的问题,AdaGrad的升级版开始被相继提出,最有代表性的包括AdaDelta和RMSProp。
\gg AdaDelta
E[g^2]_{t} = \gamma E[g^2]_{t-1} + (1-\gamma)g^2_{t}
\Delta \theta_{t} = -\frac{\sqrt{E[\Delta \theta ^2]_{t-1} + \epsilon}}{\sqrt{E[g^2]_{t-1} + \epsilon}} g_{t}
E[\Delta \theta^2]_{t} = \gamma E[\Delta \theta^2]_{t-1} + (1- \gamma)\Delta \theta_{t}^2
\theta_{t+1} = \theta_{t} + \Delta{\theta_{t}}
其中, \gamma 表示衰减参数。
AdaDelta主要的特性在于其虽然考虑了历史的梯度值,但其通过对历史梯度的平方进行指数加权移动平均来减缓梯度的累积效应,进而达到了减缓学习率收缩的速度;同时,其引入了一个作用类似于动量的成分来代替原始的超参数学习率 \eta ,状态变量的自适应性加快了收敛速度
class AdaDelta(MiniBatchGradientDescent):
def __init__(self, gamma=0.95, epsilon=1e-6, **kwargs):
self.gamma = gamma
self.epsilon = epsilon
super(AdaDelta, self).__init__(**kwargs)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.loss_ = [0]
gradient_exp = np.zeros(n_features)
delta_theta_exp = np.zeros(n_features)
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y)
errors = []
for j in range(0, n_samples, self.batch_size):
mini_X, mini_y = X[j: j + self.batch_size], y[j: j + self.batch_size]
error = mini_X.dot(self.theta) - mini_y
errors.append(error.dot(error))
mini_gradient = 1 / self.batch_size * mini_X.T.dot(error)
gradient_exp = self.gamma * gradient_exp + (1 - self.gamma) * mini_gradient ** 2
gradient_rms = np.sqrt(gradient_exp + self.epsilon)
delta_theta = -np.sqrt(delta_theta_exp + self.epsilon) / gradient_rms * mini_gradient
delta_theta_exp = self.gamma * delta_theta_exp + (1 - self.gamma) * delta_theta ** 2
delta_theta_rms = np.sqrt(delta_theta_exp + self.epsilon)
delta_theta = -delta_theta_rms / gradient_rms * mini_gradient
self.theta += delta_theta
loss = 1 / (2 * self.batch_size) * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self\gg RootMeanSquareProp
E[g^2]_{t} = \gamma E[g^2]_{t-1} + (1-\gamma)g_{t}^2
\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{E[g^2]_{t} + \epsilon}}g_{t}
RMSProp的提出也是为了对AdaGrad进行改进,防止学习速率过快的衰减。区别于AdaGrad对历史所有梯度的平方进行累加,RMSProp采用了对历史梯度的平方和进行指数加权移动,来减缓梯度的累积效应,而其与AdaDelta的差异仅仅在于未对学习率进行变动。
class RMSProp(MiniBatchGradientDescent):
def __init__(self, gamma=0.9, epsilon=1e-6, **kwargs):
self.gamma = gamma
self.epsilon = epsilon
super(RMSProp, self).__init__(**kwargs)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.loss_ = [0]
gradient_exp = np.zeros(n_features)
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y)
errors = []
for j in range(0, n_samples, self.batch_size):
mini_X, mini_y = X[j: j + self.batch_size], y[j: j + self.batch_size]
error = mini_X.dot(self.theta) - mini_y
errors.append(error.dot(error))
mini_gradient = 1 / self.batch_size * mini_X.T.dot(error)
gradient_exp = self.gamma * gradient_exp + (1 - self.gamma) * mini_gradient ** 2
gradient_rms = np.sqrt(gradient_exp + self.epsilon)
self.theta -= self.eta / gradient_rms * mini_gradient
loss = 1 / (2 * self.batch_size) * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self\gg AdaptiveMomentEstimation
m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t
v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2
\tilde{m}_{t} = \frac{m_{t}}{1-\beta_1^{t}}
\tilde{v}_{t} = \frac{v_{t}}{1-\beta_2^{t}}
\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{\tilde{v}_{t}} + \epsilon}\tilde{m}_{t}
Adam相对于RMSProp新增了两处改动。其一,Adam使用经过指数移动加权平均的梯度值来替换原始的梯度值;其二,Adam对经指数加权后的梯度值 m_t 和平方梯度值 v_t 都进行了修正,亦即偏差修正(Bias Correction)。那问题来了,为什么要进行偏差修正?
class AdaptiveMomentEstimation(MiniBatchGradientDescent):
def __init__(self, beta_1=0.9, beta_2=0.999, epsilon=1e-6, **kwargs):
self.beta_1 = beta_1
self.beta_2 = beta_2
self.epsilon = epsilon
super(AdaptiveMomentEstimation, self).__init__(**kwargs)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.loss_ = [0]
m_t = np.zeros(n_features)
v_t = np.zeros(n_features)
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y)
errors = []
for j in range(0, n_samples, self.batch_size):
mini_X, mini_y = X[j: j + self.batch_size], y[j: j + self.batch_size]
error = mini_X.dot(self.theta) - mini_y
errors.append(error.dot(error))
mini_gradient = 1 / self.batch_size * mini_X.T.dot(error)
m_t = self.beta_1 * m_t + (1 - self.beta_1) * mini_gradient
v_t = self.beta_2 * v_t + (1 - self.beta_2) * mini_gradient ** 2
m_t_hat = m_t / (1 - self.beta_1 ** self.i) # correction
v_t_hat = v_t / (1 - self.beta_2 ** self.i)
self.theta -= self.eta / (np.sqrt(v_t_hat) + self.epsilon) * m_t_hat
loss = 1 / (2 * self.batch_size) * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self你以为到这里改进空间已经很小,差不多就结束了?Naive!劳动人民的智慧是无穷尽的。一阶矩二阶矩可以整出来,无穷阶矩是不是也可以考虑考虑?
\gg AdaMax
u_t = \beta_{2}^{\infty} v_{t-1} + (1 - \beta_{2}^{\infty})|g_{t}|^\infty =max(\beta_2 v_{t-1}, |g_{t}|)
\theta_{t+1} = \theta_{t} - \frac{\eta}{u{t}}\hat{m}_{t}
AdaMax本质上是一个无穷阶的Adam,其将原来的二阶矩估计扩展到了无穷阶矩。这其中隐含的一个前提是高阶矩往往不稳定,而无穷阶矩却更稳定,具体推导过程请自行Google。同时,AdaMax也无需对变量 u_{t} 进行偏差校正。
class AdaMax(AdaptiveMomentEstimation):
def __init__(self, **kwargs):
super(AdaMax, self).__init__(**kwargs)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.loss_ = [0]
m_t = np.zeros(n_features)
u_t = np.zeros(n_features)
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y)
errors = []
for j in range(0, n_samples, self.batch_size):
mini_X, mini_y = X[j: j + self.batch_size], y[j: j + self.batch_size]
error = mini_X.dot(self.theta) - mini_y
errors.append(error.dot(error))
mini_gradient = 1 / self.batch_size * mini_X.T.dot(error)
m_t = self.beta_1 * m_t + (1 - self.beta_1) * mini_gradient
m_t_hat = m_t / (1 - self.beta_1 ** self.i)
u_t = np.max(np.c_[self.beta_2 * u_t, np.abs(mini_gradient)], axis=1)
self.theta -= self.eta / u_t * m_t_hat
loss = 1 / (2 * self.batch_size) * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self\gg Nadam
\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{\hat{v}_{t}} + \epsilon}(\beta_1 \hat{m}_{t} + \frac{(1-\beta_1)g_{t}}{1-\beta_{1}^t})
根据Nadam的全称Nesterov Accelerated Adaptive Moment Estimation即可联想到其是Nesterov和Adam的结合。具体的推导步骤请参考相关文献,此处不再赘述。
class Nadam(AdaptiveMomentEstimation):
def __init__(self, **kwargs):
super(Nadam, self).__init__(**kwargs)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.loss_ = [0]
m_t = np.zeros(n_features)
v_t = np.zeros(n_features)
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y)
errors = []
for j in range(0, n_samples, self.batch_size):
mini_X, mini_y = X[j: j + self.batch_size], y[j: j + self.batch_size]
error = mini_X.dot(self.theta) - mini_y
errors.append(error.dot(error))
mini_gradient = 1 / self.batch_size * mini_X.T.dot(error)
m_t = self.beta_1 * m_t + (1 - self.beta_1) * mini_gradient
v_t = self.beta_2 * v_t + (1 - self.beta_2) * mini_gradient ** 2
m_t_hat = m_t / (1 - self.beta_1 ** self.i) # correction
v_t_hat = v_t / (1 - self.beta_2 ** self.i)
self.theta -= self.eta / (np.sqrt(v_t_hat) + self.epsilon) * (
self.beta_1 * m_t_hat + (1 - self.beta_1) * mini_gradient / (1 - self.beta_1 ** self.i))
loss = 1 / (2 * self.batch_size) * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self\gg AMSGrad
m_{t} = \beta_{1} m_{t-1} + (1-\beta_{1})g_{t}
v_{t} = \beta_{2}v_{t-1} + (1-\beta_2)g_{t}^2
\hat{v}_{t} = max(\hat{v}_{t-1}, v_{t})
\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{\hat{v}_{t}} + \epsilon}m_{t}
AMSGrad区别于Adam的地方在于:其一,其去除了对变量 m_t 的偏差修正;其二,其使用历史上的平方梯度的最大值替换了指数加权移动平均值来控制学习速率的衰减。
正如作者在文章摘要中指出,虽然AdaGrad方法及其变体在大部分的情况下表现很好,但在其采用指数加权移动平均的平方根的形式来减缓学习率的快速衰减,避免学习率受到最近梯度过大影响的同时,这也导致了其在某些设置中,程序收敛性较差。比如某些小批量样本提供了较大的梯度,但却很少出现,虽然这些大梯度很有用,但是由于采用了指数加权平均,它们的影响很快就消失了,收敛速度也因此下降了。
class AMSGrad(AdaptiveMomentEstimation):
def __init__(self, **kwargs):
super(AMSGrad, self).__init__(**kwargs)
def fit(self, X, y):
X = np.c_[np.ones(len(X)), X]
n_samples, n_features = X.shape
self.theta = np.ones(n_features)
self.loss_ = [0]
m_t = np.zeros(n_features)
v_t = np.zeros(n_features)
v_t_hat = np.zeros(n_features)
self.i = 0
while self.i < self.n_iter:
self.i += 1
if self.shuffle:
X, y = self._shuffle(X, y)
errors = []
for j in range(0, n_samples, self.batch_size):
mini_X, mini_y = X[j: j + self.batch_size], y[j: j + self.batch_size]
error = mini_X.dot(self.theta) - mini_y
errors.append(error.dot(error))
mini_gradient = 1 / self.batch_size * mini_X.T.dot(error)
m_t = self.beta_1 * m_t + (1 - self.beta_1) * mini_gradient
v_t = self.beta_2 * v_t + (1 - self.beta_2) * mini_gradient ** 2
v_t_hat = np.max(np.hstack((v_t_hat, v_t)))
self.theta -= self.eta / (np.sqrt(v_t_hat) + self.epsilon) * m_t
loss = 1 / (2 * self.batch_size) * np.mean(errors)
delta_loss = loss - self.loss_[-1]
self.loss_.append(loss)
if np.abs(delta_loss) < self.tolerance:
break
return self 讲了这么多,让我们来比较一下各梯度下降算法的实际应用情况。曾经听说梯度下降和线性回归更配,那我们也来试一下。构造线性回归表达式如下:
y = 2.3 + 5.1 x_1 - 1.5 x_2
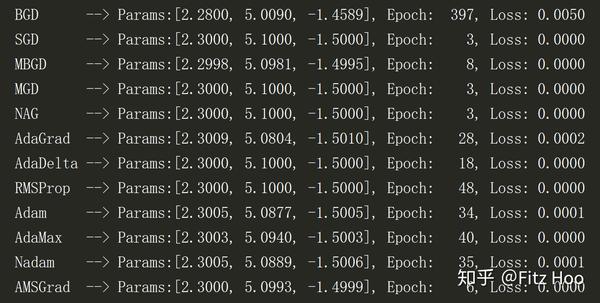
其实我自己在查资料的过程中,发现将梯度过程可视化感觉是更有意思的一件事,有兴趣的小伙伴可以自己动手画画那些梯度介绍文章中出现的动态图。
最后,以上算法的整理结构主要参考了Sebastian Ruder和Raimi Karim的文章 ,在此表示感谢。由于他们整理的相当好,所以本文的侧重点主要是在个人认知的基础上来进行算法实现,从而加深自己对梯度下降的理解深度。
讲完了梯度下降,接着我们就该试着自己搭建一个深度神经网络啦,并尝试用其来进行简单的任务训练,以此来加深我们对神经网络本身作用机制的理解。
以上!
客官,都看到这里了,点个赞再走?
参考资料:
[1] An overview of gradient descent optimization algorithms
[2] 10 Gradient Descent Optimization Algorithms + Cheat Sheet
[3] An Introduction to AdaGrad
[4] 梯度下降小结
[5] Python机器学习




非常有用! 感谢!
其实,我更感兴趣的问题是为何adaptiveGradientDescent中使用的历史梯度的平方的和来控制学习率,但是感觉这里使用历史梯度的平方的平均来控制学习率是不是更合适?这可以看做对梯度的二阶原点距的估计,用来度量梯度估计的分散程度,分散程度越大,学习率就需要调小一点,从后续RMSProp,Adam对adaptiveGradientDescent修正来看,都是对梯度的二阶矩进行一个估计,只不过RMSProp是个有偏估计,在Adam中针对这一点进行了偏差修正,这也是你文中提到的为何进行偏差修正。