生成模型之VAE
2022年第一篇文章,码字不易,求star!
“What I cannot create, I do not understand.” -- Richard Feynman
说起生成模型,大家最容易想到的就是GAN,GAN是通过对抗训练实现的一种隐式生成模型。虽然GAN很强大,但其实还有很多与GAN不同的生成模型,最常见的就是基于最大化似然的模型,变分自动编码器(Variational Autoencoder,VAE)就属于这种类型。这篇文章将介绍VAE的原理和实现。
自动编码器(Autoencoder,AE)
再讲VAE之前,有必要先简单介绍一下自动编码器AE,自动编码器是一种无监督学习方法,它的原理很简单:先将高维的原始数据映射到一个低维特征空间,然后从低维特征学习重建原始的数据。一个AE模型包含两部分网络:
- Encoder:将原始的高维数据映射到低维特征空间,这个特征维度一般比原始数据维度要小,这样就起到压缩或者降维的目的,这个低维特征也往往成为中间隐含特征(latent representation);
- Decoder:基于压缩后的低维特征来重建原始数据;
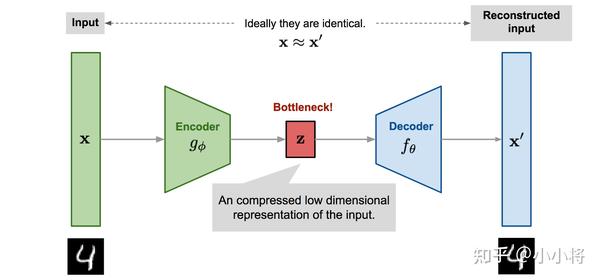
如上图所示,这里g_{\phi}为encoder网络的映射函数(网络参数为\phi),而f_{\theta}为decoder网络的映射函数(网络参数为\theta)。那么对于输入\mathbf{x},可以通过encoder得到隐含特征\mathbf{z}=g_{\phi}(\mathbf{x}),然后decoder可以从隐含特征对原始数据进行重建:\mathbf{x}'=f_{\theta}(\mathbf{z})=f_{\theta}(g_{\phi}(\mathbf{x}))。我们希望重建的数据和原来的数据近似一致的,那么AE的训练损失函数可以采用简单的MSE:
L_\text{AE}(\theta, \phi) = \frac{1}{n}\sum_{i=1}^n (\mathbf{x}^{(i)} - f_\theta(g_\phi(\mathbf{x}^{(i)})))^2 \\
由于训练AE并不需要对数据进行标注,所以AE是一种无监督学习方法。由于压缩后的特征能对原始数据进行重建,所以我们可以用AE的encoder对高维数据进行压缩,这和PCA非常类似,当然得到的隐含特征也可以用来做一些其它工作,比如相似性搜索等。
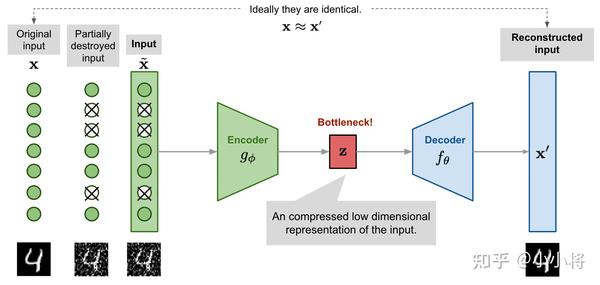
AE有很多变种,比如经典的去噪自编码器(Denoising Autoencoder,DAE),与原始AE不同的是,在训练过程先对输入\mathbf{x}进行一定的扰动,比如增加噪音或者随机mask掉一部分特征。相比AE,DAE的重建难度增加,这也使得encoder学习到的隐含特征更具有代表性。
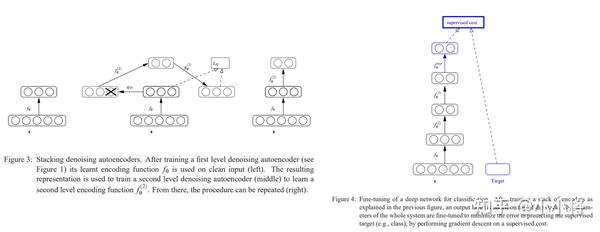
作为一种无监督学习方法,AE除了可以对数据降维,还可以用来对深度网络进行预训练。在深度学习早期,由于存在数据和算力限制,训练深度模型是比较困难的,所以常常采用无监督学习方法先对网络进行预训练,然后在具体的任务上进行有监督finetune,经典的工作如基于DAE的堆叠去噪自编码器(Stacked Denoising Autoencoder,SDA)和基于RBM的深度信念网络(Deep Belief Network,DBN)。
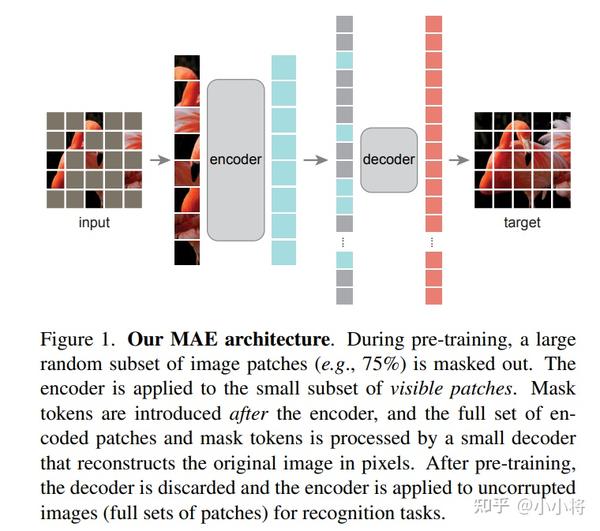
然而,随着大数据的出现(比如包含1.3M图像的ImageNet数据集)以及网络架构的优化(如ResNet的出现),这种训练方式基本被弃用了,目前的主流方式是先在大规模有标注数据集上预训练,然后用预训练初始化的模型来训练具体的任务。由于标注数据存在成本,但收集大规模无标注数据相对容易,所以最近又开始了无监督训练研究的热潮,一些基于对比学习的自监督方法如Moco和SimCLR等已经可以达到和ImageNet有标注监督训练类似的效果。而今年来,随着vision transformer的大爆发,又出现了基于MIM(mask image modeling)的自监督方法,如MAE和SimMIM,它们都是采用和AE类似的设计架构,这让基于AE的无监督训练方法再次卷土重来。
变分自动编码器(Variational Autoencoder,VAE)
VAE虽然名字里也带有自动编码器,但这主要是因为VAE和AE有着类似的结构,即encoder和decoder这样的架构设计。实际上,VAE和AE在建模方面存在很大的区别,从本质上讲,VAE是一种基于变分推断(Variational Inference, Variational Bayesian methods)的概率模型(Probabilistic Model),它属于生成模型(当然也是无监督模型)。在变分推断中,除了已知的数据(观测数据,训练数据)外还存在一个隐含变量,这里已知的数据集记为\mathbf{X}=\{x^{(i)}\}_{i=1}^N由N个连续变量或者离散变量\mathbf{x}组成,而未观测的随机变量记为\mathbf{z},那么数据的产生包含两个过程:
- 从一个先验分布p_{\theta}(\mathbf{z})中采样一个\mathbf{z}^{(i)};
- 根据条件分布p_\theta(\mathbf{x}\vert\mathbf{z}),用\mathbf{z}^{(i)}生成\mathbf{x}^{(i)}。
这里的\theta指的是分布的参数,比如对于高斯分布就是均值和标准差。我们希望找到一个参数\theta^*来最大化生成真实数据的概率:
\theta^{*} = \arg\max_\theta \prod_{i=1}^n p_\theta(\mathbf{x}^{(i)}) \\
这里p_\theta(\mathbf{x}^{(i)})可以通过对\mathbf{z}积分得到:
p_\theta(\mathbf{x}^{(i)}) = \int p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}) p_\theta(\mathbf{z}) d\mathbf{z} \\
而实际上要根据上述积分是不现实的,一方面先验分布p_{\theta}(\mathbf{z})是未知的,而且如果分布比较复杂,对\mathbf{z}穷举计算也是极其耗时的。为了解决这个难题,变分推断引入后验分布p_\theta(\mathbf{z}\vert\mathbf{x})来联合建模,根据贝叶斯公式,后验等于:
p_\theta(\mathbf{z}\vert\mathbf{x}) = \frac{p_\theta(\mathbf{x}\vert\mathbf{z})p_{\theta}(\mathbf{z})}{p_{\theta}(\mathbf{x})} \\
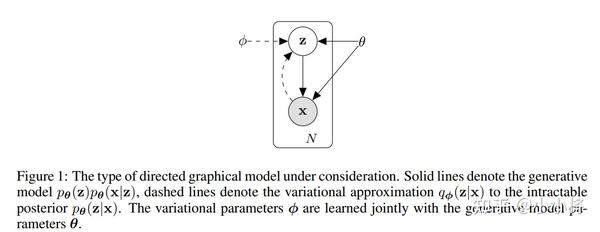
这样的联合建模如上图所示,实线代表的是我们想要得到的生成模型p_\theta(\mathbf{x}\vert\mathbf{z})p_\theta(\mathbf{z}),其中先验分布p_{\theta}(\mathbf{z})往往是事先定义好的(比如标准正态分布),而p_\theta(\mathbf{x}\vert\mathbf{z})可以用一个网络来学习,类比AE的话,如果把\mathbf{z}看成隐含特征,那么这个网络就可以看成一个probabilistic decoder。虚线代表的是对后验分布p_\theta(\mathbf{z}\vert\mathbf{x})的变分估计,记为q_\phi(\mathbf{z}\vert\mathbf{x}),它也可以用一个网络来学习,这个网络可以看成一个probabilistic encoder。可以看到,VAE和AE在架构设计上是类似的,只不过这里probabilistic encoder和probabilistic decoder学习的是两个分布。对于VAE来说,最终目标是得到生成模型即decoder,而encoder只是为了辅助建模,但对于AE来说,常常是为了得到encoder来进行特征提取或者压缩。
建模已经完成,下面我们来推导一下VAE的优化目标。对于估计的后验q_\phi(\mathbf{z}\vert\mathbf{x}),我们希望它接近真实的后验分布p_\theta(\mathbf{z}\vert\mathbf{x}),评估两个分布差异最常用的方式就是计算KL散度(Kullback-Leibler divergence)。对q_\phi(\mathbf{z}\vert\mathbf{x})和p_\theta(\mathbf{z}\vert\mathbf{x})计算KL散度,如下所示:
\begin{aligned} & D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) & \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z} \vert \mathbf{x})} d\mathbf{z} & \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})p_\theta(\mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} d\mathbf{z} & \scriptstyle{\text{; Because }p(z \vert x) = p(z, x) / p(x)} \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \big( \log p_\theta(\mathbf{x}) + \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} \big) d\mathbf{z} & \\ &=\log p_\theta(\mathbf{x}) + \int q_\phi(\mathbf{z} \vert \mathbf{x})\log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} d\mathbf{z} & \scriptstyle{\text{; Because }\int q(z \vert x) dz = 1}\\ &=\log p_\theta(\mathbf{x}) + \int q_\phi(\mathbf{z} \vert \mathbf{x})\log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{x}\vert\mathbf{z})p_\theta(\mathbf{z})} d\mathbf{z} & \scriptstyle{\text{; Because }p(z, x) = p(x \vert z) p(z)} \\ &=\log p_\theta(\mathbf{x}) + \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z} \vert \mathbf{x})}[\log \frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z})} - \log p_\theta(\mathbf{x} \vert \mathbf{z})] &\\ &=\log p_\theta(\mathbf{x}) + D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z})) - \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) & \end{aligned}\\
最终可以得到:
D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) =\log p_\theta(\mathbf{x}) + D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z})) - \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) \\
这里我们适当调整一下上述等式中各个项的位置,可以得到:
\log p_\theta(\mathbf{x}) - D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) = \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) - D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z})) \\
这里\log p_\theta(\mathbf{x})是生成真实数据的对数似然,对于生成模型,我们希望最大化这个对数似然,而D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) )是估计的后验分布和真实分布的KL散度,我们希望最小化该KL散度(KL散度为0时两个分布没有差异),所以上述等式的左边就是联合建模的最大化优化目标,这等价于最大化等式的右边。这个等式的右边又称为Evidence lower bound,简称为ELBO,这主要是因为p_\theta(\mathbf{x})一般称为evidence,而由于KL散度的非负性,所以有下述不等式:
\log p_\theta(\mathbf{x}) \geq \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) - D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z})) \\
所以ELBO是evidence的下限,ELBO是变分推断中经常用到的优化目标。对于VAE,ELBO取负就是其要最小化的训练目标:
\begin{aligned} L_\text{VAE}(\theta, \phi) &= - \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})} \log p_\theta(\mathbf{x}\vert\mathbf{z}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}) ) \\ \theta^{*}, \phi^{*} &= \arg\min_{\theta, \phi} L_\text{VAE} \end{aligned}\\
对于优化目标的第二项,即计算q_\phi(\mathbf{z}\vert\mathbf{x})和p_\theta(\mathbf{z})的KL散度,首先我们必须要对两个分布做一定的假设:
\begin{aligned} &q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) = \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I}) & \\ &p_{\theta}(\mathbf{z}) = \mathcal{N}(\mathbf{z}, 0, \boldsymbol{I}) \end{aligned}\\
即q_\phi(\mathbf{z}\vert\mathbf{x})为各分量独立的多元高斯分布(协方差矩阵为对角矩阵),那么encoder网络预测的就是高斯分布的均值\boldsymbol{\mu}和方差\boldsymbol{\sigma}^2(实际处理时预测\log\boldsymbol{\sigma}^2,因为该值是无约束的)。而先验p_\theta(\mathbf{z})为标准正态分布,这样就变成了计算两个多元高斯分布的KL散度。对于多元高斯分布,其概率密度函数为:
\begin{equation}p(\mathbf{x})=\frac{1}{\sqrt{(2\pi)^n \det(\boldsymbol{\Sigma})}}\exp\left\{-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^{\top}\boldsymbol{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})\right\}\end{equation} \\
对于两个多元高斯分布,其KL散度计算推导如下:
\begin{aligned} \text{KL}(p_1||p_2) &= \text{E}_{p_1}(\log(p_1) - \log(p_2)) \\ &= -\frac{1}{2}\text{E}_{p_1}[\log(\det(\boldsymbol{\Sigma_1}))+(\mathbf{x}-\boldsymbol{\mu_1})^{\top}\boldsymbol{\Sigma}_1^{-1}(\mathbf{x}-\boldsymbol{\mu_1}) - \log(\det(\boldsymbol{\Sigma_2}))-(\mathbf{x}-\boldsymbol{\mu_2})^{\top}\boldsymbol{\Sigma}_2^{-1}(\mathbf{x}-\boldsymbol{\mu_2}) ]\\ &= \frac{1}{2}\log\frac{\det(\boldsymbol{\Sigma_2})}{\det(\boldsymbol{\Sigma_1})} +\frac{1}{2}\text{E}_{p_1}[-(\mathbf{x}-\boldsymbol{\mu_1})^{\top}\boldsymbol{\Sigma}_1^{-1}(\mathbf{x}-\boldsymbol{\mu_1}) +(\mathbf{x}-\boldsymbol{\mu_2})^{\top}\boldsymbol{\Sigma}_2^{-1}(\mathbf{x}-\boldsymbol{\mu_2})] \\ &= \frac{1}{2}\log\frac{\det(\boldsymbol{\Sigma_2})}{\det(\boldsymbol{\Sigma_1})} +\frac{1}{2}\text{E}_{p_1}[-\text{tr}((\mathbf{x}-\boldsymbol{\mu_1})^{\top}\boldsymbol{\Sigma}_1^{-1}(\mathbf{x}-\boldsymbol{\mu_1})) +\text{tr}((\mathbf{x}-\boldsymbol{\mu_2})^{\top}\boldsymbol{\Sigma}_2^{-1}(\mathbf{x}-\boldsymbol{\mu_2}))]\\ &= \frac{1}{2}\log\frac{\det(\boldsymbol{\Sigma_2})}{\det(\boldsymbol{\Sigma_1})} +\frac{1}{2}\text{E}_{p_1}[-\text{tr}(\boldsymbol{\Sigma}_1^{-1}(\mathbf{x}-\boldsymbol{\mu_1})(\mathbf{x}-\boldsymbol{\mu_1})^{\top}) +\text{tr}(\boldsymbol{\Sigma}_2^{-1}(\mathbf{x}-\boldsymbol{\mu_2})(\mathbf{x}-\boldsymbol{\mu_2})^{\top})] \\ &= \frac{1}{2}\log\frac{\det(\boldsymbol{\Sigma_2})}{\det(\boldsymbol{\Sigma_1})} -\frac{1}{2}\text{tr}(\boldsymbol{\Sigma}_1^{-1}\text{E}_{p_1}[(\mathbf{x}-\boldsymbol{\mu_1})(\mathbf{x}-\boldsymbol{\mu_1})^{\top}]) +\frac{1}{2}\text{tr}(\boldsymbol{\Sigma}_2^{-1}\text{E}_{p_1}[(\mathbf{x}-\boldsymbol{\mu_2})(\mathbf{x}-\boldsymbol{\mu_2})^{\top}]) \\ &= \frac{1}{2}\log\frac{\det(\boldsymbol{\Sigma_2})}{\det(\boldsymbol{\Sigma_1})} -\frac{1}{2}\text{tr}(\boldsymbol{\Sigma}_1^{-1}\boldsymbol{\Sigma}_1) +\frac{1}{2}\text{tr}(\boldsymbol{\Sigma}_2^{-1}\text{E}_{p_1}[(\mathbf{x}\mathbf{x}^{\top}-\mathbf{x}\boldsymbol{\mu_2}^{\top}- \boldsymbol{\mu_2}\mathbf{x}^{\top}+\boldsymbol{\mu_2}\boldsymbol{\mu_2}^{\top}])\\ &= \frac{1}{2}\log\frac{\det(\boldsymbol{\Sigma_2})}{\det(\boldsymbol{\Sigma_1})} -\frac{1}{2}n +\frac{1}{2}\text{tr}(\boldsymbol{\Sigma}_2^{-1}(\boldsymbol{\Sigma}_1+\boldsymbol{\mu_1}\boldsymbol{\mu_1}^{\top}-\boldsymbol{\mu_1}\boldsymbol{\mu_2}^{\top}-\boldsymbol{\mu_2}\boldsymbol{\mu_1}^{\top}+\boldsymbol{\mu_2}\boldsymbol{\mu_2}^{\top})) \\ &= \frac{1}{2}\log\frac{\det(\boldsymbol{\Sigma_2})}{\det(\boldsymbol{\Sigma_1})} -\frac{1}{2}n +\frac{1}{2}\text{tr}(\boldsymbol{\Sigma}_2^{-1}\boldsymbol{\Sigma}_1)+\frac{1}{2}(\boldsymbol{\mu_2}-\boldsymbol{\mu_1})^{\top}\boldsymbol{\Sigma}_2^{-1}(\boldsymbol{\mu_2}-\boldsymbol{\mu_1}) \\ &= \frac{1}{2}(\text{tr}(\boldsymbol{\Sigma}_2^{-1}\boldsymbol{\Sigma}_1)+(\boldsymbol{\mu_2}-\boldsymbol{\mu_1})^{\top}\boldsymbol{\Sigma}_2^{-1}(\boldsymbol{\mu_2}-\boldsymbol{\mu_1})-n+\log\frac{\det(\boldsymbol{\Sigma_2})}{\det(\boldsymbol{\Sigma_1})}) \end{aligned}\\
上述公式的推导涉及到一些线性代数的知识,如矩阵的迹运算(tr),如果不明白可以参考这篇文章。根据上述公式,就可以计算出q_\phi(\mathbf{z}\vert\mathbf{x})和p_\theta(\mathbf{z})的KL散度:
\begin{aligned} \text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)})||p_{\theta}(\mathbf{z})) &= \text{KL}(\mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I})||\mathcal{N}(\mathbf{z}, 0, \boldsymbol{I}) )\\ &= \frac{1}{2}\Big(\text{tr}(\boldsymbol{\sigma}^{2(i)}\boldsymbol{I})+(\boldsymbol{\mu}^{(i)})^{\top}\boldsymbol{\mu}^{(i)}-n-\log\det{\boldsymbol{\sigma}^{2(i)}\boldsymbol{I}}\Big) \\ &= \frac{1}{2}\sum_{j=0}^{n}\Big( (\sigma^{(i)}_j)^2+ (\mu^{(i)}_j)^2 - 1- \log((\sigma^{(i)}_j)^2) \Big) \end{aligned}\\
这里n指的多元高斯分布分量的总数,或者说是隐变量\mathbf{z}的元素数量。实际上由于q_\phi(\mathbf{z}\vert\mathbf{x})为各分量独立的多元高斯分布,这个计算可以简化为先计算单独计算各分量的的KL散度(即一元正态分布),然后对各分量的KL散度求和,因为一元正态分布的KL散度相对容易推导:
\begin{aligned}&\text{KL}\Big(\mathcal{N}(\mu,\sigma^2)\Big\Vert \mathcal{N}(0,1)\Big)\\ =&\text{E}_{x \thicksim\mathcal{N}(\mu,\sigma^2)}\Big[\log \frac{e^{-(x-\mu)^2/2\sigma^2}/\sqrt{2\pi\sigma^2}}{e^{-x^2/2}/\sqrt{2\pi}}\Big]\\ =&\text{E}_{x \thicksim\mathcal{N}(\mu,\sigma^2)}\Big[\log (\frac{1}{\sqrt{\sigma^2}}\exp(\frac{1}{2}(x^2-(x-\mu)^2/\sigma^2) )\Big]\\ =&\frac{1}{2}\text{E}_{x \thicksim\mathcal{N}(\mu,\sigma^2)}\Big[-\log \sigma^2+x^2-(x-\mu)^2/\sigma^2 \Big]\\ =& \frac{1}{2}(-\log \sigma^2+\sigma^2 + \mu^2-1) \end{aligned}\\
综上,对于训练数据的一个样本\mathbf{x}^{(i)},其KL散度项的优化目标为:
D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) \| p_\theta(\mathbf{z}) ) =\frac{1}{2}\sum_{j=0}^{n}\Big( (\sigma^{(i)}_j)^2+ (\mu^{(i)}_j)^2 - 1- \log((\sigma^{(i)}_j)^2) \Big) \\
现在我们来分析优化目标的第一项-\mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}),它一般被称为重建误差(reconstruction error),因为p_\theta(\mathbf{x}\vert\mathbf{z})正是给定\mathbf{z}下生成真实数据\mathbf{x}的似然(Likelihood)。对于一个给定的训练样本\mathbf{x}^{(i)},我们可以采蒙特卡洛方法(Monte Carlo method)来估计这个数学期望,即从q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)})多次采样来估计:
-\mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)})}\log p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z})\thickapprox-\frac{1}{L}\sum_{l=1}^{L}(\log p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}^{(i,l)})) \\
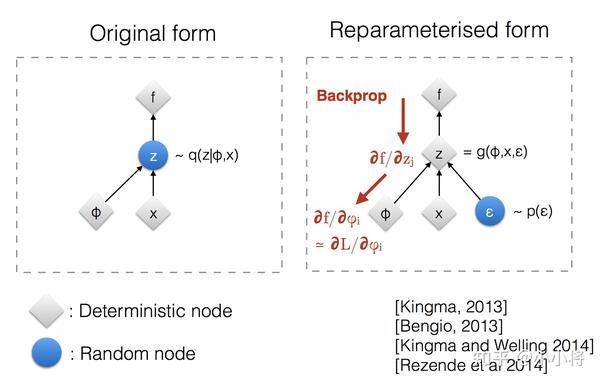
这里的L为采样的总次数,实际上在具体实现上往往L=1,即只随机采样一次(VAE论文中说当训练的mini-batch size足够大时,采样一次是有效的)。另外一个困难的地方,从q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)})采样这个操作是无法计算梯度的,VAE采用一种重参数化(reparameterization)技巧来解决这个问题,具体地,通过引入一个额外的独立随机变量\boldsymbol{\epsilon} \thicksim p(\boldsymbol{\epsilon})来将随机变量\mathbf{z}转变成确定变量:\mathbf{z}=g_{\phi}(\mathbf{x},\boldsymbol{\epsilon})。由于q_\phi(\mathbf{z}\vert\mathbf{x})已经假定为多元高斯分布,使用重采样技巧后则为:
\begin{aligned} \mathbf{z} &\sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) = \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I}) & \\ \mathbf{z} &= \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon} \text{, where } \boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I}) & \scriptstyle{\text{; Reparameterization trick.}} \end{aligned}\\
直观上讲,就是首先从标准正态分布随机采样一个样本,然后乘以encoder预测的标准差,再加上encoder预测的均值,这样就能计算该损失对encoder网络参数的梯度了。
根据建模的数据类型,p_\theta(\mathbf{x}\vert\mathbf{z})分布可以是一个高斯分布也可以是一个伯努利分布,这里以更通用的高斯分布为例。假定p_\theta(\mathbf{x}\vert\mathbf{z})分布也属于一个各分量独立的多元高斯分布:p_\theta(\mathbf{x}\vert\mathbf{z}) = \mathcal{N}(\mathbf{x}; \boldsymbol{\mu}, \boldsymbol{\sigma}^{2}\boldsymbol{I})。由于各个分量独立,所以我们可以单独计算每个分量:
\begin{aligned} \log p(x|z) &= \log \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \\ &= \log \frac{1}{\sqrt{2\pi\sigma^2}} - \frac{1}{2\sigma^2}(x-\mu)^2 \end{aligned}\\
对于这个高斯分布的标准差,我们往往假定它是一个常量,而均值是由decoder预测得出:\boldsymbol{\mu}=f_{\theta}(\mathbf {z})。那么则有:
-\log p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}^{(i,l)}) = C_1+C_2\sum_{d}^{D}(\mathbf{x}^{(i)}_d-(f_{\theta}(\mathbf{z}^{(i,l)}))_d)^2 \\
这里C_1和C_2均是常量,而D是变量\mathbf{x}的维度大小。如果忽略常量C_1的话,那么重建误差其实就是L2损失。上面我们是假定p_\theta(\mathbf{x}\vert\mathbf{z})分布是一个高斯分布,如果p_\theta(\mathbf{x}\vert\mathbf{z})是一个伯努利分布即0-1分布的话,此时decoder直接预测概率值(sigmoid激活函数),重建误差就是交叉熵,:
\log p_{\theta}(\mathbf{x}|\mathbf{z})=\sum_{d}^{D}\Big(\mathbf{x}_d\log(f_{\theta}(\mathbf{z})_d)+(1-\mathbf{x}_d)\log(1-f_{\theta}(\mathbf{z})_d)\Big) \\
根据上述分析,对给定的一个训练样本\mathbf{x}^{(i)},其训练损失(假定是高斯分布)为:
\begin{aligned} L_\text{VAE}(\theta, \phi, \mathbf{x}^{(i)}) &= - \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)})} \log p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) \| p_\theta(\mathbf{z}) ) \\ &\thickapprox-\frac{1}{L}\sum_{l=1}^{L}(\log p_\theta(\mathbf{x}^{(i)}\vert\mathbf{z}^{(i,l)})) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) \| p_\theta(\mathbf{z}) ) \\ &=\frac{C}{L}\sum_{l=1}^{L}\sum_{d}^{D}(\mathbf{x}^{(i)}_d-(f_{\theta}(\mathbf{z}^{(i,l)}))_d)^2 + \frac{1}{2}\sum_{j=0}^{n}\Big( (\sigma^{(i)}_j)^2+ (\mu^{(i)}_j)^2 - 1- \log((\sigma^{(i)}_j)^2) \Big) \end{aligned}\\
如果把KL散度项看到一个正则化的话,那么VAE的损失函数就是重建误差+正则化,这样VAE就可以看成是一个加了约束的AE。VAE的整个训练流程如下所示:输入\mathbf{x},encoder首先计算出后验分布的均值和标准差,然后通过重采样方法采样得到隐变量\mathbf{z},然后送入decoder得到重建的数据\mathbf{x}'。
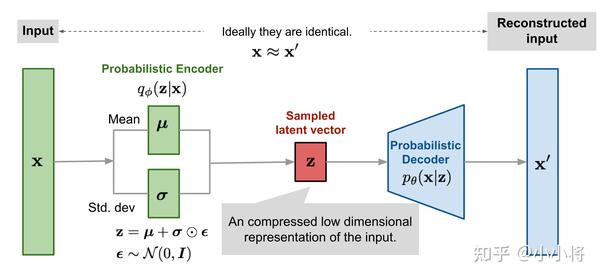
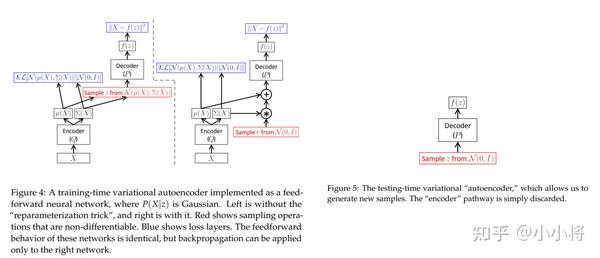
训练完成后,我们就得到生成模型p_\theta(\mathbf{x}\vert\mathbf{z})p_\theta(\mathbf{z}),其中p_\theta(\mathbf{x}\vert\mathbf{z})就是decoder网络,而先验p_\theta(\mathbf{z})为标准正态分布,我们从p_\theta(\mathbf{z})随机采样一个\mathbf{z},送入decoder网络,就能生成与训练数据\mathbf{X}类似的样本。
CVAE
条件变分自编码器(Conditional Variational Autoencoder,CVAE)是VAE的一个变种,相比VAE,CVAE要估计的是一个条件分布p_{\theta}(\mathbf{x}|\mathbf{y}),同样地,我们引入隐变量\mathbf{z}来进行变分推断。此时,给定一个输入\mathbf{y},从先验分布p_{\theta}(\mathbf{z}|\mathbf{y})中采样一个\mathbf{z},然后根据分布p_{\theta}(\mathbf{x}|\mathbf{z},\mathbf{y})生成一个样本\mathbf{x},因而这里要求解的生成模型是p_{\theta}(\mathbf{z}|\mathbf{y})p_{\theta}(\mathbf{x}|\mathbf{z},\mathbf{y})。这个生成模型可以用两个网络来学习,其中一个网络来学习先验分布p_{\theta}(\mathbf{z}|\mathbf{y}),另外一个网络来学习条件分布p_{\theta}(\mathbf{x}|\mathbf{z},\mathbf{y})。在VAE,我们假定先验p_{\theta}(\mathbf{z})为标准正态分布,因为不需要单独的网路来学习;而在CVAE中,先验分布p_{\theta}(\mathbf{z}|\mathbf{y})是一种条件先验,如果假定\mathbf{z}是独立与\mathbf{y}的话,那么此时先验分布p_{\theta}(\mathbf{z}|\mathbf{y})=p_{\theta}(\mathbf{z}),更进一步地也可以简化认为先验为标准正态分布。 同样地,我们另外采用一个网络q_{\phi}(\mathbf{z}|\mathbf{x},\mathbf{y})来估计后验分布p_{\theta}(\mathbf{z}|\mathbf{x},\mathbf{y})。同样地,我们可以推导出ELBO:
\log p_{\theta}(\mathbf{x}|\mathbf{y}) \geq \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x},\mathbf{y})}\log p_\theta(\mathbf{x}\vert\mathbf{z},\mathbf{y}) - D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x},\mathbf{y}) \| p_\theta(\mathbf{z}\vert \mathbf{y})) \\
那么对于CVAE,其优化目标为:
\begin{aligned} L_\text{CVAE}(\theta, \phi) &= - \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x},\mathbf{y})} \log p_\theta(\mathbf{x}\vert\mathbf{z}, \mathbf{y}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}, \mathbf{y}) \| p_\theta(\mathbf{z}\vert \mathbf{y}) ) \\ \theta^{*}, \phi^{*} &= \arg\min_{\theta, \phi} L_\text{CVAE} \end{aligned}\\
对于上述优化目标的处理,同样地可以采用和VAE一样的分析过程,这里不再详细展开,具体见CVAE论文。下图为CVAE的一种实现方式(这里先验简化为标准正态分布):
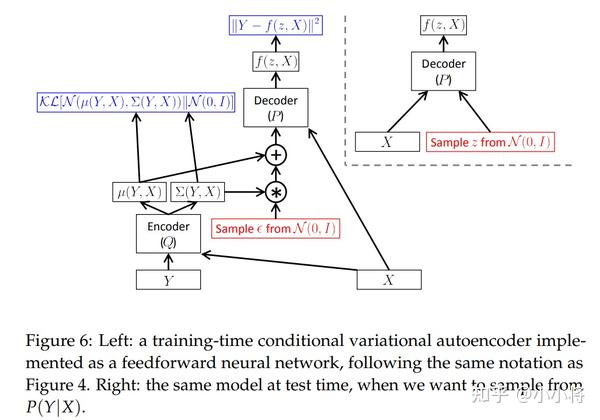
对于VAE和CVAE,它们最重要的区别是数据是如何生成的,对于VAE,数据的产生认为是p_\theta(\mathbf{x}\vert\mathbf{z})p_\theta(\mathbf{z}),而对于CVAE,其数据的产生是p_{\theta}(\mathbf{z}|\mathbf{y})p_{\theta}(\mathbf{x}|\mathbf{z},\mathbf{y}),不同的数据产生方式导致了不同的建模方式和ELBO,但两者用的变分推断理论是一致的。
VAE的代码实现
这里以MNIST数据集为例用PyTorch实现一个简单的VAE生成模型,由于MNIST数据集为灰度图,而且大部分像素点为0(黑色背景)或者白色(255,前景),所以这里可以将像素值除以255归一化到[0, 1],并认为像素值属于伯努利分布,重建误差采用交叉熵。 首先是构建encoder,这里用简单的两层卷积和一个全连接层来实现,encoder给出隐变量的mu和log_var:
class Encoder(nn.Module):
"""The encoder for VAE"""
def __init__(self, image_size, input_dim, conv_dims, fc_dim, latent_dim):
super().__init__()
convs = []
prev_dim = input_dim
for conv_dim in conv_dims:
convs.append(nn.Sequential(
nn.Conv2d(prev_dim, conv_dim, kernel_size=3, stride=2, padding=1),
nn.ReLU()
))
prev_dim = conv_dim
self.convs = nn.Sequential(*convs)
prev_dim = (image_size // (2 ** len(conv_dims))) ** 2 * conv_dims[-1]
self.fc = nn.Sequential(
nn.Linear(prev_dim, fc_dim),
nn.ReLU(),
)
self.fc_mu = nn.Linear(fc_dim, latent_dim)
self.fc_log_var = nn.Linear(fc_dim, latent_dim)
def forward(self, x):
x = self.convs(x)
x = torch.flatten(x, start_dim=1)
x = self.fc(x)
mu = self.fc_mu(x)
log_var = self.fc_log_var(x)
return mu, log_var对于decoder,基本采用对称的结构,这里用反卷积来实现上采样,decoder根据隐变量重构样本或者生成样本:
class Decoder(nn.Module):
"""The decoder for VAE"""
def __init__(self, latent_dim, image_size, conv_dims, output_dim):
super().__init__()
fc_dim = (image_size // (2 ** len(conv_dims))) ** 2 * conv_dims[-1]
self.fc = nn.Sequential(
nn.Linear(latent_dim, fc_dim),
nn.ReLU()
)
self.conv_size = image_size // (2 ** len(conv_dims))
de_convs = []
prev_dim = conv_dims[-1]
for conv_dim in conv_dims[::-1]:
de_convs.append(nn.Sequential(
nn.ConvTranspose2d(prev_dim, conv_dim, kernel_size=3, stride=2, padding=1, output_padding=1),
nn.ReLU()
))
prev_dim = conv_dim
self.de_convs = nn.Sequential(*de_convs)
self.pred_layer = nn.Sequential(
nn.Conv2d(prev_dim, output_dim, kernel_size=3, stride=1, padding=1),
nn.Sigmoid()
)
def forward(self, x):
x = self.fc(x)
x = x.reshape(x.size(0), -1, self.conv_size, self.conv_size)
x = self.de_convs(x)
x = self.pred_layer(x)
return x有了encoder和decoder,然后就可以构建VAE模型了,这里的实现只对隐变量通过重采样方式采样一次,训练损失为KL散度和重建误差(交叉熵)之和:
class VAE(nn.Module):
"""VAE"""
def __init__(self, image_size, input_dim, conv_dims, fc_dim, latent_dim):
super().__init__()
self.encoder = Encoder(image_size, input_dim, conv_dims, fc_dim, latent_dim)
self.decoder = Decoder(latent_dim, image_size, conv_dims, input_dim)
def sample_z(self, mu, log_var):
"""sample z by reparameterization trick"""
std = torch.exp(0.5 * log_var)
eps = torch.randn_like(std)
return mu + eps * std
def forward(self, x):
mu, log_var = self.encoder(x)
z = self.sample_z(mu, log_var)
recon = self.decoder(z)
return recon, mu, log_var
def compute_loss(self, x, recon, mu, log_var):
"""compute loss of VAE"""
# KL loss
kl_loss = (0.5*(log_var.exp() + mu ** 2 - 1 - log_var)).sum(1).mean()
# recon loss
recon_loss = F.binary_cross_entropy(recon, x, reduction="none").sum([1, 2, 3]).mean()
return kl_loss + recon_loss模型训练完成,可以从标准正态分布随机采样,然后生成新的样本,下图为一些模型生成的样本:

VAE虽然主要用于生成,但是作为一种无监督学习方法,也能用于提取特征,下图为从MNIST验证集中提取的中间隐含层特征(encoder属于的mu)的TSNE可视化,可以看到不同类别的隐含特征具有一定的区分度:
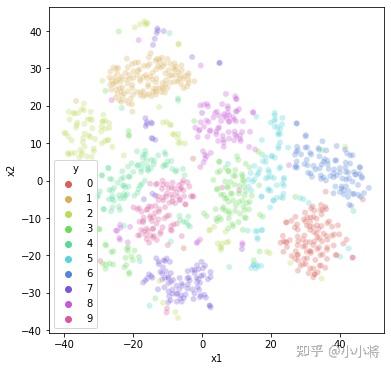
这里额外要提的一点,VAE模型比较容易出现posterior collapse问题,简单来说,就是由于decoder足够强大,可以不依赖隐变量而直接学习到了数据分布,此时:q_{\phi}(\mathbf{z}|\mathbf{x})=p_{\theta}(\mathbf{z}),p_{\theta}(\mathbf{x}|\mathbf{z})=p_{\theta}(\mathbf{x})。这对生成模型没有太大的问题,但是如果你用VAE提取特征的话,就不行了,因为隐变量和原始数据之间没有联系了。这个问题具体可以看看这篇文章Understanding Posterior Collapse in Generative Latent Variable Models。对于posterior collapse问题,也有很多改进方案来解决或者避免,比如VQ-VAE,后面会有新的文章来讲解。
代码的实现放在github上,具体见GitHub - xiaohu2015/nngen
总结
这篇文章简单讲述了自动编码器的原理,并重点介绍了VAE模型的原理以及它和AE之间的联系,最后给出了一个具体的VAE代码实例。VAE模型涉及比较复杂的数学建模,理解它需要花费一定的精力,这里特别感谢一些优秀的文章(见参考)。
参考
- Lilian Weng blog: From Autoencoder to Beta-VAE
- Auto-encoding variational bayes
- Tutorial on variational autoencoders
- 变分自编码器(一):原来是这么一回事
- 变分自编码器(二):从贝叶斯观点出发
- 变分自编码器(五):VAE + BN = 更好的VAE
- A Beginner's Guide to Variational Methods: Mean-Field Approximation
- Understanding Variational Autoencoders (VAEs)
- CVAE: Learning Structured Output Representation using Deep Conditional Generative Models
- PyTorch-VAE
- https://keras.io/examples/generative/vae/
- https://github.com/jojonki/AutoEncoders/blob/master/vae.ipynb





讲得太好啦,就像把憋了一周的答辩拉出来了一样通畅!
有个疑问,在VAE刚开始的似然函数p(x)定义的时候,说p(z)是未知的,不好做积分,但是引入后验概率后又说p(z)是事先定义好的,这个地方该怎么理解呢?
同问![[发呆]](https://pic2.zhimg.com/v2-7f09d05d34f03eab99e820014c393070.png)
同样的疑惑,咋理解![[发呆]](https://pic2.zhimg.com/v2-7f09d05d34f03eab99e820014c393070.png)
写的非常好,感谢
优秀
太美妙了!
VAE中, P\theta( x|z ) 与 P\theta (z|x) 中的 P\theta 不应该一个是decoder 一个是 encoder 吗? 为何用同一样的符号呢? 他们的输入输出完全相反啊? 求解答,谢谢
大神您好,请教一下为什么encoder中隐变量通过全连接层就可以得到均值和方差,期间好像并没有对隐变量的mean()操作或者求方差的操作
好的,谢谢