Small changes; big differences
小改动；大差异

Upcoming 5G wireless communications systems will likely be required to support much wider bandwidths (200MHz and larger) than the 4G systems used today, along with large antenna arrays, enabled by higher carrier frequencies, that will make it possible to build much smaller antenna elements. These so-called massive MIMO applications, together with more stringent latency requirements, will increase design complexity by an order of magnitude.
即将推出的 5G 无线通信系统可能需要支持比目前使用的 4G 系统更宽的带宽（200MHz 或更大），以及由更高载波频率支持的大型天线阵列，这将使构建更小的天线元件成为可能。这些所谓的大规模 MIMO 应用，加上更严格的延迟要求，将使设计复杂性增加一个数量级。

Moving to 20nm not only enables the higher integration capabilities, improved fabric performance and lower power consumption that come with any geometry node migration, but greatly enhanced features that directly support DFE applications. For example, a complete 8Tx/8Rx DFE system with instantaneous bandwidth of 80-100MHz can fit in a single midrange UltraScale FPGA, while a two-chip solution is necessary on the 7 Series architecture.
转向 20nm 不仅可以实现任何几何节点迁移带来的更高集成能力、改进的结构性能和更低的功耗，而且还大大增强了直接支持 DFE 应用的功能。例如，瞬时带宽为 80-100MHz 的完整 8Tx/8Rx DFE 系统可以安装在单个中端 UltraScale FPGA 中，而 7 系列架构则需要两芯片解决方案。

Xilinx has significantly increased the clocking and routing resources in the UltraScale architecture which enables higher device utilisation, especially for high-clock-rate designs. In effect, routing congestion is reduced and designers can achieve better design packing and LUT utilisation; in particular, LUT/SRL compression is more efficient. This is an interesting fabric feature that users can exploit to better pack their designs and consequently optimise resource utilisation as well as dynamic power consumption, which can be reduced by a factor of up to 1.7 for the related logic.
Xilinx 显着增加了 UltraScale 架构中的时钟和布线资源，从而实现了更高的器件利用率，特别是对于高时钟速率设计。实际上，布线拥塞减少了，设计人员可以实现更好的设计封装和 LUT 利用率；特别是，LUT/SRL 压缩效率更高。这是一个有趣的结构功能，用户可以利用它来更好地封装他们的设计，从而优化资源利用率以及动态功耗，相关逻辑的功耗最多可以降低 1.7 倍。

The clocking architecture and Configurable Logic Block (CLB) also contribute to better device utilisation in the UltraScale devices. Although the CLB is still based on that of the 7 Series architecture, there is now a single slice per CLB (instead of two), integrating eight, six-input LUTs and 16 flip-flops. The carry chain is consequently 8 bits long and a wider output multiplexer is available. In addition, Xilinx has also increased the control-set resources (that is, the clock, clock-enable and reset signals shared by the storage elements within a CLB).
时钟架构和可配置逻辑块 (CLB) 也有助于提高 UltraScale 器件的器件利用率。尽管 CLB 仍然基于 7 系列架构，但现在每个 CLB 有一个片（而不是两个），集成了八个六输入 LUT 和 16 个触发器。因此，进位链为 8 位长，并且可以使用更宽的输出多路复用器。此外，Xilinx 还增加了控制集资源（即 CLB 内存储元件共享的时钟、时钟使能和复位信号）。

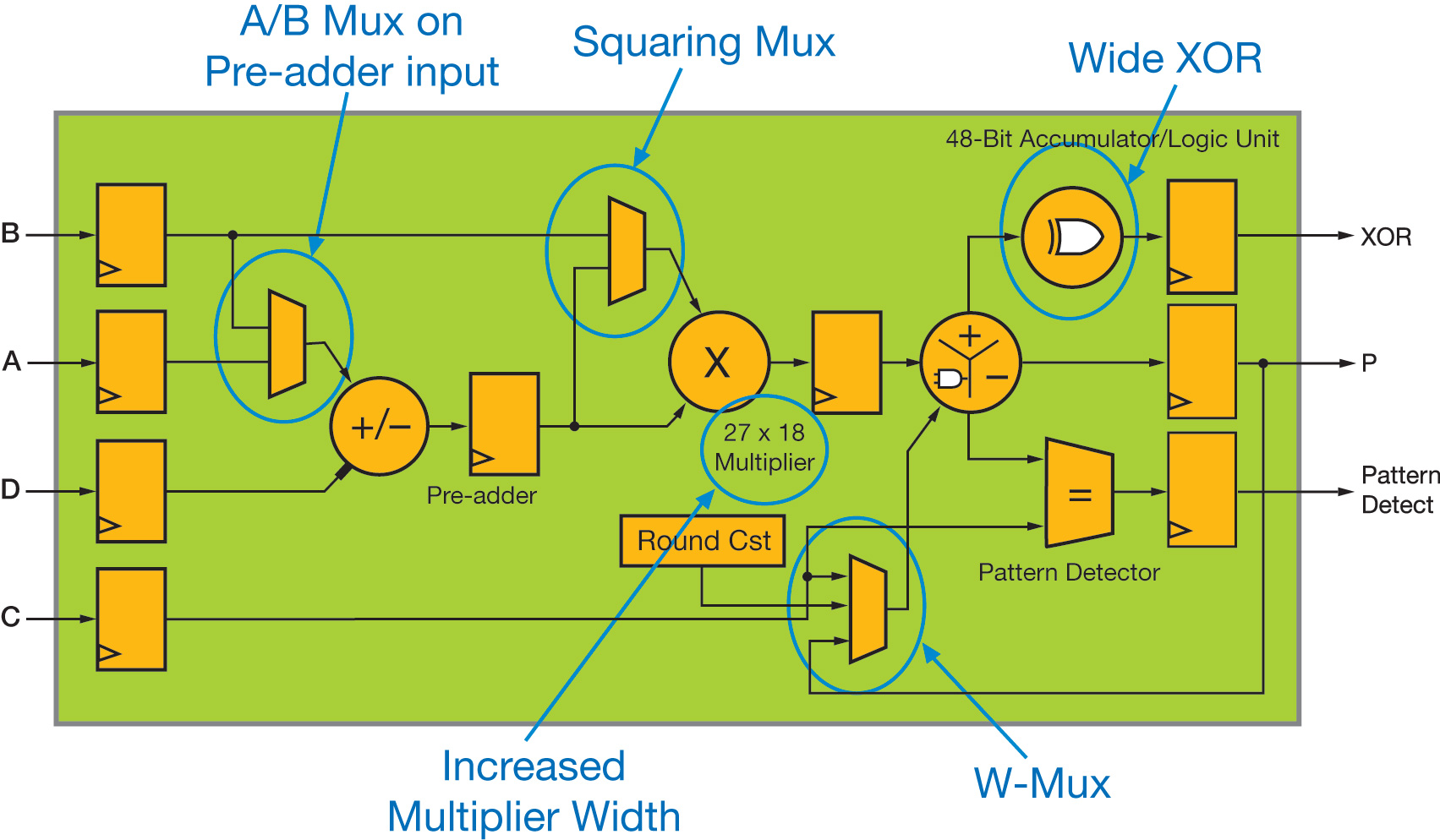
Figure 1 - High-level functional view of the UltraScale DSP48 slice
图 1 - UltraScale DSP48 Slice 的高级功能视图

However, it is essentially the improvements to the DSP48 slice and Block RAM that have the most impact on radio design architectures. Figure 1 highlights the functional enhancements compared with the 7 Series slice (DSP48E1).
然而，本质上对无线电设计架构影响最大的是 DSP48 Slice 和 Block RAM 的改进。图 1 突出显示了与 7 系列 Slice (DSP48E1) 相比的功能增强。

Floating-point support 浮点支持

Increasing the multiplier size from 25x18 to 27x18 has minimal impact on the silicon area of the DSP48 slice, but significantly improves the support for floating-point arithmetic. First, it is worth pointing out that the DSP48E2 can in effect support up to 28x18-bit or 27x19-bit signed multiplication, achieved by using the C input to process the additional bit.
将乘法器尺寸从 25x18 增加到 27x18 对 DSP48 Slice 的硅面积影响最小，但显着提高了对浮点运算的支持。首先，值得指出的是，DSP48E2 实际上可以支持高达 28x18 位或 27x19 位有符号乘法，这是通过使用 C 输入处理附加位来实现的。

This makes it possible to implement a 28x18-bit multiplier with a single DSP48E2 slice and 18 LUT/flip-flop pairs. The same applies for a 27x19-bit multiplier, using 27 additional LUT/flip-flop pairs. In both cases, convergent rounding of the result can still be supported through the W-mux.
这使得使用单个 DSP48E2 Slice 和 18 个 LUT/触发器对实现 28x18 位乘法器成为可能。这同样适用于使用 27 个附加 LUT/触发器对的 27x19 位乘法器。在这两种情况下，结果的收敛舍入仍然可以通过 W-mux 支持。

A double-precision floating-point multiplication involves the integer product of the 53-bit unsigned mantissas of both operators. Although a 52-bit value (m) is stored in the double-precision floating-point representation, it describes the fractional part of the unsigned mantissa, and it is actually the normalised 1+m values, which need to be multiplied together, hence the additional bit required by the multiplication. Taking into account the fact that the MSBs of both 53-bit operands are equal to 1, and appropriately splitting the multiplication to optimally exploit the DSP48E2 26x17-bit unsigned multiplier and its improved capabilities (e.g., the true three-input 48-bit adder enabled by the W-mux), it can be shown that the 53x53-bit unsigned multiplication can be built with only six DSP48E2 slices and a minimal amount of external logic.
双精度浮点乘法涉及两个运算符的 53 位无符号尾数的整数乘积。虽然52位值（m）以双精度浮点表示形式存储，但它描述的是无符号尾数的小数部分，它实际上是归一化的1+m值，需要相乘，因此乘法所需的附加位。考虑到两个 53 位操作数的 MSB 都等于 1，并适当地分割乘法以最佳地利用 DSP48E2 26x17 位无符号乘法器及其改进的功能（例如，真正的三输入 48 位加法器）由 W-mux 启用），可以看出，只需 6 个 DSP48E2 Slice 和最少量的外部逻辑即可构建 53x53 位无符号乘法。

The 27x18 multiplier of the DSP48E2 is also very useful for applications based on fused data paths. The concept of a fused multiply-add operator has been recently added to the IEEE floating-point standard. Basically, it consists of building the floating-point operation A*B+C, without explicitly rounding, normalising and de-normalising the data between the multiplier and the adder. These functions are indeed very costly when using traditional floating-point arithmetic and account for the greatest part of the latency. This concept may be generalised to build sum-of-products operators, which are common in linear algebra (matrix product, Cholesky decomposition). Consequently, such an approach is quite efficient for applications where cost or latency are critical, while still requiring the accuracy and dynamic range of the floating-point representation. This is the case in radio DFE applications for which the digital pre-distortion functionality usually requires some hardware-acceleration support to improve the update rate of the nonlinear filter coefficients. You can then build one or more floating-point MAC engines in the FPGA fabric to assist the coefficient-estimation algorithm running in software (e.g. on one of the ARM Cortex-A9 cores of the Zynq SoC).
DSP48E2 的 27x18 乘法器对于基于融合数据路径的应用也非常有用。融合乘加运算符的概念最近已添加到 IEEE 浮点标准中。基本上，它包括构建浮点运算 A*B+C，无需显式舍入、标准化和反标准化乘法器和加法器之间的数据。当使用传统的浮点运算时，这些函数确实非常昂贵，并且占延迟的最大部分。这个概念可以推广到构建乘积和运算符，这在线性代数（矩阵乘积、Cholesky 分解）中很常见。因此，这种方法对于成本或延迟至关重要的应用程序非常有效，同时仍然需要浮点表示的准确性和动态范围。无线电 DFE 应用就是这种情况，其中数字预失真功能通常需要一些硬件加速支持，以提高非线性滤波器系数的更新速率。然后，您可以在 FPGA 结构中构建一个或多个浮点 MAC 引擎，以协助在软件中运行的系数估计算法（例如，在 Zynq SoC 的 ARM Cortex-A9 内核之一上）。

For such arithmetic structures, it has been shown that a slight increase of the mantissa width from 23 to 26 bits can provide even better accuracy compared with a true single-precision floating-point implementation, but with reduced latency and footprint. The UltraScale architecture is again well adapted for this purpose, since it takes only two DSP48 slices to build a single-precision fused multiplier, whereas three are required on 7 Series devices with additional fabric logic.
对于此类算术结构，事实证明，与真正的单精度浮点实现相比，将尾数宽度从 23 位稍微增加到 26 位可以提供更好的精度，但延迟和占用空间会减少。 UltraScale 架构再次非常适合此目的，因为它只需要两个 DSP48 片即可构建单精度融合乘法器，而具有附加结构逻辑的 7 系列器件则需要三个。

The pre-adder, integrated within the DSP48 slice in front of the multiplier, provides an efficient way to implement symmetric filters that are commonly used in DFE designs to realise the digital upconverter and downconverter functionality.
预加法器集成在乘法器前面的 DSP48 Slice 中，提供了一种有效的方法来实现 DFE 设计中常用的对称滤波器，以实现数字上变频器和下变频器功能。

Fourth input 第四个输入

It is indisputably the addition of a fourth input operand to the ALU, through the extra W-mux multiplexer, which brings the most benefit for radio applications. This operand can typically save 10 to 20% of the DSP48 requirements for such designs compared with the same implementation on a 7 Series device.
毫无疑问，通过额外的 W-mux 多路复用器向 ALU 添加第四个输入操作数，这为无线电应用带来了最大的好处。与 7 系列器件上的相同实现相比，该操作数通常可以节省此类设计 10% 到 20% 的 DSP48 要求。

The W-mux output can only be added within the ALU (subtraction is not permitted), and can be set dynamically as the content of either the C or P register or as a constant value, defined at FPGA configuration (e.g. the constant to be added for convergent or symmetric rounding of the DSP48 output), or simply forced to 0. This allows performing a true three-input operation when the multiplier is used, such as A*B+C+P, A*B+C+PCIN, A*B+P+PCIN, something that is not possible with the 7 Series architecture. Indeed, the multiplier stage generates the last two partial-product outputs, which are then added within the ALU to complete the operation. Therefore, when enabled, the multiplier uses two inputs of the ALU, and a three-input operation cannot be performed on 7 Series devices. Two of the most significant examples that benefit from this additional ALU input are semi-parallel filters and complex multiply-accumulate operators.
W-mux 输出只能在 ALU 内相加（不允许减法），并且可以动态设置为 C 或 P 寄存器的内容或在 FPGA 配置中定义的常量值（例如要设置的常量）。添加用于 DSP48 输出的收敛或对称舍入），或简单地强制为 0。这允许在使用乘法器时执行真正的三输入运算，例如 A*B+C+P、A*B+C+PCIN ，A*B+P+PCIN，这是 7 系列架构不可能实现的。事实上，乘法器级生成最后两个部分乘积输出，然后将其在 ALU 内相加以完成运算。因此，启用后，乘法器使用 ALU 的两个输入，并且无法在 7 系列器件上执行三输入运算。从额外的 ALU 输入中受益的两个最重要的例子是半并行滤波器和复杂的乘法累加运算符。

Linear filters are the most common processing units of any DFE application. When integrating such functionality on Xilinx FPGAs, it is recommended, as far as possible, to implement multichannel filters for which the composite sampling rate (defined as the product of the number of channels by the common signal-sampling frequency of each channel) is equal to the clock rate at which the design is running. In a so-called parallel architecture, each DSP48 slice supports a single filter coefficient per data channel, which greatly simplifies the control logic and hence minimises the design resource utilisation.
线性滤波器是任何 DFE 应用中最常见的处理单元。在 Xilinx FPGA 上集成此类功能时，建议尽可能实现复合采样率（定义为通道数与每个通道的公共信号采样频率的乘积）相等的多通道滤波器设计运行的时钟速率。在所谓的并行架构中，每个 DSP48 Slice 支持每个数据通道一个滤波器系数，这大大简化了控制逻辑，从而最大限度地减少了设计资源利用率。

However, with higher clock-rate capabilities (for example, more than 500MHz on lowest-speed-grade UltraScale devices), and for filters running at a relatively low sampling rate, it is often the case that the clock rate can be selected as a multiple of the composite sampling rate. It’s desirable to increase the clock rate as much as possible to further reduce the design footprint, as well as the power consumption. In such situations, a semi-parallel architecture is built where each DSP48 processes K coefficients per channel, where K is the ratio between the clock rate and the composite sampling rate. The most efficient implementation then consists of splitting the filter into its K phases, each DSP48 processing a specific coefficient of these K phases.
然而，对于更高的时钟速率功能（例如，最低速度等级的 UltraScale 器件上超过 500MHz），并且对于以相对较低的采样速率运行的滤波器，通常可以选择时钟速率作为复合采样率的倍数。人们希望尽可能地提高时钟速率，以进一步减少设计占用空间以及功耗。在这种情况下，构建了半并行架构，其中每个 DSP48 每个通道处理 K 个系数，其中 K 是时钟速率与复合采样率之间的比率。最有效的实现是将滤波器分为 K 个阶段，每个 DSP48 处理这 K 个阶段的特定系数。

At each clock cycle, the successive phases of the filter output are computed and need to be accumulated together to form an output sample (once every K cycle). Consequently, an additional accumulator is required at the filter output compared with a parallel implementation. This full-precision accumulator works on a large data width, equal to bS+bC+bF, where bS and bC are respectively the bit widths of the data samples and coefficients, and bF=Log2N is the filter bit growth, N being the total number of coefficients. Normal practice is therefore to implement the accumulator within a DSP48 slice to ensure support for the highest clock rate while minimising footprint and power.
在每个时钟周期，都会计算滤波器输出的连续相位，并且需要将其累积在一起以形成输出样本（每 K 个周期一次）。因此，与并行实现相比，滤波器输出端需要一个额外的累加器。该全精度累加器工作在大数据宽度上，等于bS+bC+bF，其中bS和bC分别是数据样本和系数的位宽度，bF=Log2N是滤波器位增长，N是总数系数的数量。因此，通常的做法是在 DSP48 Slice 内实现累加器，以确保支持最高时钟速率，同时最大限度地减少占用空间和功耗。

Figure 2 - Implementation of a semi-parallel filter on 7 Series (above) and UltraScale (below) architectures
图 2 - 在 7 系列（上图）和 UltraScale（下图）架构上实现半并行滤波器

It should be noted that semi-parallel architectures can be derived for any type of filter: single-rate, integer or fractional-rate interpolation and decimation. Figure 2 shows a simplified block diagram for both 7 Series and UltraScale implementations. It clearly highlights the advantage of the UltraScale solution, since the phase accumulator is absorbed by the last DSP48 slice thanks to the W-mux capability.
应该注意的是，可以为任何类型的滤波器导出半并行架构：单速率、整数或分数速率插值和抽取。图 2 显示了 7 系列和 UltraScale 实施的简化框图。它清楚地突出了 UltraScale 解决方案的优势，因为借助 W-mux 功能，相位累加器被最后一个 DSP48 切片吸收。

It is well known that you can rewrite the equation of a complex product to use only three real multiplications. By exploiting the built-in pre-adder, you can implement a complex multiplier with three DSP48s only; one to compute P1 and the other two to handle the PI and PQ outputs. Depending on the latency requirements, which also dictate the speed performance, some logic needs to be added to balance the delays between the different data paths. To get maximal speed support, the DSP48 must be fully pipelined, which results in an overall latency of six cycles for the operator. A two-cycle delay line is consequently added on each input to correctly align the real and imaginary data paths. Those are implemented with four SRL2 per input bit, which are in effect packed into two LUTs by taking advantage of the SRL compression capabilities.
众所周知，您可以重写复数乘积的方程以仅使用三个实数乘法。通过利用内置的预加法器，您只需三个 DSP48 即可实现复杂的乘法器；一个用于计算 P1，另外两个用于处理 PI 和 PQ 输出。根据延迟要求（也决定了速度性能），需要添加一些逻辑来平衡不同数据路径之间的延迟。为了获得最大速度支持，DSP48 必须完全流水线化，这会导致操作员的总体延迟为 6 个周期。因此，在每个输入上添加两个周期延迟线，以正确对齐实部和虚部数据路径。这些是通过每个输入位四个 SRL2 来实现的，它们实际上通过利用 SRL 压缩功能打包到两个 LUT 中。

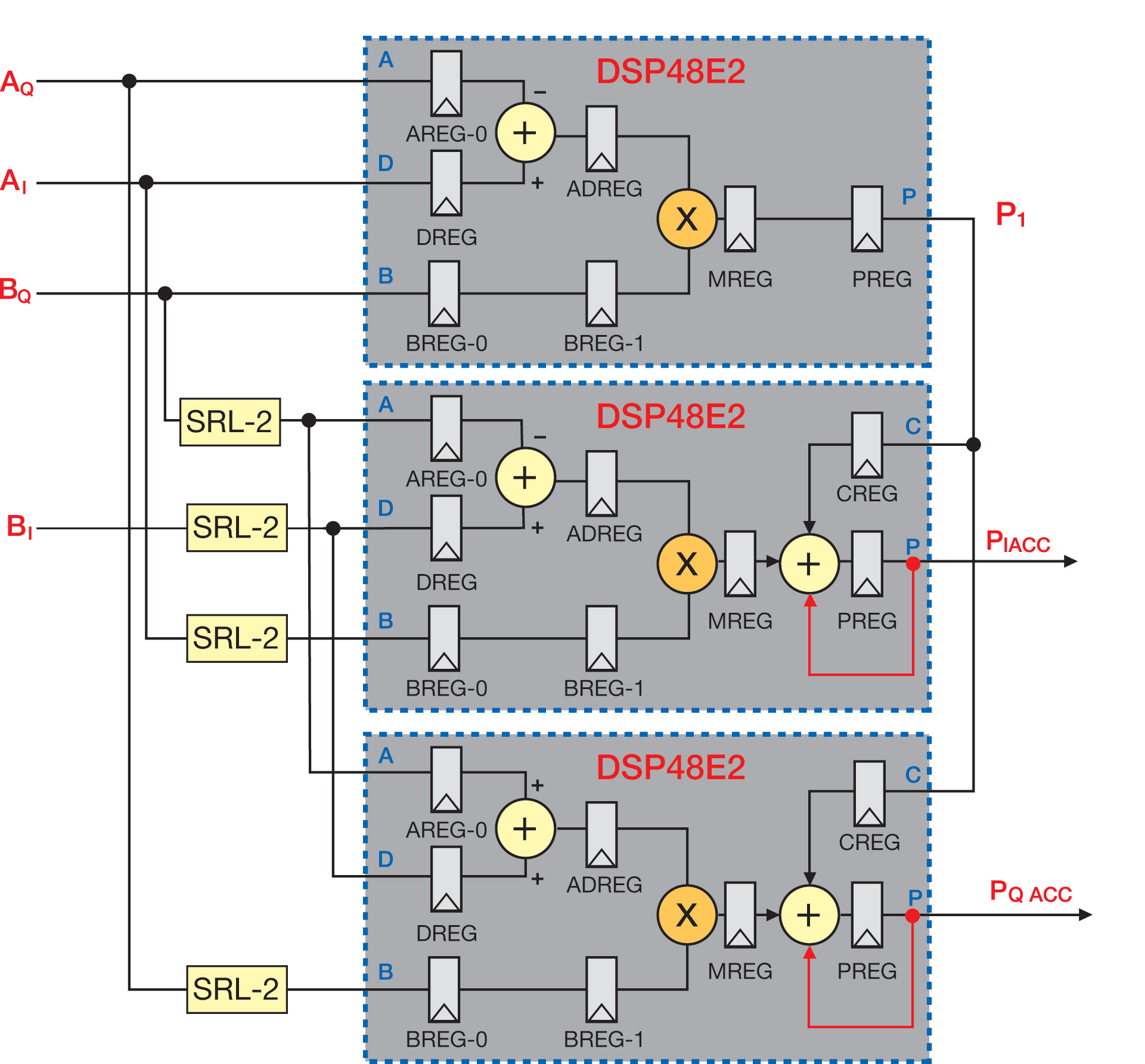
Figure 3 - Implementation of a complex MAC on 7 Series and UltraScale architectures
图 3 - 在 7 系列和 UltraScale 架构上实现复杂 MAC

The complex MAC is finally completed by adding an accumulator on each of the PI and PQ outputs. Again this accumulator works on large data widths and is therefore better integrated within a DSP48 slice. The corresponding implementation for an UltraScale device is shown in Figure 3, which demonstrates the benefit of the W-mux integration. The PI and PQ DSP48E2 slices absorb the accumulators, with 40% resource savings. It is worth mentioning that the latency is also reduced, which may be beneficial for some applications.
最终通过在每个 PI 和 PQ 输出上添加累加器来完成复杂的 MAC。同样，该累加器适用于大数据宽度，因此可以更好地集成在 DSP48 Slice 中。 UltraScale 器件的相应实现如图 3 所示，它展示了 W-mux 集成的优势。 PI 和 PQ DSP48E2 切片吸收了累加器，可节省 40% 的资源。值得一提的是，延迟也减少了，这可能对某些应用程序有利。

Using a similar construction, you can build a complex filter (one with complex data and coefficients) with three real filters, as depicted in Figure 4. The real and imaginary parts of the input signal are fed into two real filters, with coefficients derived respectively as the difference and sum of the imaginary and real parts of the filter coefficients. The third filter processes the sum of the input real and imaginary parts in parallel, using the real part of the coefficients.
使用类似的结构，您可以使用三个实数滤波器构建一个复数滤波器（一个具有复数数据和系数），如图 4 所示。输入信号的实部和虚部被馈送到两个实数滤波器，并分别导出系数作为滤波器系数的虚部和实部的差和和。第三个滤波器使用系数的实部并行处理输入实部和虚部之和。

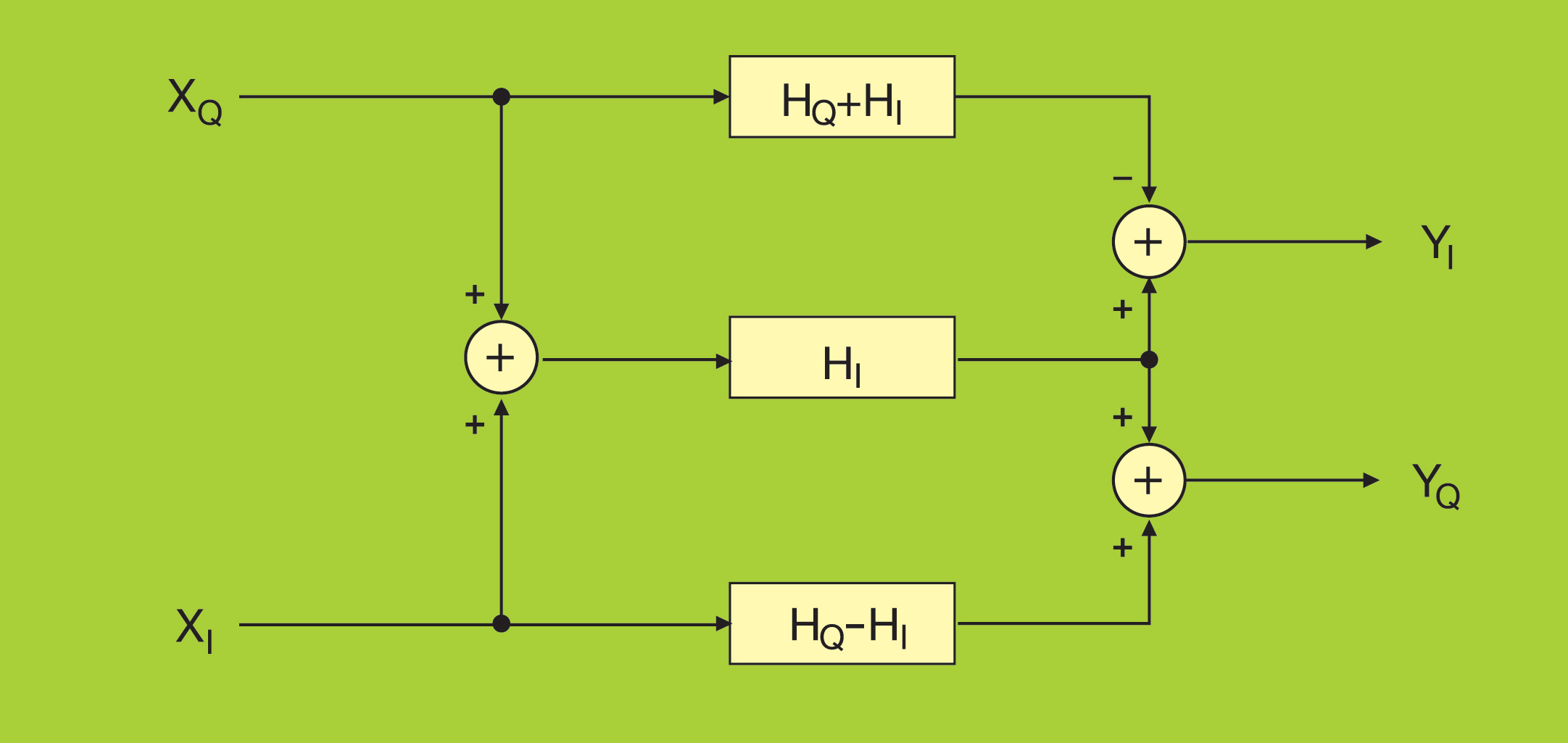
Figure 4 - Implementation architecture of a complex filter
图 4 - 复杂过滤器的实现架构

The outputs of these three filters are finally combined to generate the real and imaginary components of the output, which can again benefit from the W-mux, when parallel filters need to be built, which is typically the case for the equalisers used in DFE applications.
这三个滤波器的输出最终组合起来生成输出的实部和虚部，当需要构建并行滤波器时（DFE 应用中使用的均衡器通常会出现这种情况），这可以再次受益于 W-mux 。

This article was edited from the original by Philip Ling, Editor, Electronic Specifier Design. The original article can be viewed here.
本文由 Electronic Specifier Design 编辑 Philip Ling 编辑。原文可以在这里查看。