Equivalent electromagnetic parameters extraction method for graded honeycomb absorbing materials
分级蜂窝吸波材料的等效电磁参数提取方法

Abstract 摘要

An extraction method for the equivalent electromagnetic parameters (EEP) of grading honeycomb absorbing materials (GHAM) is proposed based on the asymmetric property of GHAM, EEP was modified by gradient factors related to its physical parameters in this paper. Considering that the strength of electromagnetic wave loss is dominated by the imaginary part of the complex dielectric constant, the EEP extraction method is built by optimizing the imaginary part of the complex dielectric constant according to the GHAM’s physical properties, such as the coating thickness of each layer for the GHAM, the increment between two adjacent gradient coatings, the layers of the GHAM, and the total axial height of graded honeycomb. The GHAM were prepared by the immersion process, and the reflectance measured by the free space method was consistent with that calculated by the EEP extraction method proposed in this paper within 2–18 GHz. The proposed EEP extraction method is simple, convenient, high precision, and it has played a certain role in solving the problems in actual engineering applications.
本文基于分级蜂窝吸波材料（GHAM）的非对称特性，提出了一种分级蜂窝吸波材料等效电磁参数（EEP）的提取方法。考虑到电磁波损耗的强度受复介电常数虚部的支配，本文根据 GHAM 的物理特性，如 GHAM 每层涂层厚度、相邻两层梯度涂层之间的增量、GHAM 的层数和梯度蜂窝的总轴向高度，通过优化复介电常数的虚部，建立了 EEP 提取方法。GHAM 是通过浸泡工艺制备的，在 2-18 GHz 范围内，自由空间法测得的反射率与本文提出的 EEP 提取法计算的反射率一致。本文提出的 EEP 提取方法简单、方便、精度高，对解决实际工程应用中的问题起到了一定的作用。

1 Introduction
1 简介

Absorbing materials have recently received more and more extensive attention. Honeycomb materials, owning to light-weight, good strength, low-density, have been studying deeply by researchers [1,2,3]. This material can carry both bearing strength (as a structural component) and absorb waves (effectively reducing the reflection of radar waves), which can be applied to the low observable technology [4,5,6]. We refer to this kind of material that can absorb electromagnetic waves like honeycomb structure as honeycomb absorbing materials (HAM). In general, HAM are prepared by impregnation of aramid paper frame within water solutions of conductive carbon blacks, and thus its absorbing mechanism is mainly dielectric loss or Ohmic loss [7,8,9].
近年来，吸波材料受到越来越广泛的关注。蜂窝材料具有重量轻、强度高、密度低的特点，一直被研究人员深入研究[1,2,3]。这种材料既能承载强度（作为结构部件），又能吸波（有效减少雷达波的反射），可应用于低观测技术[4,5,6] 。我们把这种能像蜂窝结构一样吸收电磁波的材料称为蜂窝吸收材料（HAM）。一般来说，HAM 是将芳纶纸框浸渍在导电碳黑的水溶液中制备而成，因此其吸收机制主要是介电损耗或欧姆损耗[7,8,9] 。

In practical engineering, it is of great concern to know the equivalent electromagnetic parameters (EEP) of the HAM, namely the dielectric constant and the magnetic permeability. There are some works mainly committed to develop methods to extract effective electromagnetic parameters of metamaterials [10,11,12]. Alexander et al. [13] presented an approach to the bianisotropy homogenization of optical metamaterials and discussed several techniques for validating the retrieved effective parameters of these nanostructures. Another method was demonstrated to retrieved the effective parameters for an omega medium and its corresponding CMM by Li et al. [14]. Chen et al. [15] proposed a method to retrieve the effective constitutive parameters of a slab of bianisotropic metamaterial composed of split-ring resonators from the measurement of the S parameters. These works are of great help to the research on the equivalent parameters of the honeycomb. Generally, there are two fundamental theories to model the EEP of HAM: Hashin–Shtrikman (HS) variational theory [16] and strong fluctuation theory [17]. For the HS theory, it first gives the upper and lower bounds of the equivalent parameters of multiphase media materials. For the strong fluctuation theory, it has a more accurate prediction of the equivalent dielectric constant of the dielectric material compared with the weak wave theory (that is, the HS theory). Since then, researchers have done a great quantity of work based on the two fundamental theories. Martin Johansson [18] calculated the HAM using the finite element method and the HS theory, and found that the theoretical upper bound of HS is more suitable for the equivalent parameters of the HAM. F. C. Smith [19] obtained the EEP of the honeycomb by using the finite difference time domain method to calculate the reflection coefficient and transmission coefficient of the honeycomb structure under plane wave irradiation in three mutually orthogonal directions. Zhao [20] established a dispersion-equivalent parameter model of the HAM based on strong fluctuation theory and introducing the dispersion characteristics of HAM. Besides, our team [21] proposed a closed-form representation for EEP of biaxial anisotropic HAM based on long-wavelength approximation. These models have contributed greatly to the design of cellular absorbing materials.
在实际工程中，了解超材料的等效电磁参数（EEP），即介电常数和磁导率，是一个非常重要的问题。有一些研究主要致力于开发提取超材料有效电磁参数的方法 [10,11,12] 。Alexander 等人[13]介绍了光学超材料的各向同性均质化方法，并讨论了验证这些纳米结构有效参数的几种技术。Li 等人[14]展示了另一种方法来检索欧米茄介质及其相应坐标测量机的有效参数。Chen 等人[15]提出了一种通过测量 S 参数来获取由分裂环谐振器组成的双向各向异性超材料板的有效结构参数的方法。这些工作对蜂窝等效参数的研究有很大帮助。一般来说，有两种基本理论来模拟 HAM 的 EEP：Hashin-Shtrikman（HS）变分法理论 [16] 和强波动理论 [17] 。对于 HS 理论，它首先给出了多相介质材料等效参数的上下限。对于强波动理论，与弱波理论（即 HS 理论）相比，它对介质材料的等效介电常数有更准确的预测。此后，研究人员基于这两种基本理论开展了大量工作。 Martin Johansson [18]利用有限元方法和 HS 理论计算了蜂窝状结构的等效参数，发现 HS 的理论上限更适合于蜂窝状结构的等效参数。F. C. Smith [19] 利用有限差分时域法计算了蜂窝结构在三个相互正交方向的平面波照射下的反射系数和透射系数，得到了蜂窝的 EEP。Zhao [20]以强波动理论为基础，介绍了HAM的色散特性，建立了HAM的色散等效参数模型。此外，我们的团队[21]基于长波长近似，提出了双轴各向异性 HAM EEP 的闭式表示。这些模型极大地促进了蜂窝吸波材料的设计。

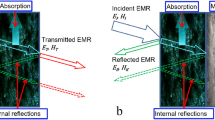
To further improve the absorbing properties of HAM, the researchers designed the grading honeycomb absorbing materials (GHAM) based on the principle of impedance matching [22, 23]. The GHAM is also composed of periodic structural elements, top and side views as shown in Fig. 1a, b, respectively. As can be seen, the gradient honeycomb absorbing material consists of three materials, a honeycomb substrate (Material 1 in Fig. 1b), an absorbing coating coated on the honeycomb substrate (Material 2 in Fig. 1b), and air (Material 3 in Fig. 1b). Compared to HAM, the most important feature of the GHAM is that its absorbing coating is in the form of a gradient. This gradient coating design produces a gradient of impedance that reduces the reflection of electromagnetic waves, thereby enhancing absorbing performance. The number of specific gradient layers N depends on the actual application requirements. In this paper, we discussed the case where each layer of the gradient has the same height and the gradient coating increment is also fixed.
为了进一步提高 HAM 的吸波性能，研究人员根据阻抗匹配原理设计了分级蜂窝吸波材料 (GHAM)[22, 23] 。GHAM 也是由周期性结构元素组成，俯视图和侧视图分别如图 1a 和 b 所示。可以看出，梯度蜂窝吸波材料由三种材料组成，即蜂窝基板（图 1b 中的材料 1）、涂在蜂窝基板上的吸波涂层（图 1b 中的材料 2）和空气（图 1b 中的材料 3）。与 HAM 相比，GHAM 的最大特点是其吸收涂层呈梯度状。这种梯度涂层设计可产生阻抗梯度，减少电磁波的反射，从而提高吸收性能。具体梯度层数 N 取决于实际应用要求。本文讨论的是每层梯度高度相同且梯度涂层增量固定的情况。

Fig. 1 图 1

Schematic views of the unit cell for the GHAM. a The top view schematic of GHAM. b The side view schematic of GHAM
GHAM 的单元格示意图。a GHAM 的俯视示意图。b GHAM 的侧视示意图

Since the absorbing properties of GHAM are far superior to those of homogeneous HAM, GHAM have a wider range of applications. However, there is currently no way to directly calculate or invert the EEP of a gradient honeycomb. The Nicolson–Ross–Weir (NRW) inversion method [24, 25] is a classical method for inverting the electromagnetic parameters of materials by the characteristic impedance Z and the refractive index n. It is worth noting that there are some branch problems about NRW method, such as half-wave resonance, phase angle jump, and multivalued problems. Some researchers also put forward solutions to these problems. For example, for half-wave resonance problems, Baker-Jarvis, Vanzura, and Kissick gave their methods [26], that is imaginary phase compensation method for phase difference problem [27]. In this paper, the equivalent electromagnetic parameter extraction method of the GHAM is proposed based on the NRW method modified by gradient factors related to its physical parameters. The method first obtains the scattering parameters by treating the gradient honeycomb absorbing material as a black box. The preliminary EEP are then obtained by calculation of the scattering parameters. Finally, because the strength of electromagnetic wave loss is mainly affected by the size of the imaginary part of the complex dielectric constant, we optimize the imaginary part of the complex dielectric constant by introducing physical size parameters to obtain the modified EEP. The physical gradient dimensions include the coating thickness of electromagnetic wave incident end, the coating thickness of electromagnetic leaving end, increment between adjacent gradient coatings, the number of gradient layers, and the total axial height of graded honeycomb. The proposed extraction method can calculate the EEP of GHAM accurately, and has the advantages of simple principle, convenient use, high precision and broad bandwidth. It is important for the research of GHAM in the future.
由于 GHAM 的吸收特性远远优于均质 HAM，因此 GHAM 的应用范围更广。然而，目前还没有直接计算或反演梯度蜂窝的 EEP 的方法。Nicolson-Ross-Weir (NRW) 反演法[24, 25] 是通过特性阻抗 Z 和折射率 n 反演材料电磁参数的经典方法。值得注意的是，NRW 方法存在一些分支问题，如半波共振、相角跳跃和多值问题。一些研究人员也提出了解决这些问题的方法。例如，对于半波共振问题，Baker-Jarvis、Vanzura 和 Kissick 提出了他们的方法 [26]，即相位差问题的虚相补偿方法 [27]。本文在 NRW 方法的基础上，提出了 GHAM 的等效电磁参数提取方法，并对其物理参数相关梯度因子进行了修正。该方法首先将梯度蜂窝吸波材料视为黑箱，从而获得散射参数。然后通过计算散射参数获得初步的 EEP。最后，由于电磁波损耗强度主要受复介电常数虚部大小的影响，我们通过引入物理尺寸参数来优化复介电常数的虚部，从而得到修正的 EEP。 物理梯度尺寸包括电磁波入射端的涂层厚度、电磁波出射端的涂层厚度、相邻梯度涂层之间的增量、梯度层数以及梯度蜂窝的总轴向高度。所提出的提取方法能精确计算 GHAM 的 EEP，具有原理简单、使用方便、精度高、带宽宽等优点。它对未来 GHAM 的研究具有重要意义。

2 EEP extraction method for a GHAM
2 GHAM的EEP提取方法

In this paper, the preliminary EEP of HAM were first obtained by using the NRW method and the imaginary phase compensation method, regardless of the limitations of the NRW method. Afterwards, for the unique structure of the gradient honeycomb, we obtained the modified EEP of the GHAM by modifying the preliminary EEP.
在本文中，我们不考虑 NRW 方法的局限性，首先利用 NRW 方法和虚相补偿方法得到了 HAM 的初步 EEP。之后，针对梯度蜂窝的独特结构，我们通过修改初步 EEP 得到了 GHAM 的修正 EEP。

According to NRW retrieval method [24, 25] and the transmission line theory [28], the equivalent magnetic permeability and equivalent permittivity of the material can be determined as:
根据 NRW 检索方法 [24, 25] 和传输线理论 [28] ，可以求出材料的等效磁导率和等效介电常数：

$$n={\cos }^{-1}\left(\frac{1-s_{11}^2+s_{21}^2}{2s_{21}}\right)/\phantom{\left(\frac{1-s_{11}^2+s_{21}^2}{2s_{21}}\right)kd}kd,$$

(1)

$$Z_{\text{s}}^{{}^{\mathrm{\prime }}}=\sqrt{\left[{\left(1+s_{11}\right)}^2-s_{21}^2\right]/\phantom{\left[{\left(1+s_{11}\right)}^2-s_{21}^2\right]\left[{\left(1-s_{11}\right)}^2-s_{21}^2\right]}\left[{\left(1-s_{11}\right)}^2-s_{21}^2\right]},$$

(2)

$${\mu }_{\text{r}}=Z_{\text{S}}^{\mathrm{\prime }}n,$$

(3)

$${\text{ε}}_{\text{r}}=n/Z_{\text{S}}^{\mathrm{\prime }},$$

(4)

where n is the refractive index of the material used to construct the sample and $Z_{\text{s}}^{{}^{\mathrm{\prime }}}$ is the impedance of the sample (relative permittivity, ${\text{ε}}_{\text{r}}$; relative permeability, ${\mu }_{\text{r}}$), Where d is the thickness of the material, k is the free space wave number, and $S_{11}$,$S_{21}\text{and}{S}_{22}$ are the scattering parameters.
其中 n 是构建样品所用材料的折射率， $Z_{\text{s}}^{{}^{\mathrm{\prime }}}$ 是样品的阻抗（相对介电常数， ${\text{ε}}_{\text{r}}$ ；相对磁导率， ${\mu }_{\text{r}}$ ），其中 d 是材料的厚度、k 为自由空间波数， $S_{11}$ , $S_{21}\text{and}{S}_{22}$ 为散射参数。

Due to the phase difference, it is difficult to determine the phase when calculating. The imaginary phase compensation method [27] can solve this problem. We call the EEP obtained by the compensation method as the preliminary EEP. It can also be expressed as
由于存在相位差，计算时很难确定相位。虚相位补偿法 [27] 可以解决这个问题。我们将补偿方法得到的 EEP 称为初步 EEP。它也可以表示为

$${\mu }_{\text{r}}={\mu }^{\mathrm{\prime }}-j{\mu }^{\mathrm{\prime }\mathrm{\prime }},$$

(5)

$${\text{ε}}_{\text{r}}={\text{ε}}^{\mathrm{\prime }}-j{\text{ε}}^{\mathrm{\prime }\mathrm{\prime }}.$$

(6)

The preliminary equivalent parameters given above are obtained by using the reflection and transmission coefficients of electromagnetic waves incident on the structure. The NRW method is generally suitable for materials with uniform and moderate thickness. For GHAM, this approach does not take into account the unique physical property of the gradient honeycomb material.
上述初步等效参数是利用入射到结构上的电磁波的反射系数和透射系数得到的。NRW 方法一般适用于厚度均匀适中的材料。对于 GHAM，这种方法没有考虑到梯度蜂窝材料的独特物理特性。

In practical engineering, it is of great concern to know the EEP of the honeycomb absorbing materials, including GHAM. And in the process of calculated the EEP of the GHAM, we found that the traditional research methods such as Nicolson–Ross–Weir is no longer suitable considered that the GHAM is not symmetry, that is S₁₁ ≠ S₂₂ [29]. When we initially performed the simulated calculation for GHAM, we found that S₁₁ is not equal to S₂₂, which can be seen in Fig. 2. To solve this problem, we proposed a new modification method. For the purpose of calculation facilitating, we used the hierarchical cascade methods for the GHAM.
在实际工程中，了解包括 GHAM 在内的蜂窝吸波材料的 EEP 非常重要。而在计算 GHAM 的 EEP 的过程中，我们发现传统的研究方法，如 Nicolson-Ross-Weir 已不再适用，因为 GHAM 并非对称、即 S₁₁≠ S₂₂ [29] 。我们最初对 GHAM 进行模拟计算时，发现 S₁₁ 不等于 S₂₂ ，这可以从图 2 中看出。为了解决这个问题，我们提出了一种新的修改方法。为了便于计算，我们对 GHAM 采用了分层级联方法。

Fig. 2 图 2

Scattering coefficients of the GHAM. a Real part of scattering coefficients S₁₁ and S₂₂ of GHAM for simulation. b Imaginary part of scattering coefficients S₁₁ and S₂₂ of GHAM
GHAM 的散射系数。a 模拟 GHAM 的散射系数 S₁₁ 和 S₂₂ 的实部。b GHAM 的 S₁₁ 和 S₂₂ 散射系数的虚部。

Gradient honeycomb absorbing material are all non-magnetic materials, and the absorption of electromagnetic waves is mainly related to the dielectric constant. The dielectric constant is a complex number, the real part represents the permittivity, and the imaginary part mainly represents the loss. Changing the real part will result in the movement of the absorption peak, while changes in the imaginary part will have an effect on the absorption amplitude. Generally, as long as the simulated reflectivity is consistent with the calculated reflectivity by EEP, the EEP is considered to be correct. So the motivation of the proposed modification is based on the comparison of reflectivity. Considering that the EEP are affected by the coating thickness, material height and other size parameters. Therefore, it is necessary to modify the imaginary part.
梯度蜂窝吸波材料都是非磁性材料，对电磁波的吸收主要与介电常数有关。介电常数是一个复数，实部代表介电常数，虚部主要代表损耗。实部的变化会导致吸收峰的移动，而虚部的变化则会对吸收振幅产生影响。一般来说，只要模拟的反射率与 EEP 计算的反射率一致，就可以认为 EEP 是正确的。因此，建议修改的动机就是基于反射率的比较。考虑到 EEP 受涂层厚度、材料高度和其他尺寸参数的影响。因此，有必要修改虚部。

After the above analysis, the imaginary part of the dielectric constant of the GHAM is modified as follows:
经过上述分析，GHAM 介电常数的虚部修正如下：

$${\text{ε}}_{\text{e}}^{\mathrm{\prime }\mathrm{\prime }}={\text{ε}}^{\mathrm{\prime }\mathrm{\prime }}\cdot \exp \left\{\left(1+\frac{t_{\text{out}}}{t_{\text{in}}}\cdot \frac{1}{p}\right)\left(\frac{t_{\text{in}}-t_{\text{out}}}{\mathrm{\Delta }t}\right)\left|\frac{1}{f\sqrt{{\mu }_0{\text{ε}}_0}}-h\right|\right\},$$

(7)

where $t_{\mathrm{i}\mathrm{n}}$ ($t_{\mathrm{i}\mathrm{n}}=t_1$) is the coating thickness of the first arrival layer of the incident wave, $t_{\mathrm{o}\mathrm{u}\mathrm{t}}$ ($t_{\mathrm{o}\mathrm{u}\mathrm{t}}=t_n$) is the coating thickness of the finally arrival layer of incidence wave, $\mathrm{\Delta }t$ is the increment between adjacent gradient coatings, p is the number of gradient layers, h is the total axial height of graded honeycomb, f is the working frequency. Therefore, ${\text{ε}}_{\text{e}}^{{}^{\mathrm{\prime }\mathrm{\prime }}}$ is the modified imaginary part of the dielectric constant of the GHAM.
其中 $t_{\mathrm{i}\mathrm{n}}$ ( $t_{\mathrm{i}\mathrm{n}}=t_1$ ) 是入射波第一到达层的涂层厚度、 $t_{\mathrm{o}\mathrm{u}\mathrm{t}}$ ( $t_{\mathrm{o}\mathrm{u}\mathrm{t}}=t_n$ )是入射波最后到达层的涂层厚度、 $\mathrm{\Delta }t$ 是相邻梯度涂层之间的增量，p 是梯度层数，h 是梯度蜂窝的总轴向高度，f 是工作频率。因此， ${\text{ε}}_{\text{e}}^{{}^{\mathrm{\prime }\mathrm{\prime }}}$ 是 GHAM 介电常数的修正虚部。

Where $\left|\frac{1}{f\sqrt{{\mu }_0{\text{ε}}_0}}-h\right|$ is a correction factor for the height of the honeycomb, which represents the EEP deviation from the height of the honeycomb. Besides, the gradation of the GHAM may be positive or negative according to the incidence direction of the electromagnetic wave, and the difference in the number of layers and the coating increment will also affect the EEP, so $\left(1+t_{\text{out}}/\phantom{t_{\text{out}}p{t}_{\text{in}}}p{t}_{\text{in}}\right)\left[\left(t_{\text{in}}-t_{\text{out}}\right)/\phantom{\left(t_{\text{in}}-t_{\text{out}}\right)\mathrm{\Delta }t}\mathrm{\Delta }t\right]$ is the coating correction factor.
其中 $\left|\frac{1}{f\sqrt{{\mu }_0{\text{ε}}_0}}-h\right|$ 是蜂窝高度的修正系数，表示 EEP 与蜂窝高度的偏差。此外，根据电磁波的入射方向，GHAM 的分级可能是正的，也可能是负的，层数和涂层增量的差异也会影响 EEP，因此 $\left(1+t_{\text{out}}/\phantom{t_{\text{out}}p{t}_{\text{in}}}p{t}_{\text{in}}\right)\left[\left(t_{\text{in}}-t_{\text{out}}\right)/\phantom{\left(t_{\text{in}}-t_{\text{out}}\right)\mathrm{\Delta }t}\mathrm{\Delta }t\right]$ 是涂层修正系数。

Substituting Eq. (7) into (5) and (6), the modified EEP for the GHAM can be obtained. That is,
将公式（7）代入（5）和（6），即可得到 GHAM 的修正 EEP。即

$${\mu }_{\text{e}}={\mu }^{\mathrm{\prime }}-j{\mu }^{\mathrm{\prime }\mathrm{\prime }},$$

(8)

$${\text{ε}}_{\text{e}}={\text{ε}}^{\mathrm{\prime }}-j{\text{ε}}_{\text{e}}^{\mathrm{\prime }\mathrm{\prime }}.$$

(9)

So far, the modified EEP for the GHAM have been built, and their reliability will be verified by an example in the next chapter.
到目前为止，针对 GHAM 的改进型 EEP 已经完成，其可靠性将在下一章的示例中得到验证。

3 Reliability verification of the proposed equivalent electromagnetic parameters method
3 拟议等效电磁参数法的可靠性验证

3.1 Numerical simulation verification
3.1 数值模拟验证

Based on the above method, we can obtain the EEP of a gradient honeycomb absorber. To verify the reliability of this method, we calculated the EEP of a practical three-layer gradient honeycomb absorber. In the following discussion, the GHAM with three-layer gradient will be considered for the sake of simplicity.
根据上述方法，我们可以得到梯度蜂窝吸收器的 EEP。为了验证这种方法的可靠性，我们计算了一个实用的三层梯度蜂窝吸波材料的 EEP。为简单起见，下文将讨论三层梯度 GHAM。

The scattering coefficients ($S_{11}$ and $S_{21}$) of the GHAM are obtained based on commercial simulation software—CST Microwave Studio. In the numerical simulation, the periodic cell dimensions of the honeycomb structure and the coordinate axis orientation are selected exactly as shown in Fig. 1a, b. Correspondingly, the unit cell boundary condition in the x–y directions and the Floquet ports in the z-direction are used in CST Microwave Studio.
GHAM 的散射系数（ $S_{11}$ 和 $S_{21}$ ）是基于商业仿真软件--CST Microwave Studio 得出的。在数值模拟中，蜂窝结构的周期单元尺寸和坐标轴方向的选择如图1a、b所示。相应地，在 CST Microwave Studio 中使用了 x-y 方向的单元单元边界条件和 z 方向的 Floquet 端口。

The electromagnetic wave is incident in the direction of the positive gradient of the gradient honeycomb absorbing material. The substrate material (that is, material 1 in Fig. 1b) of the honeycomb structure is an aramid paper (To be consistent with the experiment to be introduced next) with the electromagnetic parameters of ${\text{ε}}_1$=1.6 and ${\mu }_1$=1. Other key dimensions include the wall thickness W = 0.1 mm and the aperture side-length r = 1.83 mm. The absorbing coating (that is, material 2 in Fig. 1b) utilized by the honeycomb absorbing structure is still fabricated in our lab, and its relative permittivity are the same as that in Fig. 5 in [21]. The relative permeability ${\mu }_2$ is set 1 considering of its non-magnetic. The gradient coating thicknesses are $t_1$=12.5 μm, $t_2$=25 μm, $t_3$=37.5 μm, and the gradient coating height corresponding to this is $h_1$=$h_2$=$h_3$=6.67 mm, respectively. The material 3 is set to air.
电磁波沿梯度蜂窝吸波材料的正梯度方向入射。蜂窝结构的基底材料（即图1b中的材料1）是芳纶纸（为了与接下来介绍的实验保持一致），其电磁参数为 ${\text{ε}}_1$ =1.6 和 ${\mu }_1$ =1.其他关键尺寸包括壁厚 W=0.1 毫米和孔边长 r=1.83 毫米。蜂窝吸波结构所使用的吸波涂层（即图 1b 中的材料 2）仍由本实验室制造，其相对介电常数与 [21] 中的图 5 相同。考虑到其非磁性，相对磁导率 ${\mu }_2$ 设置为 1。梯度涂层厚度分别为： $t_1$ =12.5 μm、 $t_2$ =25 μm、 $t_3$ =37.5 μm，与此相对应的梯度涂层高度分别为 $h_1$ = $h_2$ = $h_3$ =6.67 mm。材料 3 设置为空气。

Then the scattering coefficients of ${\mathrm{S}}_{11}$ and ${\mathrm{S}}_{21}$ can be obtained by simulated results, as shown in Fig. 3a, b. Next, bring the scattering parameters into Formula (3)–(15) and solving the multi-valued problem, the preliminary equivalent permeability and the preliminary equivalent permittivity of the medium are obtained, as shown in Fig. 4a, b.
然后通过模拟结果可以得到 ${\mathrm{S}}_{11}$ 和 ${\mathrm{S}}_{21}$ 的散射系数，如图 3a, b 所示。接下来，将散射参数带入式（3 ）-（15 ），求解多值问题，即可得到介质的初步等效渗透率和初步等效介电常数，如图4a, b所示。

Fig. 3 图 3

Scattering coefficients S₁₁ and S₂₁ of the GHAM. a The real part of scattering coefficients of GHAM. b The imaginary part of scattering coefficients of GHAM
GHAM 的散射系数 S₁₁ 和 S₂₁ 。a GHAM 的散射系数实部。b GHAM 的散射系数的虚部。

Fig. 4 图 4

EEP of the GHAM. a The real part of EEP of the GHAM. b The imaginary part of EEP of the GHAM
GHAM 的 EEP。a GHAM 的 EEP 实部。b GHAM 的 EEP 虚部

As can be seen, Fig. 4a shows the real part of the preliminary equivalent constant dielectric constant (${\text{ε}}^{\mathrm{\prime }}$) and the real part of the preliminary equivalent permeability (${\mu }^{\mathrm{\prime }}$), and Fig. 4b shows the imaginary part of the preliminary equivalent dielectric constant (${\text{ε}}^{\mathrm{\prime }\mathrm{\prime }}$) and imaginary part of the preliminary equivalent magnetic permeability (${\mu }^{\mathrm{\prime }\mathrm{\prime }}$). At the same time, the ${\text{ε}}_{\text{e}}^{{}^{\mathrm{\prime }\mathrm{\prime }}}$ of GHAM is obtained based on Eq. (7) just as shown in Fig. 4b. It can be seen that the imaginary part of the dielectric constant after the correction is different from that before the correction across the entire 2–18 GHz range. And the imaginary part of the dielectric constant after the correction is significantly smaller than that before the correction.
可以看出，图 4a 显示了初步等效常数介电常数的实部（ ${\text{ε}}^{\mathrm{\prime }}$ ）和初步等效磁导率的实部（ ${\mu }^{\mathrm{\prime }}$ ），图 4b 显示了初步等效介电常数的虚部（ ）。4b 显示了初步等效介电常数的虚部（ ${\text{ε}}^{\mathrm{\prime }\mathrm{\prime }}$ ）和初步等效磁导率的虚部（ ${\mu }^{\mathrm{\prime }\mathrm{\prime }}$ ）。同时，根据公式（7）得到 GHAM 的 ${\text{ε}}_{\text{e}}^{{}^{\mathrm{\prime }\mathrm{\prime }}}$ 如图 4b 所示。可以看出，在整个 2-18 GHz 范围内，校正后介电常数的虚部与校正前不同。修正后介电常数的虚部明显小于修正前。

In order to prove the correctness of the modified EEP, we compared the reflectivity simulated by CST software with the reflectivity calculated by the modified EEP and the reflectivity calculated by the preliminary EEP. In the first, the reflectivity of the honeycomb absorbing structure is calculated based on the EEP method proposed by [30]. Then, we used the CST software to simulate the reflectivity of the honeycomb absorbing structure with the same parameters.
为了证明修正 EEP 的正确性，我们将 CST 软件模拟的反射率与修正 EEP 计算的反射率和初步 EEP 计算的反射率进行了比较。首先，根据 [30] 提出的 EEP 方法计算蜂窝吸波结构的反射率。然后，我们使用 CST 软件以相同的参数模拟蜂窝吸波结构的反射率。

The reflectance comparison of the three cases is proposed as shown in Fig. 5. It can be seen from Fig. 5 that the reflectance calculated using the modified EEP deduced in this paper is consistent with the simulation within 2–18 GHz. However, the reflectance calculated using the preliminary EEP is very different from the simulated reflectance, especially in the low-frequency region of 2–6 GHz. Therefore, it can be proved that the modified equivalent electromagnetic parameter extraction model of GHAM is reliable. This illustrates that this work is effective, and it has played a certain role in solving the problems in actual engineering applications.
三种情况的反射率比较如图5所示。从图5中可以看出，使用本文推导出的修正 EEP 计算出的反射率在 2-18 GHz 范围内与模拟一致。然而，使用初步 EEP 计算出的反射率与模拟反射率相差很大，尤其是在 2-6 GHz 的低频区域。因此，可以证明 GHAM 的修正等效电磁参数提取模型是可靠的。这说明这项工作是有效的，对解决实际工程应用中的问题起到了一定的作用。

Fig. 5 图 5

Reflectance comparison of the three cases including calculation by the preliminary EEP, simulation by CST and calculation by the modified EEP
三种情况的反射率比较，包括初步 EEP 计算、CST 模拟和修改后的 EEP 计算

In addition, we also verified the GHAM with four-layer gradient and GHAM with five-layer gradient, the result shows that it is feasible. The modification may be affected by the height of sample, so the actual sample should not be too high. It is also necessary to ensure that the periodic structure size of the material is much smaller than the wavelength, so as to avoid the error caused by simulation. However, as long as the parameters are within a reasonable range, it has certain application value in practical engineering.
此外，我们还验证了四层梯度的 GHAM 和五层梯度的 GHAM，结果表明是可行的。改性可能会受到样品高度的影响，因此实际样品不宜过高。此外，还需要确保材料的周期结构尺寸远小于波长，以避免模拟造成的误差。不过，只要参数在合理范围内，在实际工程中还是有一定应用价值的。

3.2 Experimental verification
3.2实验验证

To further verify the correctness of the modified EEP of the GHAM proposed in this paper, the experimental verification is carried out. By preparing a GHAM, the reflectivity is tested and compared with the reflectance calculated from the modified EEP and simulation by CST.
为了进一步验证本文提出的 GHAM 修正 EEP 的正确性，我们进行了实验验证。通过制备 GHAM，测试其反射率，并将其与根据修改后的 EEP 和 CST 仿真计算出的反射率进行比较。

The honeycomb absorbing structure is fabricated by an impregnation process in our lab [21], the dimension of the measured sample is 200 × 200 mm², as shown in Fig. 6. To obtain a honeycomb wave absorbing material with a gradient coating, we cut a 20 mm honeycomb into three layers at equal height and then impregnated different coating thicknesses. The sample images are shown in Fig. 6a–c, is the aperture micrograph of the 3-layer gradient honeycomb sample. The electromagnetic parameters of the material used to construct the GHAM sample are consistent with the simulation and calculation in the previous section.
蜂窝状吸波结构是我们实验室采用浸渍工艺[21]制作的，实测样品尺寸为 200 × 200 mm²，如图6所示。为了获得具有梯度涂层的蜂窝吸波材料，我们将 20 毫米的蜂窝切割成等高的三层，然后浸渍不同厚度的涂层。样品图像如图6-c所示，是三层梯度蜂窝样品的孔径显微照片。用于构建 GHAM 样品的材料的电磁参数与上一节的模拟和计算结果一致。

Fig. 6 图 6

Photograph of the fabricated honeycomb absorbing structure. a The sample of the GHAM. c The zoom part of the GHAM. b The image of the GHAM
制造的蜂窝吸波结构照片。a GHAM 样品。c GHAM 的放大部分。b GHAM 的图像

The reflectance is measured using the arched frame test method [31,32,33,34,35,36]. The reflectance comparison of the three cases is proposed as shown in Fig. 7. It can be seen from Fig. 7 that the reflectance calculated using EEP deduced in this paper is consistent with the measurement and the simulation within 2–18 GHz, with only slight deviations at higher frequencies due to fabrication tolerances and imperfect measurements. After the honeycomb material is impregnated with the absorbing paint, it needs to be dried. Due to thermal expansion and contraction, the honeycomb absorbing material will undergo slight deformation after drying, resulting in that the three-layer honeycomb cannot be perfectly aligned with the honeycomb holes. This is also the cause of slight deviations in measured and simulated and calculated reflectance.
反射率的测量采用拱形框架测试法 [31,32,33,34,35,36] 。三种情况的反射率比较如图7所示。从图7中可以看出，本文推导出的使用 EEP 计算出的反射率在 2-18 GHz 范围内与测量值和模拟值一致，仅在较高频率下由于制造公差和不完善的测量值而略有偏差。蜂窝材料浸渍吸波涂料后需要干燥。由于热胀冷缩，蜂窝吸波材料在干燥后会发生轻微变形，导致三层蜂窝无法与蜂窝孔完全对齐。这也是导致测量值与模拟和计算的反射率略有偏差的原因。

Fig. 7 图 7

Reflectance comparison of the three cases including measurement, simulation and calculation
三种情况下的反射率对比，包括测量、模拟和计算

4 Conclusion
4 结论

To summarize, the extraction method of the EEP of GHAM is deduced and verified. Based on the NRW retrieval method, the modified method considering the influences of the gradient structure parameters is built, because the strength of electromagnetic wave loss is mainly affected by the size of the imaginary part of the complex dielectric constant, we optimize the imaginary part of the complex dielectric constant by using physical dimensions, such as the coating thickness of electromagnetic wave incident end, the coating thickness of electromagnetic leaving end, increment between adjacent gradient coatings, the number of gradient layers, and the total axial height of graded honeycomb. The GHAM was prepared by the immersion process, and the reflectance measured by the free space method was consistent with the reflectance calculated by the closed-form representation proposed in this paper within 2–18 GHz. The proposed extraction method can calculate the EEP of GHAM quickly, conveniently and accurately, which is very important for engineering application research of the GHAM.
综上所述，推导并验证了 GHAM 的 EEP 提取方法。由于电磁波损耗的强弱主要受复介电常数虚部大小的影响，我们利用电磁波入射端涂层厚度、电磁波出射端涂层厚度、相邻梯度涂层之间的增量、梯度层数、梯度蜂窝的总轴向高度等物理尺寸优化了复介电常数的虚部。通过浸泡工艺制备了 GHAM，在 2-18 GHz 范围内，自由空间法测得的反射率与本文提出的闭式表示法计算的反射率一致。本文提出的提取方法可以快速、方便、准确地计算出 GHAM 的 EEP 值，对 GHAM 的工程应用研究具有重要意义。