投资组合理论（II）——风险平价策略

[原文是本人在公众号的文章，陆续更新到知乎，并对一些地方进行更新和删减]

关键词：风险平价策略，全天候基金，分散化持仓

风险平价策略

今天我们来聊一聊大名鼎鼎的桥水全天候基金的风险平价策略。

风险平价策略是在分散化持仓的思想下发展出的产物，彼时正是60/40兴盛的年代，但进入千禧年之后60/40的弊病逐渐显现，包括对债务货币化的不适应，和过高的股票市场配置带来的风险占比过大，例如在几个主要的成熟市场里债券和股票的年化波动大概是5%和15%，相关系数<=0.2，那么60/40的总风险中来自股票和债券的比例分别是92%和8%，显然的，波动率过于受某一方的影响是件糟糕的事。

如何计算一种投资组合，使得其中各类波动率资产对总组合的波动率贡献保持均衡？桥水基金在90年代推出的划时代意义的全天候基金（All Weather Fund）提供了思路，它的思想是，既然经济运转会经历美林四象限，在不同的阶段都会有利好的资产，和不利的资产，例如通胀时利好大宗，高增长时利好股票和成长赛道，于是我们可以寻找所有值得投资的标的，构建一个投资组合，再让各资产在调仓周期内对总组合的波动率的贡献保持均等。

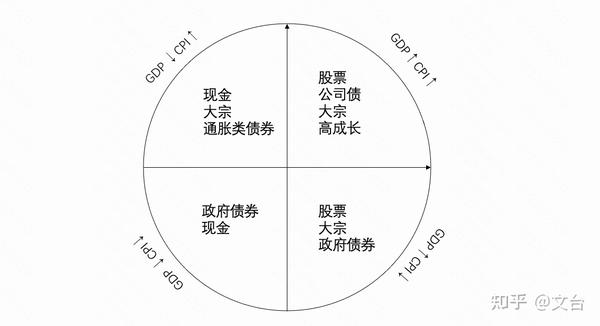
如何定义风险呢？这是个很复杂的问题，常见的有标准差，最大回撤，流动性，甚至政策风险，地域风险，等等都能在某种程度衡量风险，不过这里我们仍采用标准差以求简明。

假设债券和股票的年波动率分别为 ${\sigma }_1$\sigma_{1} 和 ${\sigma }_2$\sigma_{2} ，占有持仓比重 ${\omega }_0$\omega_{0} 和 ${\omega }_1$\omega_{1} ，显然持仓组合的波动率是

$\sigma =\sqrt{({\omega }_0{\sigma }_0{)}^2+({\omega }_1{\sigma }_1{)}^2+2{\rho }_{1,2}{\omega }_0{\omega }_1{\sigma }_0{\sigma }_1}$\sigma=\sqrt{(\omega_{0}\sigma_{0})^{2}+(\omega_{1}\sigma_{1})^{2}+2\rho_{1,2}\omega_{0}\omega_{1}\sigma_{0}\sigma_{1}}

如果股票和债券完全不相关则 ${\rho }_{1,2}=0$\rho_{1,2}=0 ，但真实情况并非如此，交叉项不能被简单省略，那么如何分配交叉项的风险呢，风险平价采用的方法是“等分”，即投资组合内的资产平摊交叉项风险。根据这个思路易知债券和股票各自的风险占组合风险的比例为

$p_0=\frac{({\omega }_0{\sigma }_0{)}^2+{\rho }_{1,2}{\omega }_0{\omega }_1{\sigma }_0{\sigma }_1}{{\sigma }^2}=\frac{{\omega }_0}{\sigma }\frac{\mathrm{\partial }\sigma }{\mathrm{\partial }{\omega }_0}$p_{0}=\frac{(\omega_{0}\sigma_{0})^{2}+\rho_{1,2}\omega_{0}\omega_{1}\sigma_{0}\sigma_{1}}{\sigma^{2}}=\frac{\omega_{0}}{\sigma}\frac{\partial\sigma}{\partial\omega_{0}}
$p_1=\frac{({\omega }_1{\sigma }_1{)}^2+{\rho }_{1,2}{\omega }_0{\omega }_1{\sigma }_0{\sigma }_1}{{\sigma }^2}=\frac{{\omega }_1}{\sigma }\frac{\mathrm{\partial }\sigma }{\mathrm{\partial }{\omega }_1}$p_{1}=\frac{(\omega_{1}\sigma_{1})^{2}+\rho_{1,2}\omega_{0}\omega_{1}\sigma_{0}\sigma_{1}}{\sigma^{2}}=\frac{\omega_{1}}{\sigma}\frac{\partial\sigma}{\partial\omega_{1}}
$p_0+p_1=1$p_{0}+p_{1}=1

其中， $\frac{\mathrm{\partial }\sigma }{\mathrm{\partial }{\omega }_0}$\frac{\partial\sigma}{\partial\omega_{0}} 和 $\frac{\mathrm{\partial }\sigma }{\mathrm{\partial }{\omega }_1}$\frac{\partial\sigma}{\partial\omega_{1}} 表示债券和股票的权重的微小改变会带来总投资组合的多少风险，被称为边际风险（Marginal Risk）。如果令 $p_0=p_1$p_{0}=p_{1} ，则 $\frac{{\omega }_0}{{\omega }_1}=\frac{{\sigma }_1}{{\sigma }_0}$\frac{\omega_{0}}{\omega_{1}}=\frac{\sigma_{1}}{\sigma_{0}} ，即当风险平价时，权重和波动率成反比关系（嗯有点Portfolio Replicate那味了）。

带杠杆与不带杠杆

假定债券和股票的波动率是5%和15%，不难算出对应的持仓占比是75%和25%，即 ${\omega }_0=0.75$\omega_{0}=0.75 ， ${\omega }_1=0.25$\omega_{1}=0.25 ，也即“26/75风险平价组合”，如下图所示。

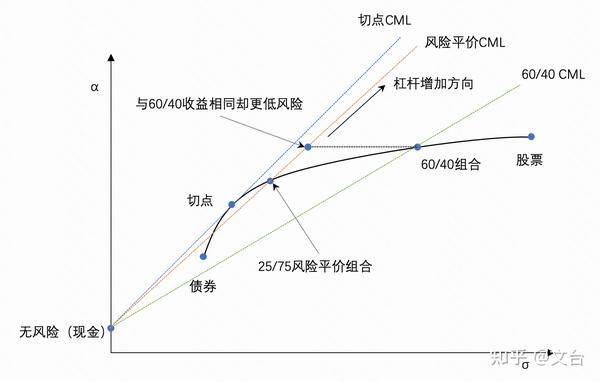
如图所示，25/75比60/40的收益降低了但波动率也大幅下降，对应的夏普比率提高。

因此风险平价组合因为持有的债券过多，风险更低，预期收益也更低，主要是收益率往往难以达到要求。

但是如果考虑进杠杆，情况会好很多，即图中红色虚线所示，我们借贷现金，买入25/75，延杠杆增加的方向，可以达到一个点，在这里与60/40有相同的收益，但风险却大幅降低了。

同时这也揭示了一种常规操作，即当夏普比率有效提高以后，通过杠杆适度地提高预期风险，往往可以获得更令人满意的收益。

中国市场的情形

中国市场的特点是波动率补偿过低，或夏普率过低，市场并没有为波动率提供足够多的补偿，投资价值不高。

如果我们继续从整体时间维度看，2018-2021年的期间内，沪深300指数累计收益22.6%，年化收益5.36%，年化波动率19.9%；中证500指数累计收益率17.7%，年化收益4.28%，年化波动率21.6%；中证1000指数累计收益率14.2%，年化收益3.46%，年化波动率23.5%，投资股指简直可以用惨不忍睹形容。

例如2007-2015，上证从2675涨到3529，涨幅32.25%，但年化的标准差居然高达30%，与此相对债券的中债财富指数从115.8上升到166.2，总收益44%，年化标准差只有2.88%，债券的收益居然更高，而波动率远远低于股票，从这个角度讲，风险平价超配低波动资产的思路在中国的表现会比较好。

风险平价的特点是风险分散，低波动资产被超配，而高波动资产被低配，因此当牛市来临，往往表现不佳。

实践

RPP的构建过程相当简单

第一步：根据各资产的收益率估计协方差矩阵 $\mathrm{\Sigma }$\Sigma

第二步：计算各资产的边际风险Marginal Risk Contribution（MRC），其中资产j 相对投资组合的边际风险等于经过协方差变换后的向量除以组合波动率 $\sigma$\sigma

$MR{C}_j=\frac{\mathrm{\partial }\sigma }{\mathrm{\partial }{\omega }_j}=\frac{(\mathrm{\Sigma }\ast \omega {)}_j}{\sigma }$MRC_{j}=\frac{\partial\sigma}{\partial\omega_{j}}=\frac{(\Sigma*\omega)_{j}}{\sigma}

${\omega }_j$\omega_{j} 表示资产j在投资组合中的权重， $\omega$\omega 表示投资组合的权重行向量， $\sigma =\sqrt{w\mathrm{\Sigma }{w}^{{}^{\prime }}}$\sigma =\sqrt{w\Sigma w^{'}} 表示组合波动率。

第三步：计算各资产对组合的风险贡献 Risk Contribution

$R{C}_j={\omega }_j\ast MR{C}_j=\frac{{\omega }_j\ast (\mathrm{\Sigma }\omega {)}_j}{\sigma }$RC_{j}=\omega_{j}*MRC_{j}=\frac{\omega_{j}*(\Sigma \omega)_{j}}{\sigma}

回测结果：

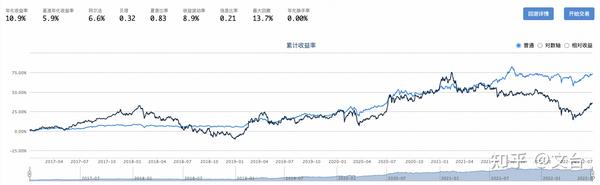
标的：包括了债券，黄金，大宗商品，沪深300ETF，纳斯达克ETF，股票，行业基金等

回测区间：2017-01-01～2022-07-01

回测四年来的数据，对标沪深300，组合的整体波动率显著低于沪深300，在2022年初的大跌时收到的影响也较小，当然年化收益只有10%左右，倒是夏普率可以轻松达到0.8，还是比较惊讶的，考虑到这里的标的选择比较随意，并未上模型，未来做到1以上应该不成问题。