构造微分流形这个概念的动机是什么?
创建时间:2020-07-09 06:42:38
最后编辑:2020-07-09 07:00:40
当我们在说“空间”的时候, 它真的“空”而能“间”物吗? 或者说, 空间和物体有怎样的区别? 一个独特的观点是, 二者是一致的. 当我们在观察桌上的一个杯子时, 我们很自然的认为杯子“处在”这样一个空间之中, 而没有思考过, 实际上, 杯子自身也可以看作一个“空间”, 只是因为它的某些属性较低(比如维度), 使得我们不容易看出它的本质 —— 比如, 对于杯子上面的某个细菌而言, 这个杯子(的表面)完完全全可以看作一个能限制细菌运动的“空间”. 所以我们在说“空间”的时候, 到底是在说什么? 有什么更一般的概念蕴藏其中? 我们能否用统一的语言去描述空间和物?
下面, 我们拿地球做一个例子. 一个有趣的现象是, 即使在现今的教育体制下, 如果没有刻意接受过这方面的知识, 那么一个人很自然地会认为大地是平坦的: 这块儿平坦的曲面上, 有房子、山脉、电线杆和人. 然而现在我们知道, 大地其实更像球面, 称作地球.
为什么看起来像一个平面? 因为它确实很大. 不过, 经过数千年的文明变革, 人们发现了如下证据:
- 古希腊人知道, 如果站在海边的高岩上, 就会看到一条确定的地平线, 它并不太远但是它外边的船只都看不见了. 平坦的大地会很难解释这个现象.
- 向着某一个方向一直走, 若走得足够远, 就会回到出发点地方. 这一点, 早在 15 世纪由 Columbus 和 Magellan 部分完成, 也就是著名的环球航行.
- 如果沿着一条三角形路径旅行, 而这个三角形足够大, 就会察觉出来, 这个三角形的内角和竟然大于 180^\circ. 假设你在行走的过程中, 路径持续笔直, 处处无法察觉大地的弯曲, 那简直就像一直走在一张平面上, 但每到达三角形的顶点就测量角度, 比如分别在北京、上海和广州测量, 会发现内角和并不是 180 度, 这和平面几何是矛盾的. 这仿佛是很有趣的“超自然现象”.
- 在距离“大地”足够远的地方观察“大地”, 会发现它置身于一个更庞大的黑色空间中, 此时大地作为一颗球体而出现. 这一点, 于 20 世纪五十年代多地发射的卫星相继完成. 首次“全身照”则于 1972 年由 NASA 完成.
你会发现, 在之后我们对流形的描述中, 会与上述现象较为相似.

同样是千年来的统治, Euclid 的几何体系一直被认为是描述宇宙的最好的几何学. 这是很自然的. 然而这是不靠谱的, 和相信 2 维 Euclid 体系是描述大地表面最好的模型一样不靠谱. 用 Lorentz 几何学描述的时空模型现在被认为更好地描述了宇宙. 当然, 即使没有狭义相对论, 天文观测也并没有给我们任何特殊的理由, 认为 Euclid 的几何学“最好”. 我们甚至能大胆地类比, 有可能我们的 3 维空间是很大的 4 维球体的表面. 这会导致什么有趣的现象? 类似在地球上走了很长的距离, 就发现“大地平面”的弯曲性质一样, 没准儿我们坐一趟火箭, 飞上足够远的距离且不改变航向, 最终会惊喜地回到原地. 令人惋惜的是, 暂时还没有发现这方面的证据.
1. 微分流形
用数学来描述空间是轻松的, 但我们有必要将上述的概念做一些规范. 现在让我们处在一个 3 维空间中, 只要给出某一坐标系中的三元组 (x,y,z) 就能描述一个点的位置了. 构造一颗 3 维球体的 2 维球面, 即
\{(x,y,z)\in\mathbb R^3|x^2+y^2+z^2=r^2\}.\\
我们说它是 3 维的球体, 因为上面的点都处在 \mathbb R^3 中, 但其实它的自由度只有两个, 因此我们又认为它是 2 维曲面. 这就是所谓外蕴和内蕴的区别. 从外部的环绕空间来看, 地球是空间的一部分, “维数”是 3; 而从内蕴的点与点间关系来看, 大地在局部角度上类似一张 2 维的平面, “维数”是 2. 不同的角度指向了类似的事实, 即至少这个大地不是平坦的.
为什么要做这样的一个区分? 这实际上对应了之后提及的流形定义的不同角度. 内蕴的角度很重要, 因为有时候我们的条件会限制研究, 比如在喷气推进还没有广泛研究之前, 我们暂时看不到“外空间”, 只能从内蕴的角度判断这个大地是平还是曲;亦或是 Klein 瓶,其内禀角度是完全有意义的曲面,但很难在 3 维空间中自然想象,当然,其实放到 4 维就自然许多了.实际上, 我们也不一定必须从外蕴角度去研究一个流形, 特别是当外蕴难以想象时.
比如说, 我现在说我们处在一个 3 维球面之中, 因为普通的平直空间实在是不能描述我们的宇宙了, 假如已经有人发现飞船远离之后又会回归了. 身为科学家的你该怎么研究? 我们可以尝试着, 用 4 个坐标去描述空间, 即 (x,y,z,w), 并加上条件
x^2+y^2+z^2+w^2=r^2.\\
这样我们就把 3 维空间描述为了一个 4 维球体的表面. 这实在是难以想象, 我们的宇宙会有可能生活在一个更大的未曾观测到的 4 维空间中. 但如果采取内蕴的方式定义, 那么 3 维球面 S^3 将不再需要参照任何包含它的空间中.
让我们又回到 2 维球面上. 想象一颗星球, 它可以是《星际穿越》里的水球, 没错, 类似这样一种被平静的水面覆盖的行星. 如果在北极丢了一块大石头进去, 那么水波就会“扩散”, 不断传播, 类似一个半径越来越大的圆. 这个圆任意时刻都是星球的纬圈, 海浪可以是像电影里那么大. 某个恰当的时候, 圈到达了赤道, 之后它竟然会开始“收缩”, 表面上的人觉得很突然. 最终水波到达南极.

类比到 3 维空间中呢? 注意我们现在在一个 3 维球面上, 如果某一点发出了光波, 波是一个不断扩张的(2 维)球面. 让我们始终处在球面的边缘上观察这颗球, 它扩展得很大很大, 一直到它伸展成一个平面了(而它的另一面处在我们看不见的无穷远处). 现在它开始里外翻转, 从一个平面又逐渐收缩, 但收缩到另一个点上去. 这个“内外球皮翻转”的过程并不求助于 4 维空间, 但我们已经观察到, 这样的现象不符合熟悉的 Euclid 空间了. 我们注意到了空间的弯曲. 这种方法的威力在于, 我们可以真正对一个 3 维球面做了一个数学的 3 维描述, 而不是 4 维的.
(*代码*)
Export["sphere.gif",
Table[Graphics3D[{Sphere[{1/a - Sign[a]/(10.125), 0, 0},
Abs[1/a] - 1/(10.125)]},
PlotRange -> {{-1, 1}, {-1, 1}, {-1, 1}}], {a, -10.125, 10.125,
0.25}]]2 维和 3 维球面都是流形的基本例子, 在高阶的数学课程中, 我们还会学到环面、射影平面等. 形象地说, 一个 d 维流形, 简称 d 流形 M, 就是这样的几何对象:
- 流形局部同胚于一个 Euclid 空间. 也就是说, 其间的每一个点的某个邻域, 我们都感到像是 d 维 Euclid 空间(的一部分)包围了这个点. 这我们是知道的, 因为地球表面、环面、射影平面很小的一部分都非常接近于平面(的一部分), 所以它们都是 2 流形, 或者说叫 2 维曲面(但曲面并不一定必须是某个东西的“表面”).
- 我们常常研究所谓的微分流形. 对于一个具有可微结构(性质)的流形, 可以是一个自然空间, 一个物体, 一杯茶, 我们在其中能做一些微积分.
2. 图
说回地球表面的问题,其内禀观念就是用所谓的图册“2 维”地观察曲面.“图”的字眼其实是从地图学和大地测绘学中借用的,其含义自明.处理流形的一个更一般的途径就是用描述“局部”确切含义的图册.
一本世界地图集, 一本真正生活意义中的图册书, 是由许多平面的地图页装订而成. 我们假设一张是中国地图, 一张是俄罗斯地图. 这两张在绘制上显然有重叠的地方, 我们有必要说明. 因为这两个国家是紧挨的, 中间夹着蒙古, 它在两页地图上都可以找到. 我们要说清楚蒙古在中国地图的北部, 而在俄罗斯地图的南部. 抽象就是, 这一页的某点, 对应于另一页的哪点. 虽然一个图册画的是 3 维宇宙中的一个对象, 但是地球表面的球面几何却只需从平面的图页上读出. 这是自古以来的智慧. 这件事做起来虽然不太方便, 但其实是可能的, 即我们甚至可以描述地球的旋转, 比如它只需要让第 27 页的澳大利亚移动到 34 页的某个位置, 此时图册的每一页的图都跟着变化了.
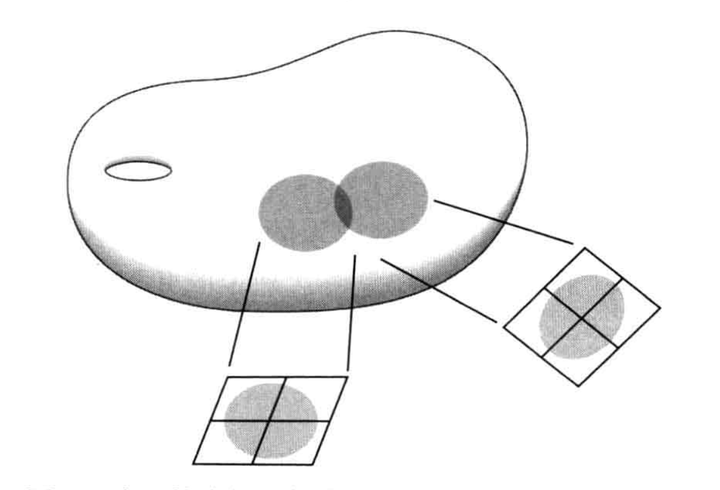
一个 2 维流形可以这样用 2 维图册来定义. 一个 2 维球面可以这样用数学描述: 这本图册只有两页, 每一页都呈圆形. 一页是北半球, 但是稍大一些, 越过赤道以便于南半球部分重叠; 一页是南半球, 但也包含北半球邻近赤道的一部分. 这两页地图都是平坦的平面, 之上的岛屿可能会有些扭曲, 但我们也能说明出其扭曲程度.

图册的概念很容易推广到 3 维情况. 只不过, 现在每一页都变成了 3 维空间(的一部分). 我们说这样的页叫作图, 也叫坐标卡. 我们之前提到流形局部同胚于(对应维度)欧氏空间的一部分, 这就说明存在一个同胚映射 \phi 把流形上的点 x 一一对应地投到了欧氏空间中的 \phi(x), 同胚便让这两个点等同起来了, 就可以认为 \phi 是坐标区图. 这样我们就可以利用 \phi(x) 的坐标描述 x 了.
那么, 上面的例子中, 就可以认为一张标准的中国地图把地球表面上的中国部分的一个点与一个平坦的 2 维纸面上的点等同起来了, 成了一张标有经纬度的网格——经纬度自然是地图上的坐标系, 它可以对应转换到地球上的坐标系.此即是说,一个图把流形一部分与其同维的欧氏空间之一部分等同起来.
一个 3 维图册就是若干 3 维图的集合, 当然也要指明, 一个图的某部分对应于另一图的哪些部分. 3 维球面有一个图册, 这个图册类似地包含了两个立体的 3 维球体. 在一个球体靠近边缘(球面)的部分的点与另一球体靠近其边缘部分的点之间有一个对应. 我们所需的几何学齐备了: 当你来到某个球体的边缘附近时, 就会发现已经走到了重叠的区域, 而平滑过渡地, 同时走到了另一个球体里去. 如果再往前走, 就一个球体而言, 你已经离开了它的地图, 但是第二个球体将你接送了过去.
实际上, 图册本身就属于流形. 我们将流形视作图册, 连带着图每个部分互相对应的规则. 在脱离特殊的情景外, 我们用图和图册去定义流形是最方便的一般途径.
Nash 定理指出, 可以认为所有的流形都是外蕴角度产生的, 即把一个 d 流形视作生活在更高维空间中的 d 维超表面. 但是要注意, 想总是找出一个简单数学来定义这个超曲面不是个容易的事情. 但我们知道我们在描述流形, 是因为内蕴上, 每一点的小邻域看起来都像 Euclid 空间. 也就是说, 无论哪种构造方式, 只有对象“局部同胚于 d 维 Euclid 空间”, 就可以认为构造了一个 d 流形.
微分流形的一个重要性质是可以对定义其上的函数做微积分. 积分要引入微分形式的概念, 下面我们只考虑微分. 设 M 是一个流形, 和一个函数(也叫标量场) f:M\to\mathbf R, 要判断 f 是否在 x\in M 可微, 首先要取 M 的一个包含 x 的图, 并认为 f 是定义在该图上的函数. 因为图是 \mathbf R^d 的一部分, 其中我们本就可以做微分, 所以可微性是 f 具备的. 要使其可微性定义在流形上, 需要指出 f 属于两个重叠的邻域(坐标域)和图(坐标系), 并对两个同时具备的图可微. 交集处在两个图 \phi,\psi 下映射为 \mathbf R^d 的两个(通常)不同的开集, 这两个开集便也就等同起来了, 它们给出了不同的坐标.这个关系就是转移(迁移)函数, 或者叫坐标变换, 比如可以是从 \phi 下的坐标 x 变换到 \psi 中的 \psi(\phi^{-1}(x)). 自然, 迁移函数就是两个图之间的同胚.如果坐标变换是可微的, 那么同时可微性也就有保证了.
上述思想容易从实数值函数推广到 f:M\to\mathbf R^n 上去, 甚至是 f:M\to M' 的映射. 然而, 判断流形上的函数是否可微, 其实比求导要容易. 一个函数 f:\mathbf R^n\to \mathbf R^m 在 x 的导数是线性映射, 定义在流形上的函数也采取类似的方法. 不过注意的是, 该线性映射的定义域不是流形本身, 而是在 x 处的切空间. 随后, 我们能一路构造微分形式及其积分, 不过这些都是后话了.
更多回答
根据维基百科的说法:
Hermann Weyl gave an intrinsic definition for differentiable manifolds in his lecture course on Riemann surfaces in 1911–1912, opening the road to the general concept of a topological spacethat followed shortly. During the 1930s Hassler Whitney and others clarified the foundational aspects of the subject, and thus intuitions dating back to the latter half of the 19th century became precise, and developed through differential geometry and Lie group theory.
你现在看到的“局部欧氏第二可数的Hausdorff空间”这种公理化定义是20世纪才出现的。但是具体的流形的例子在之前就已经出现了。比如19世纪黎曼就提出了黎曼曲面的概念。Abel和Jabobi对椭圆积分的研究导致他们开始考虑某些特殊的复流形。19世纪分析力学的发展导致力学家们逐渐产生 辛流形 的概念。还有李群理论的发展。等等等等。具体可以看看这个维基页面:
The term "manifold" comes from German Mannigfaltigkeit, by Riemann.
In English, "manifold" refers to spaces with a differentiable or topological structure, while "variety" refers to spaces with an algebraic structure, as in algebraic varieties.
In Romance languages, manifold is translated as "variety" – such spaces with a differentiable structure are literally translated as "analytic varieties", while spaces with an algebraic structure are called "algebraic varieties". Thus for example, the French word "variété topologique" means topological manifold. In the same vein, the Japanese word "多様体" (tayōtai) also encompasses both manifold and variety. ("多様" (tayō) means various.)
我们现在课本上的讲授顺序,是先讲抽象定义,再讲具体例子。比如课本上先给你定义什么是流形,什么是群,然后告诉你 一个有相容的群结构的光滑流形叫李群。然而历史上的发展顺序往往是反过来的。具体的矩阵群李群的例子出现在流形的公理化定义之前;19世纪没有代数簇的严格定义,但是已经有意大利代数几何学家研究代数曲面了。是一大堆的例子驱使出数学家抽象出概念的共性,从而提出总括性的一般定义。而不是数学家先高屋建瓴提出一个抽象定义,然后再凭空造出一大堆例子。正如数学发展的初期,先出现的是平面几何,是初等数论,而不是ZFC集合论。
我不敢说提出流形这个概念的历史动机是什么,就说说自己的理解吧。
比方说,古代的时候,很多人并不知道地球的形状是什么样的。从人们对局部空间的几何感知出发,人们无法推测出地球的整体几何特征,到底是球形,梨形或是面包圈形的。但另一方面,人们很早就学会了画地图,知道可以用平直的二维空间来表示局部的地形特征。
现在我们知道,地球表面不是平直的,严格说来也不是规则的球面,甚至我们身处的三维空间,也不见得是规则,均匀,平直的,但这并不妨碍人们运用朴素的理性建立起平直均匀的二维,三维欧氏空间,用以描写自己所处的局部环境。
流形,就可以看做这一经验的推广和抽象提炼。流形其实就是说,一个n维的几何体,我们不知道它整体的几何性质如何(比如地球),但我们对它的每一个局部,都能用n维欧氏空间来描写(比如n=2时,用地图描写地表局部)。
用术语来说,这个“局部”,就是拓扑空间中的开集,用n维欧氏空间描写,就是说能够建立开集到n维欧氏空间的“微分同胚”。粗略地说,微分同胚就是一种保持拓扑结构(可以理解成空间中点与点的邻接关系)与微分结构的一一映射。你可以认为,流形的每个局部,从拓扑和微分结构的角度看,都“等价”于n维欧氏空间的一个局部,进而,也就能够赋予其一个局部的坐标系。
这就是流形概念的第一层意思,也是最直观,最精髓的一点:流形的局部等价于欧氏空间,我们可以在其上建立局部坐标系,建立方向(切丛),直线(测地线)这些概念(地球表面并不平坦,但并不影响我们建立了直线和方位的概念)。
在流形概念建立之前,我们一般来说是把n维几何体嵌入到n+1维欧氏空间中去研究的。也就是说,几何体上的每一个点,都被赋予了一个“绝对坐标”。
有了流形的概念之后,我们就不一定要将几何体嵌入到高维欧氏空间了。我们在每个局部,都可以赋予一个相对坐标,这就是流形的研究方式。
仔细说起来,n维几何体还不一定能嵌入到n+1维欧氏空间中。微分拓扑学的结论表明,n维几何体可能要嵌入到最多2n+1维欧氏空间中。比如,挠率不为零的曲线就只能嵌入到3维欧氏空间中。经典曲面论研究的往往是嵌入到3维空间中的可以可视化的曲面,但是2维曲面Klein瓶就至少要嵌入到4维欧氏空间中。这意味着,同样是n维几何体,由于嵌入的欧氏空间的维度不同,其表示形式就不相同。反过来,用流形的观点,倒突出了几何体内禀的维度。
当然,我们知道,作为近似球面的地球表面,是无法在毫无变形,毫无失真的情况下,用一张张平面地图拼接起来表示的。此外,绘制地图,也有着不同的比例尺和各种各样的投影方法,会造成不同种类,程度的扭曲,失真。但只要它们满足一定条件,我们就认定它们绘制的是同一地图,或者它们能够以某种方式拼接起来,表示某个几何整体。
在数学上,我们说流形上各个局部到n维欧氏空间的微分同胚之间,要满足一个特定的相容性条件。同一个点,可以属于不同的开集,赋予不同的坐标表示;同一个开集,也可以赋予不同的坐标表示,只要这些表示是“相容”的。这就好比,地图有各种画法,只要满足一定的相容性条件,我们就认定这些地图是对同一几何体进行描绘,且这些局部的地图总能以某种方式拼成整体的样子。
这就是流形概念的第二层意思:流形的局部微分同胚于n维欧氏空间,这些微分同胚之间彼此是相容的。
一般来说,运用第一层意思,我们已经能够做很多事情了。只要有了局部同胚,局部坐标表示,我们大致上就可以开发出粗糙版本的切丛,联络,测地线,曲率等概念了。但是,为了严谨起见,我们需要论证,我们提出的这些概念,在更换另一个局部坐标之后,不会发生变化,也就是说,我们的概念是几何体内禀的,而不是和坐标系的选取相关的。这时,我们就往往需要援引相容性条件,也就是刚刚说到的流形概念的第二层意思了。
最后,由于局部坐标系的存在,我们很容易在局部定义一个张量场,比如黎曼度量,但怎么将局部的张量场延拓,或者拼接成整体性的张量场呢?这里,常常要用到微分拓扑的基础知识,“单位分解定理”。由于“单位分解定理”需要拓扑空间满足第二可数公理才成立,所以我们要求流形的拓扑空间满足第二可数公理,这是流形概念的第三层意思。
综上,流形最核心的,最直观的要点是,它在每个局部可以同胚于欧氏空间,可以建立局部坐标。但为了概念打磨的目的,还需引入相容性条件和第二可数公理。第一条说的,是流形的局部性质,是流形概念的直觉所在,后两条说的,是局部与局部的关系,局部与整体的关系。照我理解,主要是要排除掉那些“病态”的情况(比如几何量或公式在不同的局部标架下表示不一致,或者局部场无法拼接延拓为整体量,等等)。
从某种角度看,局部的欧氏特性和整体的非欧特性,被统一在流形这个结构中,就好像地球,我们从局部认识它那就是欧氏几何,从整体认识它那就是非欧的黎曼几何,也或许流形的提出反映了人们从欧氏几何到反直觉的非欧几何再到更加一般的几何学这样一种认知的探索吧。
个人建议是,如果没有数学系的看懂定理证明的需求,其实可以满足于知道流形就是每个局部等价于欧氏空间的几何体就足够了。




