5.12: Evanescent Waves 5.12: 倏逝波
Consider the situation shown in Figure :
考虑图 所示的情况:
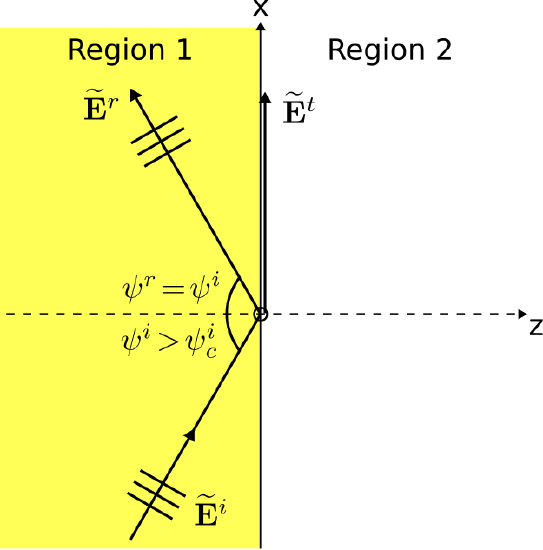 Figure : A uniform plane wave obliquely incident on the planar boundary between two semi-infinite material regions. Here and . ( CC BY-SA 4.0; C. Wang)
Figure : A uniform plane wave obliquely incident on the planar boundary between two semi-infinite material regions. Here and . ( CC BY-SA 4.0; C. Wang)
图 :倾斜入射到两个半无限材料区域之间的平面边界上的均匀平面波。这里 和 。 (CC BY-SA 4.0;C. Wang)
A uniform plane wave obliquely incident on the planar boundary between two semi-infinite material regions, and total internal reflection occurs because the angle of incidence is greater than the critical angle
均匀平面波倾斜入射到两个半无限材料区域之间的平面边界上,由于入射角 大于临界角,发生全内反射
Therefore, the reflection coefficient is complex-valued with magnitude equal to 1 and phase that depends on polarization and the constitutive parameters of the media.
因此,反射系数是复值,其幅度等于 1,相位取决于介质的偏振和本构参数。
The total reflection of the incident wave seems to contradict the boundary conditions that require the tangential components of the electric and magnetic fields to be continuous across the boundary. How can these components of the fields be continuous across the boundary if no power is transmitted across the boundary? There must be a field on the opposite side of the boundary, but – somehow – it must have zero power. To make sense of this, let us attempt to find a solution for the transmitted field.
入射波的全反射似乎与要求电场和磁场的切向分量在边界上连续的边界条件相矛盾。如果没有能量跨越边界传输,这些场的分量如何能够跨越边界连续?边界的另一侧一定有一个场,但不知何故,它的功率必须为零。为了理解这一点,让我们尝试找到传输场的解决方案。
We begin by postulating a complex-valued angle of transmission . Although the concept of a complex-valued angle may seem counterintuitive, there is mathematical support for this concept. For example, consider the well-known trigonometric identities:
我们首先假设一个复数值的传输角度 。尽管复值角度的概念可能看起来违反直觉,但这个概念有数学支持。例如,考虑众所周知的三角恒等式:
These identities allow us to compute values for sine and cosine even when is complex-valued. One may conclude that the sine and cosine of a complex-valued angle exist, although the results may also be complex-valued.
这些恒等式使我们能够计算正弦和余弦的值,即使 是复数值。人们可能会得出这样的结论:复值角度的正弦和余弦存在,尽管结果也可能是复值。
Based on the evidence established so far, we presume that behaves as follows:
根据迄今为止建立的证据,我们推测 的行为如下:
In other words, is identical to for , but when total internal reflection occurs, we presume the real part of remains fixed (parallel to the boundary) and that an imaginary component emerges to satisfy the boundary conditions.
换句话说, 与 的 相同,但是当发生全内反射时,我们假设 的实部保持固定(平行于边界),并且虚部 出现以满足边界条件。
For clarity, let us assign the variable to represent the real part of in Equations -. Then we may refer to all three cases using a single expression as follows:
为了清楚起见,让我们分配变量 来表示方程 的实部> - 。然后我们可以使用单个表达式来引用所有三种情况,如下所示:
Now we use a well-known trigonometric identity as follows:
现在我们使用众所周知的三角恒等式,如下所示:
Using Equation , we find:
使用方程 ,我们发现:
In other words, the cosine of is simply the hyperbolic cosine (“”) of . Interestingly, of a real-valued argument is real-valued, so is real-valued.
换句话说, 的余弦只是 ”) b4> 。有趣的是,实值参数的 是实值,因此 是实值。
Using Equation , we find:
使用方程 ,我们发现:
In other words, the sine of is times hyperbolic sine (“”) of . Now note that of a real-valued argument is real-valued, so is imaginary-valued.
换句话说, 的正弦是 倍双曲正弦(“ ”) 。现在请注意,实值参数的 是实值,因此 是虚值。
Using these results, we find Equation may be written as follows:
使用这些结果,我们发现方程 可以写成如下:
Using precisely the same approach, we find:
使用完全相同的方法,我们发现:
Before proceeding, let’s make sure Equations and exhibit the expected behavior before the onset of total internal reflection. For , and . In this case, , , and Equations and yield
在继续之前,让我们确保方程 和 在全内反射开始之前表现出预期的行为。对于 、 和 。在这种情况下, 、 和方程 和 产量
as expected. 正如预期的那样。
When total internal reflection is in effect, , so . In this case, Equations and yield
当全内反射生效时, ,因此 。在这种情况下,方程 和 得出
Let us now consider what this means for the field in Region 2. According to the formalism adopted in previous sections, the propagation of wave components in this region is described by the factor where
现在让我们考虑这对于区域 2 中的场意味着什么。根据前面章节中采用的形式,该区域中波分量的传播由因子 描述在哪里
and
so
Therefore, the wave in Region 2 propagates according to
因此,区域 2 中的波按照以下方式传播:
Note that the constants and are both real-valued and positive. Therefore, Equation describes a wave which propagates in the direction, but which is not uniform. Specifically, the magnitude of the transmitted field decreases exponentially with increasing ; i.e., maximum at the boundary, asymptotically approaching zero with increasing distance from the boundary. This wave is unlike the incident or reflected waves (both uniform plane waves), and is unlike the transmitted wave in the case (also a uniform plane wave). The transmitted wave that we have derived in the case gives the impression of being somehow attached to the boundary, and so may be described as a surface wave. However, in this case we have a particular kind of surface wave, known as an evanescent wave. Summarizing:
请注意,常数 和 都是实值且为正值。因此,方程 描述了沿 方向传播的波,但该波不均匀。具体来说,发射场的大小随着 的增加呈指数下降;即边界处的最大值,随着与边界的距离的增加而渐近地接近零。该波不同于入射波或反射波(均为均匀平面波),也不同于 情况中的透射波(也是均匀平面波)。我们在 情况下导出的透射波给人以某种方式附着在边界上的印象,因此可以被描述为表面波。然而,在这种情况下,我们有一种特殊的表面波,称为倏逝波。总结:
When total internal reflection occurs, the transmitted field is an evanescent wave; i.e., a surface wave which conveys no power and whose magnitude decays exponentially with increasing distance into Region 2.
当发生全内反射时,透射场是倏逝波;即,表面波不传递功率,其幅度随着进入区域 2 的距离的增加呈指数衰减。
At this point, we could enforce the “phase matching” condition at the boundary, which would lead us to a new version of Snell’s law that would allow us to solve for in terms of and the constitutive properties of the media comprising Regions 1 and 2. We could subsequently determine values for the phase propagation and attenuation constants for the evanescent wave. It suffices to say that the magnitude of the evanescent field becomes negligible beyond a few wavelengths of the boundary.
此时,我们可以在边界处强制执行“相位匹配”条件,这将导致我们得到斯涅耳定律的新版本,使我们能够求解 项以及包含区域 1 和 2 的介质的本构属性。我们随后可以确定倏逝波的相位传播和衰减常数的值。可以说,在边界的几个波长之外,倏逝场的大小变得可以忽略不计。
Finally, we return to the strangest characteristic of this field: It acts like a wave, but conveys no power. This field exists solely to enforce the electromagnetic boundary conditions at the boundary, and does not exist independently of the incident and reflected field. The following thought experiment may provide some additional insight.
最后,我们回到这个场最奇怪的特征:它的行为像波浪,但不传递任何力量。该场的存在只是为了加强边界处的电磁边界条件,并且不独立于入射场和反射场而存在。下面的思想实验可能会提供一些额外的见解。
In this experiment, a laser illuminates a planar boundary between two material regions, with conditions such that total internal reflection occurs. Thus, all incident power is reflected, and an evanescent wave exists on the opposite side of the boundary. Next, the laser is turned off. All the light incident on the boundary reflects from the boundary and continues to propagate to infinity, even after light is no longer incident on the boundary. In contrast, the evanescent wave vanishes at the moment laser light ceases to illuminate the boundary. In other words, the evanescent field does not continue to propagate along the boundary to infinity. The reason for this is simply that there is no power – hence, no energy – in the evanescent wave.
在此实验中,激光照射两个材料区域之间的平面边界,条件是发生全内反射。因此,所有入射功率都被反射,并且在边界的另一侧存在倏逝波。接下来,关闭激光。所有入射到边界上的光都会从边界反射并继续传播到无穷远,即使在光不再入射到边界上之后也是如此。相反,倏逝波在激光停止照射边界时消失。换句话说,渐逝场不会继续沿着边界传播到无穷远。原因很简单,倏逝波中没有能量,因此也没有能量。


