扩散模型与能量模型，Score-Matching和SDE，ODE的关系

这篇文章主要是想简单总结下自己最近了解的扩散模型与一系列研究方向的关系。之前写过一篇扩散模型与这些个名词间的关系，但总结得不够好。这一篇将以新的行文思路梳理自身所得。

这篇笔记主要参考以下论文和参考资料：

1. SCORE-BASED GENERATIVE MODELING THROUGH STOCHASTIC DIFFERENTIAL EQUATIONS-SongYang
2. How to Train Your Energy-Based Models-SongYang
3. Tutorial on Denoising Diffusion-based Generative Modeling: Foundations and Applications

1. 主流生成模型的缺陷

深度生成模型一直是机器学习研究领域关注的重点方向。其重点在于如何建模和拟合复杂的数据分布。为了实现这个目标业界提出了各种各样的深度生成模型，比如变分自编码器（VAE），正则化流（Normalization Flow）, 生成对抗网络（GAN），自回归模型（Autoregressive Model）等。这些模型各有各的优点和缺点。比如VAE最大的问题在于如何建模目标后验分布q(z|x)和先验分布p(z)。主流的做法是将这两个都建模为高斯分布，这样既方便采样也方便计算先验和后验分布间的距离（KL散度）。但很明显VAE最大的问题在于如何建模这两个分布，如果设计得太复杂，既不方便采样，也难以计算KL散度。但选取得简单了又难以表征复杂的数据分布。而正则化流虽然使得准确的概率似然函数计算成为了可能，但其最大的限制在于其每一步的计算要求是一个可逆函数，这也限制了正则化流每一步的变换所可以选缺的函数的范围，也影响了整体的拟合能力。GAN和自回归模型的问题也很明显。GAN最大的问题在于训练特别不稳定，难以拟合容易模式坍塌。而自回归模型在图像界面临的最大问题是生成速度太慢解码空间太大，难以生成高分辨率图像。

虽然以上每个问题你可能都可以找到些反例，比如自回归模型可以结合VAE生成高分辨率图像（例如VQGAN），扩散模型可以看作是马尔可夫层级VAE（MHVAE） ，VAE可以使用正则化流建模先后验分布等。但以上这些问题客观存在，且也是研究领域的一些核心痛点。

那么扩散模型相比于它们的优势到底在哪里？笔者认为有多个。首先扩散模型的建模效果好，能够准确地建模数据分布。 其次扩散模型的损失函数构建特别简单，训练特别稳定。在GAN的时代有大量工作围绕如何稳定GAN的训练展开，但在扩散模型的时代这样的工作比较少见。而且如果深入挖掘的话，扩散模型除了可以看作是MHVAE之外，甚至还可以看作是能量模型（EBM），连续正则化流（CNF）的特殊形式！博取众长的结果就是这些模型的优点它也有。例如类似于正则化流的准确似然计算，无需额外训练即可做到反向使用（比如图像超分，上色，填充，文生图），还拥有能量模型的模型架构的选择自由度高，表达形式丰富等优点。

2. 从能量模型到Score-Matching

首先，对于拟合数据分布这件事，最常见的做法就是最大似然估计（MLE）： 即真实数据分布里采样出来的数据要能够在你建模的数据分布里概率最大化。

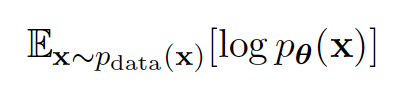
而如果将建模的数据分布写成更加通用的能量模型形式，我们会遇到一个很大的麻烦，即如何计算能量模型的配分函数Z。对于绝大部分的能量函数来说，其归一化函数Z的求和都是一件难以计算的事。为了解决这个问题，传统的似然模型做出了不同程度的妥协。如自回归模型假设了单向依赖的卷积，自回归流要求可逆计算，VAE使用变分下界近似且近似的计算还依赖于先后验形式的强假设等。

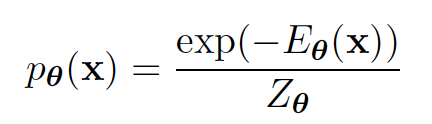
但实际上，能不能不对能量模型的形式做太多约束，直接计算最大似然呢？主流的思路有两种：一种是用MCMC的方法，一种是用Score-matching的方法。

首先简单介绍一下用MCMC做最大似然计算的方法：通过计算对数似然函数的梯度，我们可以用随机梯度下降来优化我们的能量模型。具体来说我们对能量模型的参数求导可得下式，其中左侧可以直接计算，而右式虽然难以计算但可以转换为其他等价形式（具体推导请参考^[1]）

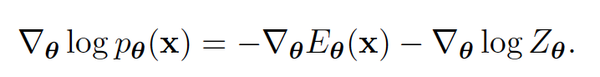
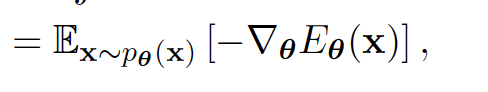
那么对于右式的计算就转换成了在我们建模近似的数据分布 $P_{\theta }$P_{\theta} 里采样出点，来估计期望的问题了。对于在复杂分布里采样最广为应用的方法莫过于MCMC了。具体来说，我们可以通过估计$P_{\theta }$P_{\theta} 对输入x的梯度（称为score）来实现MCMC的游走采样。注意使用score来进行MCMC的一个重要原因就是score的计算不涉及归一化函数Z的计算：

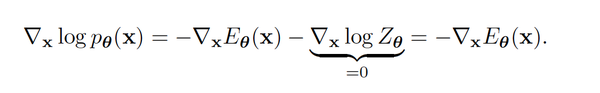
而有了score后，我们可以使用朗之万动力学采样（Langevin-MCMC）在当$ϵ$\epsilon 足够小而迭代步数K又足够大的情况下来近似从 $P_{\theta }$P_{\theta} 里采样。

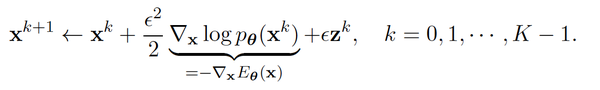
那么总结下用MCMC来计算能量模型的方法，我们对能量模型参数的每一次随机梯度更新，都需要使用MCMC来近似从分布里采样，来估计梯度的计算。这个做法最大的问题就是计算量非常大。

而有了一个准确的能量模型后，我们从数据分布里采样就转换成了根据训练好的能量模型的score, 来进行MCMC采样。那么换个思路，我们能不能直接将能量模型建模成score，即用一个神经网络来拟合score! 这个方法就叫score-matching!

Score-matching的目标是使得真实数据分布对输入x的对数似然的梯度（score）和我们所建模的近似分布的score一致。这背后的原因是如果两个可微函数f(x), g(x)的一阶导数处处相等，则f(x) = g(x) + constant, 而又因为当f(x)和g(x)是对数概率密度方程，他们的积分和为1，所以如果这两个方程的一阶导数处处相等，则f(x) = g(x)。

当然，即使直接建模score我们依然逃不开Pdata的计算，但有大量的工作让我们可以直接计算score-matching，而不需要计算Pdata。同时这些方法还足够快，只涉及到一阶导数的计算。有兴趣的可以查看宋飏博士的sliced score matching 论文^[2]。

3. Score Matching和DDPM的联系

上面我们提到了能量模型和score-matching，但是这和扩散模型有什么关系？

在上一节我们提到我们有了score-function的神经网络近似后，我们可以使用朗之万动力学来采样得到目标分布的样本。但如果只朴素地使用以上定义的score_matching会有以下两个问题^[3]：

1. 大部分我们希望拟合的数据（比如图像）在高维空间里表现为低维流形。而大部分采样的点不落在低维流形上则其概率为零，对零概率的点取对数（score的定义是logP(x))无意义。
2. score function的优化目标是个L2范数的期望，而对于低密度的区域该期望因无法得到足够多的样本来监督训练，其准确度也不高。该问题和以上的低维流形问题一起加剧了采样结果的不理想情况。

而根据宋飏博士的论文^[3]，以上两个问题都会被往数据里添加高斯噪声所解决。

1. 高斯噪声的定义域是整个参数空间，所以对原数据添加高斯噪声解决了低维流形的零概率问题。
2. 添加大量的高斯噪声实质上扩展了分布里的各个众数的范围，使得数据分布里的低概率区得到了更多监督信号。

但是高斯噪声的尺度选择不是个简单的问题，加过大的噪声虽然会覆盖更多的低概率空间，但同时也会剧烈地改变原数据分布，但过小的噪声又会使得低概率空间的监督信号不足。而作者最终采用的方案是添加一系列不同尺度的噪声，并训练一个条件于噪声大小的score matching 网络（noise-conditioned-score-based-model）对他们进行拟合！而这，就自然地对应了以下扩散过程：

当我们有了不同尺度的扰动之后，我们的score-matching目标便变成了对不同程度的噪声的L2范式损失进行加权求和的整体优化。

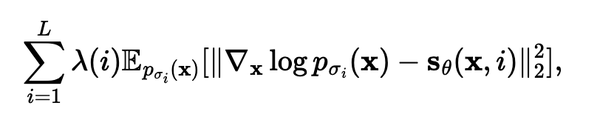
当然，求这个期望要求我们能够直接从 $P_{{\sigma }_i}$P_{\sigma_i} 里直接采样，但那是我们的训练目标我们也并没有该分布的表达形式。但和DDPM的做法一样，我们可以使用祖先采样(ancestral sampling)的方法将边缘分布P(xt) 转化为联合分布P(x0, xt) = P(x0)*P(xt|x0).在将上式里的$P_{{\sigma }_i}$P_{\sigma_i}换成祖先采样后的点后我们可以得到下面这个优化目标

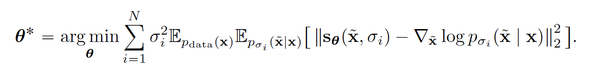
以上我们从score-based-generative-model的角度复盘了score-matching和扩散模型的关系。那么这个Score model 和DDPM又有什么关系？实际上DDPM的训练目标完全等价于我们上面推演的score model的训练目标。

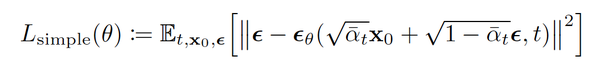
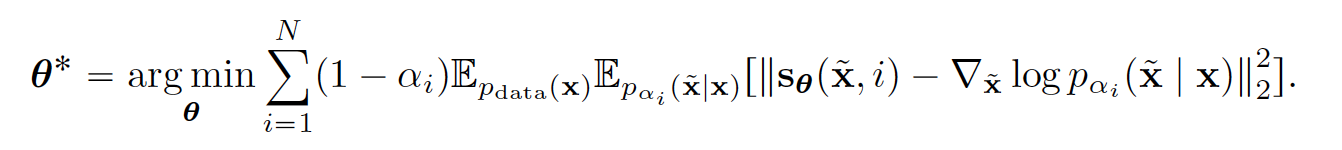
乍一看这两个训练目标并没有明显的实质联系，但实际上他们经过转换后是完全等价的。转换关系如下：

首先我们知道前向扩散的扩散核是高斯核，也知道利用高斯分布的聚合性质后xt关于x0依然是一个高斯分布，其表达形式如下

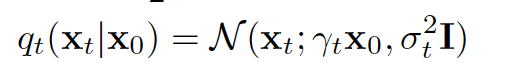
根据上面的高斯分布表达式，我们可以得到以下score function的表达式，其核心在于对score function的求导，实质上使得我们约掉了xt, x0 使得最后的表达式只剩下关于噪声epsilon的项。

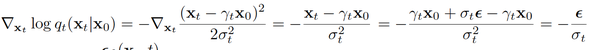
在笔者另外一篇笔记 “中森：大一统视角理解扩散模型Understanding Diffusion Models: A Unified Perspective 阅读笔记 “ 里，笔者也简单记录过这两个形式的等价原因：

4. SDE & ODE

为什么我们要关心Score-based Model。因为它的推演是一个更加自然且符合直觉的过程。而更重要的是，score-matching的提出者宋飏博士将朗之万动力学采样，score matching，随机微分方程SDE和常微分方程ODE联系在了一起。而扩散过程的SDE有确定的ODE对应解代表着我们可以借用业界一直在研究的ODE求解器，快速求解（在几十步内）从而避开了扩散所需几千步的庞大计算量。同时，将扩散由离散向连续统一，使得条件控制生成变得特别自然^[4]。

下面我们来看看扩散过程和SDE的相关联系。我们知道前向过程是一个高斯扩散过程，而关于这个过程如果我们将这个离散的过程连续化，把离散的beta_t 用一个关于时间步的方程${\beta }_t=\beta (t){\mathrm{\Delta }}_t$\beta_t = \beta(t)\Delta_t来表示则前向过程可以表示为下图的2式，而当delta_t足够小时，对2式做一阶泰勒展开可以得到其近似解（具体推导可以看论文^[4]里的附录B, 核心是将beta缩放和连续化表示）。

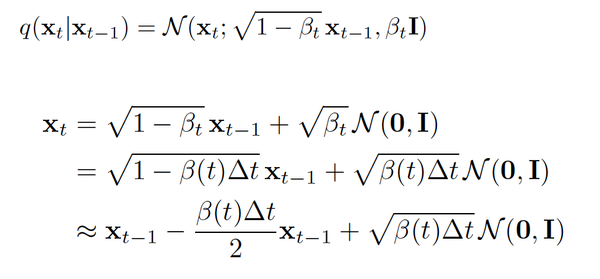
同时，注意这个前向过程的表示实质上就是伊藤扩散的随机微分方程的表现形式

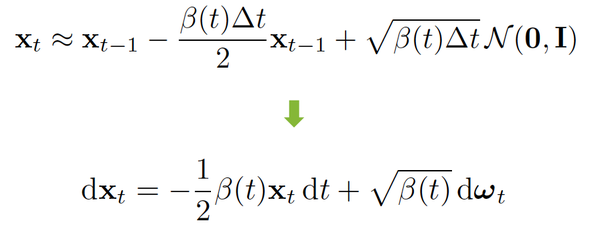
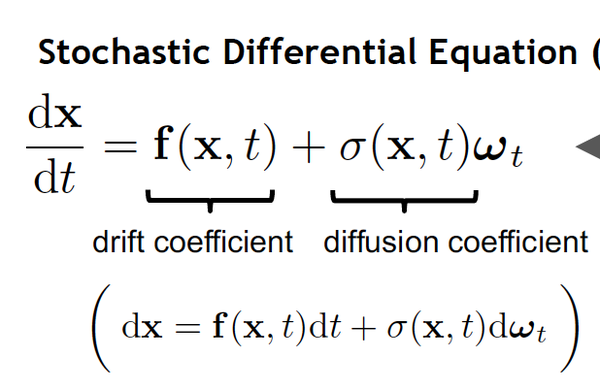
那么既然我们知道了前向过程是一个SDE了，很自然的问题便是后向过程是一个什么形式。巧合的是，一个SDE的逆向过程也是一个SDE，并且在82年的一篇paper里便已被证明。证明的过程非常复杂，有兴趣的读者可以参照这一篇博客^[5], 但现在我们可以直接使用其结论：

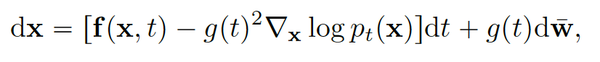
而代入我们上面的扩散方程后可以得到以下SDE的形式，注意熟悉的score function又出现了，这也和上文我们所提及的不同程度的扰动使得score matching更加健壮并且使得在概率空间使用朗之万动力学游走采样成为可能。

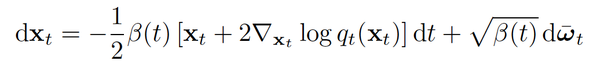
在正向和逆向的扩散过程都可以用SDE表示后，宋飏博士还接着提供了SDE和ODE之间的联系。在论文^[4]的附录D里附上了每个扩散过程都有对应的确定性ODE的形式使得其边缘分布Pt(x)与SDE一致的证明。以下是其一般形式和代入上面的DDPM扩散核系数后的ODE形式（注意其和SDE形式的高度相似，如score function的系数不同，删去了噪音项）

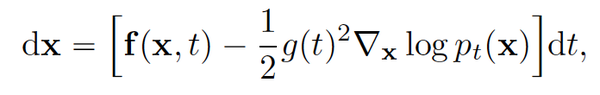
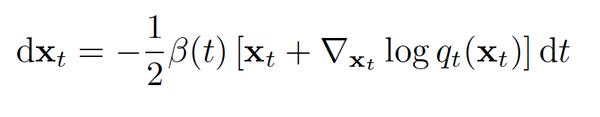
至此我们终于快速地过了一遍扩散模型与SDE/ODE的联系。而将扩散模型转换为这两种形式后，也使得我们利用一系列SDE/ODE求解器成为可能。比如陈天奇2018年的Neural ODE (也就是torchdiffeq库)。

而不止于此，宋飏博士还创造性地提出了以下洞见：我们在随机微分方程的逆向求解过程中，我们不仅可以求解p0(x0)，还可以求解P0(x0|y)即条件概率分布，如果Pt(y|x_t)是已知的。这直接催生了一系列下游条件生成任务的应用例如上色，类别生成，图片补全等。而在文本领域，笔者写过一篇在VAE隐空间直接做条件引导扩散的笔记，也可以看作是宋飏博士这篇论文的洞见的产物。

5. 总结

我们在这一篇文章里梳理了扩散模型和能量方程，朗之万动力学采样，Score-matching, 随机微分方程和常微分方程的联系。这些联系是背后一系列突破得以出现的原因（比如更准确的似然估计和采样，更快速的采样生成和条件生成等）。了解了这些基础联系后，笔者再看一些论文比如文本生成里在VAE潜在空间做扩散ODE，probabilistic ODE是如何在语义空间插值等就觉得水到渠成了。希望这些对读者有些帮助。后面笔者会继续修改和完善这篇笔记，增添一些其他细节。

参考

1. ^How to Train Your Energy-Based Models-SongYang
2. ^Sliced Score Matching: A Scalable Approach to Density and Score Estimation
3. ^^abYang Song and Stefano Ermon. Generative modeling by estimating gradients of the data distribution. In Advances in Neural Information Processing Systems, pp. 11895–11907, 2019.
4. ^^abcSCORE-BASED GENERATIVE MODELING THROUGH STOCHASTIC DIFFERENTIAL EQUATIONS
5. ^reverse SDE explained https://www.vanillabug.com/posts/sde/