1.3 Solving systems of linear equations: matrix inversion and Cramer's rule
1.3 求解线性方程组:矩阵求逆和 Cramer 规则
Two equations in two variables
两个变量中的两个方程
Consider a system of two equations in two variables x1 and x2:
考虑一个由两个变量 x1 和 x2 中的两个方程组成的方程组:
| ax1 + bx2 | = u |
| cx1 + dx2 | = v, = v, |
其中 a、b、c、d、u 和 v 是 a ≠ 0 或 c ≠ 0(或两者兼而有之)的数字,b ≠ 0 或 d ≠ 0(或两者兼而有之)。
One straightforward way to solve for x1 and x2 is to isolate one of the variables in one of the equations and substitute the result into the other equation. Suppose that d ≠ 0. Then from the second equation we have
求解 x1 和 x2 的一种简单方法是隔离其中一个方程中的一个变量,并将结果代入另一个方程。假设 d ≠ 0。然后,从第二个方程中,我们有
x2 = (v − cx1)/d.
将此表达式代入 x2 到第一个方程中得到
ax1 + b(v − cx1)/d = u,
我们可以写成
(ad − bc)x1 = du − bv.
- ad − bc ≠ 0
- We have
我们有To find x2 we use the fact that x2 = (v − cx1)/d to get
x1 = du − bv ad − bc .
为了找到 x2,我们使用 x2 = (v − cx1)/d 这一事实来得到x2 = av − cu ad − bc . - ad − bc = 0
- Given that
鉴于(ad − bc)x1 = du − bv,if du ≠ bv then the equations have no solution, and if du = bv the set of solutions is the set of pairs (x1, x2) satisfying cx1 + dx2 = v (that is, the set of pairs (x1, (v − cx1)/d) for any number x1).
(ad − bc)x1 = du − bv,
如果 Du ≠ BV,则方程没有解,如果 DU = BV,则解集是满足 Cx1 + Dx2 = V(即对集)的对集 (x1, x2) (x1, (v − cx1)/d) 对于任意数字 x1)。
In summary, the solutions of the system of equations have three possible forms.
总之,方程组的解有三种可能的形式。
- If ad ≠ bc then the equations have a unique solution,
如果 ad ≠ bc,则方程具有唯一的解,(x1, x2)
(x1、x2)= 
du − bv ad − bc , av − cu ad − bc 
. - If ad = bc and du = bv then the set of solutions of the equations is the set of pairs
如果 ad = bc 且 du = bv,则方程的解集是对的集合for any number x1.
x1, x1、 v − cx1 d 
对于任意数字 x1。 - If ad = bc and du ≠ bv then the equations have no solution.
如果 ad = bc 且 du ≠ bv,则方程没有解。
This method of isolating a variable in one equation and substituting it into another equation is cumbersome when the system consists of more than two equations and two variables. I now describe a more elegant method.
当系统由两个以上的方程和两个变量组成时,这种将变量隔离在一个方程中并将其替换为另一个方程的方法很麻烦。现在,我描述了一种更优雅的方法。
n equations in n variables
n 个变量中的 n 个方程
We can write the system of two equations in two variables in the previous section in matrix form, as
我们可以将上一节中的两个方程组用两个变量以矩阵形式写成,即
|
|
= |
|
. (*) |
n 个变量中的一般 n 方程组可以写成
Ax = b,
其中 A 是 n × n 矩阵,x 和 b 是 n × 1 列向量。
If A is nonsingular, then multiplying each side by the inverse A−1 of A yields
如果 A 是非奇异的,则将每一侧乘以 A 的倒数 A-1 得到
x = A−1b,
在这种情况下,这是唯一的解决方案。 因此,在这种情况下求解方程组相当于找到矩阵 A 的逆函数。
If the determinant of A is zero, then whether the system of equations has many solutions or none depends on the ranks of A and the augmented matrix defined as follows.
如果 A 的行列式为零,则方程组是否具有许多解,是否没有解,取决于 A 的秩和如下所示的增广矩阵。
- Definition 定义
-
Let A be an n × n matrix and b an n × 1 column vector. The augmented matrix of (A, b) is the matrix with n rows and n + 1 columns in which A constitutes the first n rows and columns and b is the last column.
设 A 是一个 n × n 矩阵,b 是一个 n × 1 列向量。(A, b) 的增广矩阵是具有 n 行和 n + 1 列的矩阵,其中 A 构成前 n 行和列,b 是最后一列。
以下结果给出了方程组 Ax = b 具有一个、多个或没有解的条件。
- Proposition 1.3.1 提案 1.3.1
-
Let A be an n × n matrix and let b be an n × 1 column vector. If A is nonsingular then the system of equations
设 A 为 n × n 矩阵,设 b 为 n × 1 列向量。 如果 A 是非奇异的,则方程组Ax = bhas a unique solution, x = A−1b. If the determinant of A is zero, then the system has infinitely many solutions if the rank of the augmented matrix of (A, b) is equal to the rank of A, and otherwise has no solution.
有一个唯一的解,x = A−1b。 如果 A 的行列式为零,则如果 (A, b) 的增强矩阵的秩等于 A 的秩,则系统具有无限多个解,否则没有解。
- Source
- For a proof, see Hadley (1961), pp. 168–169.
If n = 2 or n = 3, the inverse of A is relatively easy to compute, so that if a system of equations has a solution, this solution may easily be found, as the following examples demonstrate.
如果 n = 2 或 n = 3,则 A 的逆函数相对容易计算,因此,如果方程组有解,则很容易找到此解,如下例所示。
- Example 1.3.1 例 1.3.1
-
Consider the system of equations
考虑方程组Write it in matrix form. If ad ≠ bc then the inverse of the matrix on the left exists and isax1 + bx2 = u cx1 + dx2 = v.
以矩阵形式编写。 如果 ad ≠ bc,则左侧矩阵的逆矩阵存在并且为so we have 所以我们有1 ad − bc 
d −b 
−c a Thus 因此
x1 1 倍 
x2 2 位英雄 = 1 ad − bc 
d −b 
−c a 
u 
v . and 和x1 = ud − bv ad − bc as we found before. 正如我们之前发现的那样。x2 = va − cu ad − bc
- Example 1.3.2 例 1.3.2
-
Consider the system of equations
考虑方程组When written in matrix form Ax = b, the matrix A is2 x1 + 1 倍+ x2 + 2 倍+ 2 x3 3 位英雄 = 1 x1 − x2 + 2 倍+ x3 3 位英雄 = 0 2 x2 − x3 3 位英雄 = 3.
当以矩阵形式 Ax = b 书写时,矩阵 A 为The determinant of this matrix is 3 ≠ 0, so the matrix is nonsingular. Using the general formula for the inverse of a matrix, the inverse of the matrix is
2 1 2 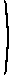
1 −1 -1 1 0 2 −1 -1 .
此矩阵的行列式是 3 ≠ 0,因此该矩阵是非奇异矩阵。 使用矩阵逆的通用公式,矩阵的逆为Multiplying this matrix by the transpose of (1, 0, 3) yields (x1, x2, x3) = (8/3, 1/3, −7/3), which is thus the unique solution of the system of equations. (By substituting this list of values into the original equations you can verify that it is indeed a solution.)
−1/3 -1/3 5/3 1 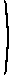
1/3 −2/3 -2/3 0 2/3 −4/3 -4/3 −1 -1 .
将此矩阵乘以 (1, 0, 3) 的转置得到 (x1, x2, x3) = (8/3, 1/3, −7/3),因此是方程组的唯一解。 (通过将这个值列表代入原始方程式,您可以验证它确实是一个解。
- Example 1.3.3 例 1.3.3
-
Consider the system of equations
考虑方程组When written in matrix form, the matrix on the left is4 x1 + 1 倍+ 2 x2 + 2 倍+ x3 3 位英雄 = 1 2 x1 − 2 x2 + 2 倍+ 2 x3 3 位英雄 = 0 4 x2 − 2 x3 3 位英雄 = 3.
当以矩阵形式编写时,左侧的矩阵为The determinant of this matrix is 0; its rank is 2. The augmented matrix is
4 2 1 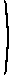
2 −2 -2 2 0 4 −2 -2 .
此矩阵的行列式为 0;它的等级是 2。 增广矩阵为This matrix has rank 3 (the determinant of the 3 × 3 matrix consisting of the last three rows and columns is 14 ≠ 0), so by the earlier result, the system of equations has no solution. (Another way to see that the system has no solution is to multiply the second equation by 2 and the third equation by 1.5 and add them together. The resulting equation is inconsistent with the first equation.)
4 2 1 1 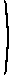
2 −2 -2 2 0 0 4 −2 -2 3 .
此矩阵的秩为 3(由最后三行和列组成的 3 × 3 矩阵的行列式为 14 ≠ 0),因此根据前面的结果,方程组没有解。 (另一种看出系统没有解的方法是将第二个方程乘以 2,将第三个方程乘以 1.5,然后相加 他们在一起。 得到的方程与第一个方程不一致。
- Example 1.3.4 例 1.3.4
-
Consider the system of equations
考虑方程组When written in matrix form, the matrix on the left is3 x1 + 1 倍+ 4 x2 2 位英雄 = 7 6 x1 + 1 倍+ 8 x2 2 位英雄 = 14.
当以矩阵形式编写时,左侧的矩阵为The determinant of this matrix is 0; its rank is 1. The augmented matrix is
3 4 
6 8 .
此矩阵的行列式为 0;它的等级是 1。 增广矩阵为This matrix has rank 1 (the determinant of every 2 × 2 submatrix is 0), so by the earlier result, the system of equations has infinitely many solutions.
3 4 7 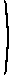
6 8 14 .
此矩阵的秩为 1(每 2 × 2 个子矩阵的行列式为 0),因此根据前面的结果,方程组具有无限多个解。The second equation is twice the first one, so any (x1, x2) that satisfies the first equation satisfies the second one. Hence (x1, x2) is a solution of the system of equations if and only if 3x1 + 4x2 = 7, or, if you like, x2 = (7 − 3x1)/4.
第二个方程是第一个方程的两倍,因此任何满足第一个方程的 (x1, x2) 都满足第二个方程。因此,(x1, x2) 是方程组的解,当且仅当 3x1 + 4x2 = 7,或者,如果你愿意,x2 = (7 − 3x1)/4。
Cramer's rule Cramer 规则
A useful implication of the fact that the solution of the system Ax = b is given by x = A−1b if A is nonsingular is the following result (due to Gabriel Cramer, 1704–1752), which gives an explicit expression for the value of each variable separately.如果 A 是非奇异的,则系统 Ax = b 的解由 x = A−1b 给出这一事实的一个有用含义是以下结果(由于 Gabriel Cramer,1704-1752),它给出了每个变量值的显式表达式 分别。
- Proposition 1.3.2 (Cramer's rule)
提案 1.3.2(克莱默规则) -
Let A be an n × n matrix, let b be an n × 1 column vector, and consider the system of equations
设 A 是一个 n × n 矩阵,设 b 是一个 n × 1 列向量,并考虑方程组Ax = bwhere x is an n × 1 column vector. If A is nonsingular then the (unique) value of x that satisfies the system is given by
其中 x 是 n × 1 列向量。 如果 A 是非奇异的,则满足系统的 x 的(唯一)值由下式给出xi = |A*(b,i)|/|A| for i = 1, ..., n,where A*(b,i) is the matrix obtained from A by replacing the ith column with b.
x = |A*(b,i)|/|A|对于 i = 1, ..., n,
其中 A*(b,i) 是通过将第 i列替换为 b 从 A 获得的矩阵。
- Proof 证明
-
We have x = A−1b, so that
我们有 x = A−1b,因此xi = ∑nwhere vij is the (i,j)th component of A−1.
j=1vijbj,
vij bj,
其中 vij 是 A−1 的第 (i,j) 个分量。Now, by a previous result, the (i,j)th component of A−1 is (−1)i+j|Aji|/|A|. Thus
现在,根据前面的结果,A-1 的 (i,j) 第 (i,j) 个分量是 (-1)i+j|Aji|/|A|。因此xi = ∑nFinally, calculate the determinant of A*(b,i) in the statement of the result by expanding along its ith column. This column is b, so according to the second part of a previous result we have
j=1(−1)i+j|Aji|bj/|A|.
(−1)i+j|Aji|bj/|A|。
最后,通过沿结果陈述的第 i列展开来计算结果陈述中 A*(b,i) 的行列式。 此列为 b,因此根据前一个结果的第二部分,我们有|A*(b,i)| = ∑n |A*(b,i)|= ∑nestablishing the result. (Note that because i is the index of the column along which we are expanding, the roles of i and j here are reversed relative to their roles in the statement of the result we are using.)
j=1(−1)i+jbj|Aji|,
(−1)i+jbj|Aji|,
建立结果。 (请注意,因为 i 是我们扩展的列的索引,所以这里 i 和 j 的角色相对于它们在我们使用的结果的语句中的角色是相反的。
- Example 1.3.5 例 1.3.5
-
Applying Cramer's rule to the system
将 Cramer 规则应用于系统if ad ≠ bc we getax1 + bx2 = u cx1 + dx2 = v, = v,
如果 ad ≠ bc,我们得到and 和x1 = 
u b 
v d ad − bc Calculating the determinants in the numerators, we havex2 = 
a u 
c v ad − bc .
计算分子中的行列式,我们有and 和x1 = ud − bv ad − bc x2 = va − cu ad − bc .
如果您只想计算方程组解中某些变量的值,则 Cramer 规则特别有用,如下例所示。
- Example 1.3.6 例 1.3.6
-
The value of x2 in a solution of the system of equations
方程组解中 x2 的值is, by Cramer's rule, the determinant of2 x1 + 1 倍+ x2 + 2 倍+ 2 x3 3 位英雄 = 1 x1 − x2 + 2 倍+ x3 3 位英雄 = 0 2 x2 − x3 3 位英雄 = 3
是divided by the determinant of
2 1 2 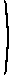
1 0 1 0 3 −1 -1
除以 的行列式The first determinant is 1 and the second is 3, so the value of x2 in the solution of the system is 1/3.
2 1 2 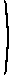
1 −1 -1 1 0 2 −1 -1 .
第一个行列式是 1,第二个行列式是 3,因此 x2 在系统解中的值为 1/3。