Polynomial Fitting – C PROGRAM
多项式拟合 – C PROGRAM

Jun 1, 2018 6月 1， 2018

Okay, so here I am sharing a code for fitting a polynomial to a given set of data-points using the Least Squares Approximation Method(Wikipedia).
好的，所以在这里我分享一个代码，用于使用最小二乘近似方法（Wikipedia）将多项式拟合到一组给定的数据点。

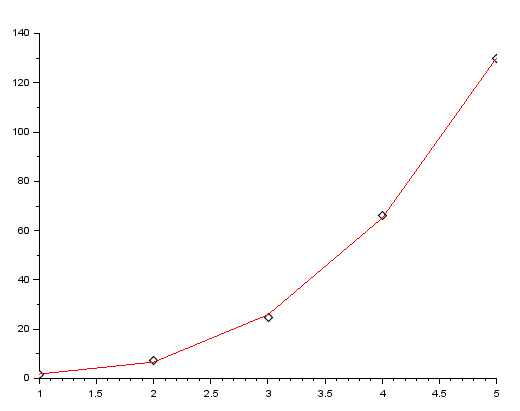
Let’s say we have $N$ data-point pairs and we are trying to fit them using a polynomial of degree $n$ . If N=n+1 then the polynomial will pass exactly through each point and it will correspond to the interpolating polynomial that I wrote about earlier.
假设我们有 $N$ 数据点对，我们试图使用多项式 $n$ 来拟合它们。如果 N=n+1，那么多项式将正好通过每个点，它将对应于我之前写的插值多项式。

Let’s say the polynomial we are using is given as:
假设我们使用的多项式为：

$a_0+a_1x+a_2x^2+a_3x^3+.....+a_nx^n$

with errors given by 给出的错误由
$e_i=Y_i-y_i=Y_i-a_0-a_1x_i-a_2x_i^2-....-a_nx_i^n$

Here, we are using $Y_i$ to represent the observed data-points corresponding to $x_i$ . We now minimize the following quantity
在这里，我们用来 $Y_i$ 表示对应于 $x_i$ 的观测数据点。我们现在最小化以下数量

$S=\Sigma_{i=1}^Ne_i^2=\Sigma_{i=1}^N(Y_i-y_i=Y_i-a_0-a_1x_i-a_2x_i^2-....-a_nx_i^n)^2$

At the minimum all the partial derivatives with respect to the coefficients will vanish. This will give us the following $n+1$ equations:
至少，所有与系数相关的偏导数都将消失。这将为我们提供以下 $n+1$ 方程式：
$\frac{\partial S}{\partial a_0}=0=\Sigma_{i=1}^N2(Y_i-a_0-a_1x_i-....-a_ix_i^n)(-1),$
$\frac{\partial S}{\partial a_1}=0=\Sigma_{i=1}^N2(Y_i-a_0-a_1x_i-....-a_ix_i^n)(-x_i),$
.
.
.
$\frac{\partial S}{\partial a_n}=0=\Sigma_{i=1}^N2(Y_i-a_0-a_1x_i-....-a_nx_i^n)(-x_i^n),$

Dividing each by -2 and rearranging gives the $n+1$ normal equations to be solved simultaneously:
将每个除以 -2 并重新排列得到要同时求解的 $n+1$ 正态方程：

$\begin{bmatrix} N& \Sigma x_i& \Sigma x_i^2& \dots& \Sigma x_i^n& \\ \Sigma x_i& \Sigma x_i^2& \Sigma x_i^3& \dots& \Sigma x_i^{n+1}& \\ \Sigma x_i^2& \Sigma x_i^3& \Sigma x_i^4& \dots& \Sigma x_i^{n+2}& \\ & \vdots& & & \vdots& \\ \Sigma x_i^n& \Sigma x_i^{n+1}& \Sigma x_i^{n+2}& \dots& \Sigma x_i^{2n}& \end{bmatrix}\begin{bmatrix} a \end{bmatrix}=\begin{bmatrix} \Sigma Y_i\\ \Sigma x_iY_i\\ \Sigma x_i^2Y_i\\ \vdots\\ \Sigma x_i^nY_i \end{bmatrix}$
where $x_i$ and $Y_i$ are the data-points entered by the user and $[a]=[a_0,a_1,..a_n]^T$ which are the required coefficients.
其中 $x_i$ 和 $Y_i$ 是用户输入的数据点， $[a]=[a_0,a_1,..a_n]^T$ 哪些是所需的系数。

So we just need to build up the above system of equations and then solve it using Gaussian elimination to get the coefficients.
因此，我们只需要建立上面的方程组，然后使用高斯消元法求解它即可得到系数。

The following program illustrates the process.
以下程序演示了该过程。

CODE: 法典：

/******************************************************
*************Chi-square fitting**************
Polynomial Fitting
******************************************************/
#include<stdio.h>
#include<math.h>
/*******
 Function that performs Gauss-Elimination and returns the Upper triangular matrix and solution of equations:
There are two options to do this in C.
1. Pass the augmented matrix (a) as the parameter, and calculate and store the upperTriangular(Gauss-Eliminated Matrix) in it.
2. Use malloc and make the function of pointer type and return the pointer.
This program uses the first option.
********/
void gaussEliminationLS(int m, int n, double a[m][n], double x[n-1]){
    int i,j,k;
    for(i=0;i<m-1;i++){
        //Partial Pivoting
        for(k=i+1;k<m;k++){
            //If diagonal element(absolute vallue) is smaller than any of the terms below it
            if(fabs(a[i][i])<fabs(a[k][i])){
                //Swap the rows
                for(j=0;j<n;j++){                
                    double temp;
                    temp=a[i][j];
                    a[i][j]=a[k][j];
                    a[k][j]=temp;
                }
            }
        }
        //Begin Gauss Elimination
        for(k=i+1;k<m;k++){
            double  term=a[k][i]/ a[i][i];
            for(j=0;j<n;j++){
                a[k][j]=a[k][j]-term*a[i][j];
            }
        }
         
    }
    //Begin Back-substitution
    for(i=m-1;i>=0;i--){
        x[i]=a[i][n-1];
        for(j=i+1;j<n-1;j++){
            x[i]=x[i]-a[i][j]*x[j];
        }
        x[i]=x[i]/a[i][i];
    }
             
}
/*******
Function that prints the elements of a matrix row-wise
Parameters: rows(m),columns(n),matrix[m][n] 
*******/
void printMatrix(int m, int n, double matrix[m][n]){
    int i,j;
    for(i=0;i<m;i++){
        for(j=0;j<n;j++){
            printf("%lf\t",matrix[i][j]);
        }
        printf("\n");
    } 
}
main(){
    //no. of data-points
    int N;  
    //degree of polynomial
    int n;  
    printf("Enter the no. of data-points:\n");
    scanf("%d",&N);
    //arrays to store the c and y-axis data-points
    double x[N], y[N];  
    printf("Enter the x-axis values:\n");
    int i,j;
    for(i=0;i<N;i++){
        scanf("%lf",&x[i]);
    }
    printf("Enter the y-axis values:\n");
    for(i=0;i<N;i++){
        scanf("%lf",&y[i]);
    }
    printf("Enter the degree of polynomial to be used:\n");
    scanf("%d",&n);
    // an array of size 2*n+1 for storing N, Sig xi, Sig xi^2, ...., etc. which are the independent components of the normal matrix
    double X[2*n+1];  
    for(i=0;i<=2*n;i++){
        X[i]=0;
        for(j=0;j<N;j++){
            X[i]=X[i]+pow(x[j],i);
        }
    }
    //the normal augmented matrix
    double B[n+1][n+2];  
    // rhs
    double Y[n+1];      
    for(i=0;i<=n;i++){
        Y[i]=0;
        for(j=0;j<N;j++){
            Y[i]=Y[i]+pow(x[j],i)*y[j];
        }
    }
    for(i=0;i<=n;i++){
        for(j=0;j<=n;j++){
            B[i][j]=X[i+j]; 
        }
    }
    for(i=0;i<=n;i++){
        B[i][n+1]=Y[i];
    }
    double A[n+1];
    printf("The polynomial fit is given by the equation:\n");
    printMatrix(n+1,n+2,B);
    gaussEliminationLS(n+1,n+2,B,A);
    for(i=0;i<=n;i++){
        printf("%lfx^%d+",A[i],i);
    }
     
}

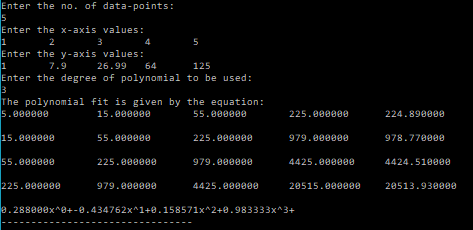
OUTPUT: 输出：

So that’s it! That’s how you perform a polynomial fit to a given set of data.
就是这样！这就是对给定数据集执行多项式拟合的方式。

Note: You can run the program yourself and verify the results here: https://www.onlinegdb.com/yd6DgVP98
注意：您可以自行运行程序并在此处验证结果：https://www.onlinegdb.com/yd6DgVP98

I had written a C++ code for this a long time ago, and coincidentally it got very popular for some reason. But then I felt the need to make an Android app that does the same.
我很久以前为此编写了 C++ 代码，巧合的是，由于某种原因它变得非常流行。但后来我觉得有必要制作一个能做到这一点的 Android 应用程序。

So I ported my code to JAVA so that it works in my Android App.
因此，我将我的代码移植到 JAVA，以便它在我的 Android 应用程序中运行。

So if you want you can check out those posts too.
因此，如果您愿意，您也可以查看这些帖子。

Hope you guys find it useful!
希望你们觉得有用！
If you have any questions/doubts, hit me up in the comments section below.
如果您有任何问题/疑问，请在下面的评论部分与我联系。

You can refer to the following links for more info:
有关详细信息，您可以参考以下链接：
Linear Fitting – Lab Write-Up
线性拟合 – 实验室报告
Linear Fitting – C++ Program
线性拟合 – C++ 程序
Linear Fitting – Scilab Code
线性拟合 – Scilab Code
Curve Fit Tools – Android App (using the above code)
Curve Fit Tools – Android 应用程序（使用上述代码）
Curve Fit Tools – Documentation
曲线拟合工具 – 文档
Curve Fit Tools – Play Store
Curve Fit 工具 – Play 商店
Curve Fit Tools – GitHub Repository
曲线拟合工具 – GitHub 存储库
Curve Fitters – Scilab Toolbox
曲线钳工 – Scilab Toolbox

Get Article as PDF
以 PDF 格式获取文章

Manas Sharma 玛纳斯·夏尔马

I’m a physicist specializing in computational material science with a PhD in Physics from Friedrich-Schiller University Jena, Germany. I write efficient codes for simulating light-matter interactions at atomic scales. I like to develop Physics, DFT, and Machine Learning related apps and software from time to time. Can code in most of the popular languages. I like to share my knowledge in Physics and applications using this Blog and a YouTube channel.
我是一名专门研究计算材料科学的物理学家，拥有德国耶拿弗里德里希-席勒大学的物理学博士学位。我编写了有效的代码，用于在原子尺度上模拟光与物质的相互作用。我喜欢不时开发与物理、DFT 和机器学习相关的应用程序和软件。可以用大多数流行的语言编码。我喜欢使用这个博客和 YouTube 频道分享我在物理和应用方面的知识。

manas.bragitoff.com/

Related 相关

Lagrange Interpolation Polynomial – C PROGRAM
拉格朗日插值多项式 – C 程序

Given a set of $latex n+1 &s=2$ data-points $latex (x_i,y_i) &s=2$ , the Lagrange Interpolating Polynomial is a polynomial of degree $latex \leq n &s=2$ , such that it passes through all the given $latex n+1 &s=2$ data-points. It is given as, $latex \boxed{Pn(x) = \sum^n_{i=0} L_i(x)y_i} &s=2$ where $latex (x_0,y_0), (x_1,y_1),.....(x_n,y_n)…

January 15, 2018 一月 15， 2018

In "C Programs" 在“C 程序”中

Polynomial Fitting – JAVA Code/Program (works on Android as well)
多项式拟合 – JAVA 代码/程序（也适用于 Android）

Okay, so the following is a code for fitting a polynomial to a given set of data using the Least Squares Approximation Method(Wikipedia). Formula Used: $latex \begin{bmatrix} N& \Sigma x_i& \Sigma x_i^2& \dots& \Sigma x_i^n& \\ \Sigma x_i& \Sigma x_i^2& \Sigma x_i^3& \dots& \Sigma x_i^{n+1}& \\ \Sigma x_i^2& \Sigma x_i^3& \Sigma…

April 4, 2017 四月 4， 2017

In "Android Studio" 在“Android Studio”中

Linear Spline – Piecewise Interpolation [C PROGRAM]
线性样条 – 分段插值 [C PROGRAM]

Lagrange or Newton polynomial interpolations are useful interpolation techniques to have in your sleeves, but they don't always give the best or desired result. As the degree of the polynomial increases, so do the wiggles. Therefore, it is often advantageous to use piecewise interpolation, also known as spline interpolation. A…

February 9, 2018 二月 9， 2018

In "C Programs" 在“C 程序”中

[wpedon id="7041" align="center"]
[wpedon id=“7041” align=“中心”]

26 thoughts on “Polynomial Fitting – C PROGRAM”
关于“多项式拟合 – C 程序”的 26 条思考

Aaron Rainey 亚伦·雷尼 February 20, 2019 二月 20， 2019

Well done, this is a bit cleaner implementation. Also, this balances out to a database implementation that I have developed.
干得好，这是一个更干净的实现。此外，这与我开发的数据库实现相平衡。

Loading... 装载。。。

Reply 答
1. Manas Sharma 玛纳斯·夏尔马 February 20, 2019 二月 20， 2019
  
  I’m glad you found it useful!
  我很高兴你发现它很有用！
  
  Loading... 装载。。。
  
  Reply 答
Rehman 拉赫曼 March 7, 2019 三月 7， 2019

I already have a couple of .dat files, and do not want to type the X and Y values, because it would take too long. Basically, let a single program give the polynomial fit equations for different sets of data.
我已经有几个.dat文件，并且不想键入 X 和 Y 值，因为这会花费太长时间。基本上，让单个程序给出不同数据集的多项式拟合方程。

Loading... 装载。。。

Reply 答
1. Manas Sharma 玛纳斯·夏尔马 March 7, 2019 三月 7， 2019
  
  That’s extremely easy. 这非常容易。
  Just add a few lines.
  只需添加几行即可。
  If you’re looking for some code go through some codes on this blog, for ex: plotting exercises
  如果您正在寻找一些代码，请查看此博客上的一些代码，例如：绘图练习
  
  Loading... 装载。。。
  
  Reply 答
Eric 埃里克 April 11, 2019 四月 11， 2019

Thanks for leading me here, this is quite handy! So I am still trying to incorporating weights to perform a weighted least squares fit. Considering the theoretical equation I would incorporate the weight in the following position as ‘w’:
谢谢你把我带到这里，这很方便！因此，我仍在尝试合并权重以执行加权最小二乘拟合。考虑到理论方程，我会将以下位置的权重合并为“w”：

Y[i]=Y[i]+ w * pow(x[j],i)*y[j];
Y[i]=Y[i]+ w * pow（x[j]，i）*y[j];

Since their it should be reside after the derivations.
由于它们应该驻留在派生之后。

Thank you in advance for you input!
提前感谢您的输入！

Greetings 问候
Eric 埃里克

Loading... 装载。。。

Reply 答
1. Randy 兰迪 April 17, 2020 四月 17， 2020
  
  Hi Eric, 嗨，埃里克，
  I’m looking at doing the same thing, weighted LS fit. Did you ever try this? Do you have hints?
  我正在考虑做同样的事情，加权 LS 拟合。你试过这个吗？你有提示吗？
  Thanks, 谢谢
  Randy 兰迪
  
  Loading... 装载。。。
  
  Reply 答
Avinash 阿维纳什 June 5, 2019 六月 5， 2019

Wonderful program! It just worked without any problems.
精彩的节目！它只是没有任何问题。
And the explanation too is really easy to understand.
解释也很容易理解。
Greetings,
Avinash

Loading...

Reply
1. Manas Sharma June 5, 2019
  
  Thanks!
  
  Loading...
  
  Reply
Rajeev September 20, 2019

Hello Manas,

can you share a surface fit polynomial c/c++ code or the logic to write one?

Thanks,
Rajeev

Loading...

Reply
Sanjeev October 14, 2019

Hello Manas,
I am trying to write a linear surface fit algorithm f(x,y)=A+Bx+Cy+Dxy+Ex^2……..; having the order of 3, 4; 4, 4 and/or 4, 3; Can you suggest me how does the augmented matrix looks like? what is the best approach to get PseudoInverse? what changes to the above code, I should be doing to address a surface fit on z; Any pointers would be much appreciated.

Loading...

Reply
JAroslav Hook October 8, 2020

I do not think you even compiled it
a) gaussEliminationLS(int m, int n, double a[m][n], double x[n-1])
<== cannot have variable array sizez

b) Y[i]=Y[i]+pow(x[j],i)*y[j];<== 'y' is not even declared

c) indecis i,j are not declared anywhere …

Loading...

Reply
1. Manas Sharma October 27, 2020
  
  These do work on certain compilers. For example if you use Dev C++ it will run guaranteed.
  
  Loading...
  
  Reply
  1. Sten Odenwald January 27, 2021
    
    No it doesnt….I compiled it with Dev C++ which I installed last month and it fails just like Hook says….plus you did not answer Hooks questions about how to fix this problem.
    
    Loading...
    
    Reply
    1. Manas Sharma March 19, 2021
      
      You’ve got to be blind if you cannot see the indices i and j being declared. Secondly, not only is y[N] declared, it is also explained what it is with a comment. Y[n+1] is the RHS of the ‘normal’ system of equations.
      
      I didn’t explain because there was nothing to explain. I will make a video of me running it in DevC++ if you can give me a proper error that you get. You just say that it fails. Can’t you give the error you get? How can I help with you just the information you give.
      
      Loading...
      
      Reply
JAroslav Hook October 8, 2020

It does not even compile

a) cannot declare the variable array size like function (m,n, a[m][n] ..)
b) indecis i,j are never declared
c) “y” is not declared ( should be capital Y

Loading...

Reply
Ron Zoest June 2, 2021

Hi Manas
Thanks for the code I have adapted this and have it running VS 2019 as a C++ program. I made the some changes to make it run properly they are:
//arrays to store the c and y-axis data-points
//double x[N], y[N];
double* x = new double[N];
double* y = new double[N];
this needs to be done for all single dimensioned arrays.

he following change is needed for 2 dimensional arrays:
//the normal augmented matrix
// double B[n + 1][n + 2];
double** B = new double* [n + 1];
for (int i = 0; i < n + 1; i++)
B[i] = new double[n + 2];
Then when passing the arrays as parameters to the functions the following changes are required.
void gaussEliminationLS(int m, int n, double **a, double *x) {
void printMatrix(int m, int n, double **matrix) {
Also the compiler doesn't like scanf this needs to be replaced with scanf_s
Then it will build with out errors.
Note many compilers do not handle dynamic arrays, but most will allow the changes I have made. It seem that some of the above commenters don't understand how to create dynamic arrays in C++.

Loading...

Reply
1. Manas Sharma June 2, 2021
  
  Hi, Thanks a lot for your efforts. I am sure these would be helpful for others. What you say is correct about arrays. But I still think that a lot of compilers can run this code contrary to what the others have pointed out above.
  
  For example you can even run it online:
  https://onlinegdb.com/yd6DgVP98
  
  Loading...
  
  Reply
  1. Ron Zoest June 2, 2021
    
    Hi Manas
    You are correct I have just tried this on my personal PC using the gcc compiler version 8.3.0 an d it compiles and runs exactly as you show. This shows that the open source is often ahead of proprietary compiler.
    Regards
    Ron
    
    Loading...
    
    Reply
Brandon Blackburn November 19, 2021

This is amazing! I’ve been looking for a way to use polynomial regression for my capstone project. Would it be okay with you if I use this code to analyze a dataset based on Google PlayStore apps? Thank you!

Loading...

Reply
chihohong May 6, 2022

Hi, I’m from south korea.
I was impressed with your research and it helped me a lot.
In case of overfitting, what part of the code above can be modified?

Loading...

Reply
Tamal Pal September 26, 2022

Hi Manas, This code is extremely useful for me. Can you write a code on curve fitting using any equation?

Thanks a lot

Tamal Pal

Loading...

Reply

Hi and greetings from Finland, ;>)
I’m old engineer with some programming background and I remember having
this solution using HP 9816 technical workstation running basic.
I used it for solving many given tables to formulas in my work. Now I have a
a new table to be solved, but the code has vanished.
Here I found this, which you have written in C++. I know some of C, but
this is new to me. Have you written it in VisualBasic, so that I
could port it to my Excell app+ ??
BR Matti

Unfortunately, I have no experience with Visual Basic. Fortunately, ChatGPT exists, so you can use that to port the code. Here is what I got:

Please note: It is prone to making mistakes, so you would need to spend some time debugging. I haven’t checked the code and I don’t even know how to run it.

‘******************************************************
‘*************Chi-square fitting**************
‘Polynomial Fitting
‘******************************************************

Module Module1

'Function that performs Gauss-Elimination and returns the Upper triangular matrix and solution of equations:
'There are two options to do this in C.
'1. Pass the augmented matrix (a) as the parameter, and calculate and store the upperTriangular(Gauss-Eliminated Matrix) in it.
'2. Use malloc and make the function of pointer type and return the pointer.
'This program uses the first option.
Sub gaussEliminationLS(m As Integer, n As Integer, a(,) As Double, x() As Double)

    Dim i, j, k As Integer

    For i = 0 To m - 2
        'Partial Pivoting
        For k = i + 1 To m - 1
            'If diagonal element(absolute vallue) is smaller than any of the terms below it
            If Math.Abs(a(i, i)) < Math.Abs(a(k, i)) Then
                'Swap the rows
                For j = 0 To n - 1
                    Dim temp As Double
                    temp = a(i, j)
                    a(i, j) = a(k, j)
                    a(k, j) = temp
                Next
            End If
        Next
        'Begin Gauss Elimination
        For k = i + 1 To m - 1
            Dim term As Double = a(k, i) / a(i, i)
            For j = 0 To n - 1
                a(k, j) = a(k, j) - term * a(i, j)
            Next
        Next
    Next

    'Begin Back-substitution
    For i = m - 1 To 0 Step -1
        x(i) = a(i, n - 1)
        For j = i + 1 To n - 2
            x(i) = x(i) - a(i, j) * x(j)
        Next
        x(i) = x(i) / a(i, i)
    Next

End Sub

'Function that prints the elements of a matrix row-wise
Sub printMatrix(m As Integer, n As Integer, matrix(,) As Double)
    Dim i, j As Integer
    For i = 0 To m - 1
        For j = 0 To n - 1
            Console.Write(matrix(i, j) & vbTab)
        Next
        Console.WriteLine()
    Next
End Sub

Sub Main()
' No. of data-points
Dim N As Integer
' Degree of polynomial
Dim n As Integer

Console.WriteLine("Enter the no. of data-points:")
N = Console.ReadLine()

' Arrays to store the c and y-axis data-points
Dim x(N - 1) As Double
Dim y(N - 1) As Double

Console.WriteLine("Enter the x-axis values:")
For i As Integer = 0 To N - 1
    x(i) = Console.ReadLine()
Next

Console.WriteLine("Enter the y-axis values:")
For i As Integer = 0 To N - 1
    y(i) = Console.ReadLine()
Next

Console.WriteLine("Enter the degree of polynomial to be used:")
n = Console.ReadLine()

' An array of size 2*n+1 for storing N, Sig xi, Sig xi^2, ...., etc. which are the independent components of the normal matrix
Dim X(2 * n) As Double

For i As Integer = 0 To 2 * n
    X(i) = 0
    For j As Integer = 0 To N - 1
        X(i) = X(i) + Math.Pow(x(j), i)
    Next
Next

' The normal augmented matrix
Dim B(n, n + 1) As Double
' rhs
Dim Y(n) As Double

For i As Integer = 0 To n
    Y(i) = 0
    For j As Integer = 0 To N - 1
        Y(i) = Y(i) + Math.Pow(x(j), i) * y(j)
    Next
Next

For i As Integer = 0 To n
    For j As Integer = 0 To n
        B(i, j) = X(i + j)
    Next
Next

For i As Integer = 0 To n
    B(i, n + 1) = Y(i)
Next

Dim A(n) As Double

Console.WriteLine("The polynomial fit is given by the equation:")
PrintMatrix(n + 1, n + 2, B)
gaussEliminationLS(n + 1, n + 2, B, A)

For i As Integer = 0 To n
    Console.Write("{0}x^{1}+", A(i), i)
Next

End Sub

Here is a version generated completely by ChatGPT without using my input

Public Class Form1 Private Sub btnFit_Click(sender As Object, e As EventArgs) Handles btnFit.Click ' Input data Dim xVals() As Double = {1, 2, 3, 4, 5, 6} Dim yVals() As Double = {1.2, 1.5, 1.8, 2.1, 2.4, 2.7}


    ' Degree of polynomial
    Dim degree As Integer = 2

    ' Fit polynomial
    Dim coefficients() As Double = FitPolynomial(xVals, yVals, degree)

    ' Output coefficients
    txtOutput.Text = ""
    For i As Integer = 0 To degree
        txtOutput.Text &= "a" & i & " = " & coefficients(i) & vbCrLf
    Next
End Sub

Private Function FitPolynomial(xVals() As Double, yVals() As Double, degree As Integer) As Double()
    ' Build matrix of system of equations
    Dim n As Integer = xVals.Length
    Dim matrix(n - 1, degree + 1) As Double
    For i As Integer = 0 To n - 1
        Dim x As Double = xVals(i)
        Dim y As Double = yVals(i)
        For j As Integer = 0 To degree
            matrix(i, j) = Math.Pow(x, j)
        Next
        matrix(i, degree + 1) = y
    Next

    ' Solve system of equations using Gauss-Jordan elimination
    For k As Integer = 0 To degree
        Dim maxRow As Integer = k
        For i As Integer = k + 1 To n - 1
            If Math.Abs(matrix(i, k)) > Math.Abs(matrix(maxRow, k)) Then
                maxRow = i
            End If
        Next
        If maxRow <> k Then
            For j As Integer = k To degree + 1
                Dim temp As Double = matrix(k, j)
                matrix(k, j) = matrix(maxRow, j)
                matrix(maxRow, j) = temp
            Next
        End If
        For i As Integer = k + 1 To n - 1
            Dim factor As Double = matrix(i, k) / matrix(k, k)
            For j As Integer = k To degree + 1
                matrix(i, j) -= factor * matrix(k, j)
            Next
        Next
    Next
    Dim solution(degree) As Double
    For i As Integer = degree To 0 Step -1
        Dim sum As Double = matrix(i, degree + 1)
        For j As Integer = i + 1 To degree
            sum -= matrix(i, j) * solution(j)
        Next
        solution(i) = sum / matrix(i, i)
    Next
    Return solution
End Function

End Class

fritz sonnichsen August 1, 2023

Thanks for the straightforward code. I tested it against my routines for base lining spectra and it works well. I ran it against 200 spectral points with sharp peaks at O(6). I find round off error is problematic with the coefficients spanning around 10**12. Adding the “.15” designator on the printf output gives enough decimal places to do the job.
printf( “%+.15lf*x^%d “, A[i],i);

thanks again
Fritz

Loading...

Reply
1. Manas Sharma August 13, 2023
  
  Thanks a lot for the helpful suggestion!
  This was never a production-quality code so there might be such oversights that would need to be sorted by the users.
  I had written these codes during my bachelor’s and master’s for assignments, but somehow they got a lot of views.
  
  Maybe when I find time in the future I will try to improve them.
  
  Loading...
  
  Reply